【LeetCode_15】——三数之和

今天做了力扣中的一道经典题：三数之和。这题思路倒是很快想到，调逻辑可把我调得够呛，这也正说明我的刷题思维远远不够，比起我室友半个月刷300多题的思维差远了。。。革命尚未成功，同志仍需努力。

原题链接：15. 三数之和 - 力扣（LeetCode） (leetcode-cn.com)

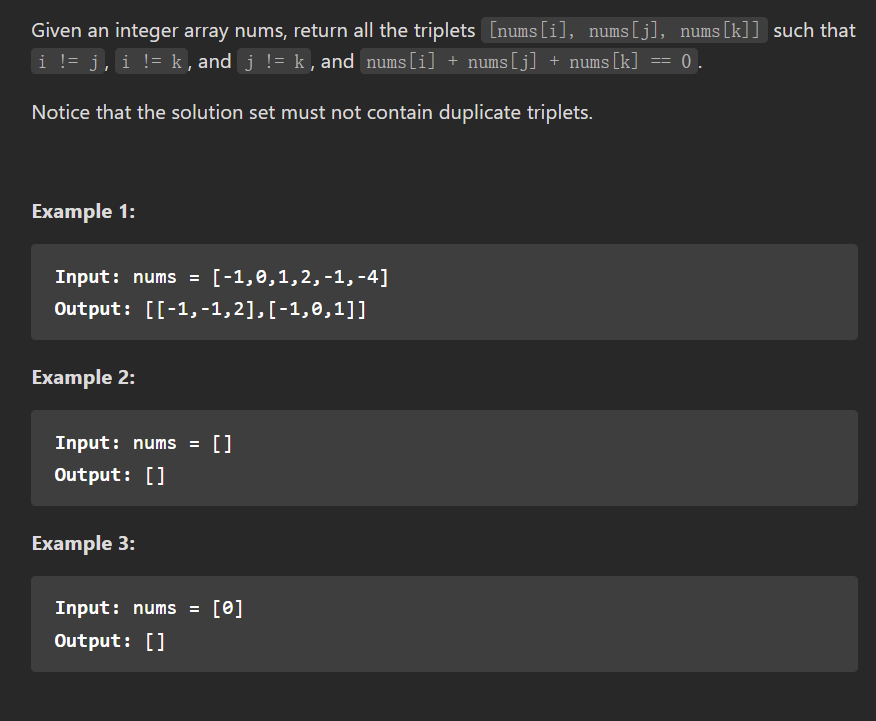
题解：题目要我们找到所给数组中所有和为0且不重复的三元数组。

由于题目中所给的数组长度不超过3000，所以最后的算法O(n²)也是可以接受的。数据最大值为1e5，也不用开long long。

如果直接枚举所有的情况，首先在时间复杂度上就无法接受：枚举所有情况需要三重循环，时间复杂度会达到O(n³)。并且暴力枚举的情况复杂，代码量也不小，很麻烦，所以我们要从题中寻找突破口。

题中的关键点在于：nums[i]+nums[j]+nums[k]=0。假设三个元素分别为a,b,c。这就意味着a，b，c三个数不全为正或负，必然有正有负。不妨假设a<=b<=c，那么a必然为负。因此，我们就可以在小于0的范围内枚举a，在大于a的情况下枚举b和c满足a+b+c=0即可。这样可以提升算法的效率，减少不必要的搜索。

根据我们上面的思路，不难发现要想轻松实现需要将数组排序，然后在小于0的范围内根据每一个a来在大于a的范围内枚举b和c。这是b和c的情况就是两数之和的情况了，因为数组已经有序，我们可以使用双指针的方法来解决此问题。

还有最重要的一点：去重，题目中要求不重复的三元组，因此在枚举的过程中我们需要去掉重复的情况。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> ans;
        int n=nums.size();
        if(n<3) return {};
        sort(nums.begin(),nums.end());
        int f,s,t;
        for(f=0;f<n-2;f++){ //f的范围只到n-3
            if(nums[f]>0) return ans;
            if(f>0&&nums[f]==nums[f-1]) continue; //去掉a的重复元素
            s=f+1;
            t=n-1;
            while(s<t){
                if(nums[f]+nums[s]+nums[t]==0){
                    vector<int> res={nums[f],nums[s],nums[t]};
                    ans.emplace_back(res);
                    s++;t--;
                    while(s<t&&nums[s]==nums[s-1]) s++; //去掉b的重复元素
                    while(s<t&&nums[t]==nums[t+1]) t--; //去掉c的重复元素
                }
                if(nums[f]+nums[s]+nums[t]>0){
                    t--;
                }
                if(nums[f]+nums[s]+nums[t]<0){
                    s++;
                }
            }
        }
        return ans;
    }
};

时间复杂度：O(N²) 

__EOF__

本文作者：天涯海角寻天涯
本文链接：https://www.cnblogs.com/yjx-7355608/p/15976811.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！