【LeetCode学习心得】运用递归解决二叉树有关问题

二叉树作为一种十分重要的数据结构，其天然的递归性质使得在解决有关二叉树的问题时可以使用递归的方法。递归是解决树的有关问题的最有效和最重要的方法之一。

在开始前，我们先来回顾一下有关递归（recurve）的概念：

数学以及程序设计方法中为递归下的定义是：若一个对象部分地包含它自己，或用它自己给自己定义，则称这个对象是递归的；若一个过程直接地或间接地调用自己，则称这个过程是递归的过程。

在以下三种情况下，常常要用到递归的方法：

1.定义是递归的，例如在求解n！或者斐波拉契数列时；

2.数据结构是递归的，例如树，链表等；

3.问题的解法只能是递归：最典型的为Tower of Hanio。

在使用递归的方法解决问题前，我们需要清楚三点：

（1）对于一个较为复杂的问题，如果能够分解成几个相对简单的且解法相同或类似的子问题时，只要解决子问题，那么原问题便可迎刃而解；

（2）当分解后的子问题可以解决时，就停止分解。我们可以说我们获得了原子问题，也就是递归结束条件。例如在求解n！时，当分解到0！=1时我们便可停止分解，0！=1就是这个递归的递归结束条件。

（3）递归定义的函数可以直接编程求解，递归过程直接反应函数的结构。

 

现在，我们来看看二叉树的递归解法中常用的两种方法：

I.“自顶向下”的解决方案

“自顶向下”的方案的思想类似于二叉树的前序遍历：在每层递归中，我们首先访问根节点来获取我们需要的信息，并将这些信息传递给下一层的子结点。

其思想可近似为：

1.考虑边界点，一般为root是nullptr的时候；

2.对当前根节点进行处理，获取信息，取得递归结束条件；

3.调用自身，进行递归；

II."自底向上"的解决方案：

“自底向上”方案思想类似于二叉树的后序遍历：在每层的递归中，我们通过对子节点调用递归函数，然后根据返回值和节点本身找到答案。

通常， “自底向上” 的递归函数 bottom_up(root) 为如下所示：

1. return specific value for null node
2. left_ans = bottom_up(root.left)            // call function recursively for left child
3. right_ans = bottom_up(root.right)        // call function recursively for right child
4. return answers                           // answer <-- left_ans, right_ans, root.val

当我们在遇到树的有关问题时，先思考：我们能否从根节点获取我们想要的信息，然后从子节点上找到问题的答案；如果行，我们就可以采用自顶向下的方式来解决问题。

如果我们能从子节点找到根节点的答案，我们就可以使用自底向上的方案来解决问题。

一个例题：（题目源自LeetCode）

二叉树的最大深度

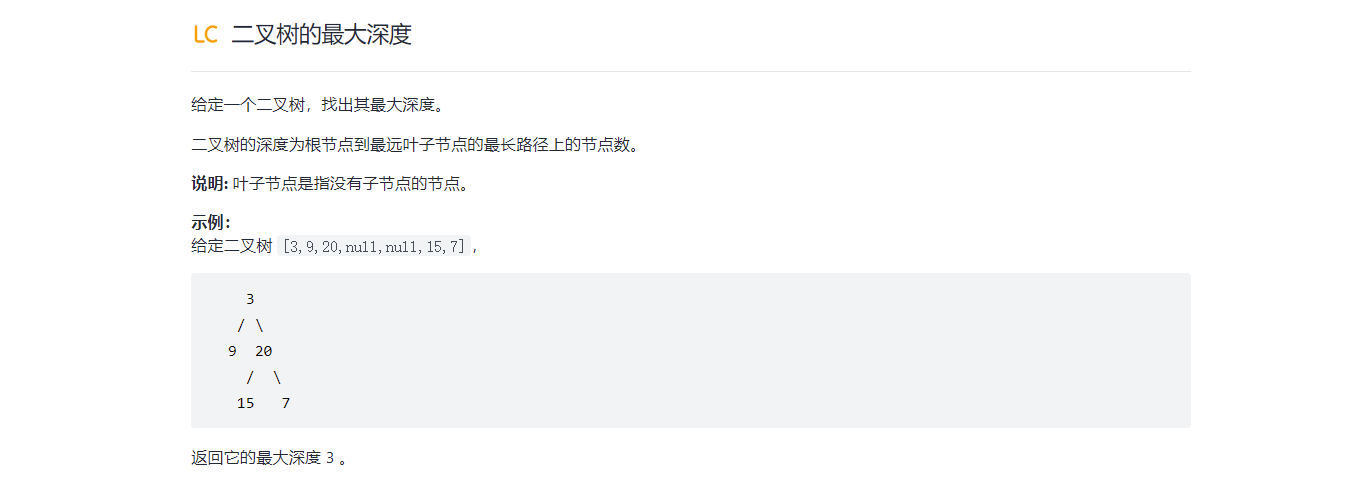
思想：当形参root为空时，其高度为零，于是我们便可将递归到一个空结点作为递归结束条件；

再分别对根节点的左子树和右子树进行递归，计算其高度；（注意+1，否则输出会为零）

最后返回左子树和右子树中较大的那个值即可；

源代码：

struct TreeNode {
  int val;
  TreeNode *left;
  TreeNode *right;
  TreeNode() : val(0), left(nullptr), right(nullptr) {}
  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==NULL) return 0;
        int maxLeft=maxDepth(root->left)+1;
        int maxRight=maxDepth(root->right)+1;
        return maxLeft>=maxRight?maxLeft:maxRight;
    }

能灵活运用递归解决树的有关问题并不容易，需要多加练习；