self-attention 前置基础知识

1. 向量的内积是什么，如何计算，最重要的，其几何意义是什么
2. 一个矩阵 W 与其自身的转置相乘，得到的结果有什么意义？

1.1 向量的内积
向量的内积是定义在两个向量之间的运算，用来计算两个向量的相似程度或者他们之间的角度关系

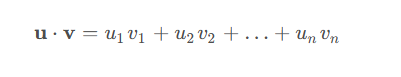
向量的结果是一个数而不是向量

1.2 向量内积的几何意义
① 两个向量的内积与他们之间的角度的余弦值成正比，aka通过向量的内积可以计算出他们之间的夹角

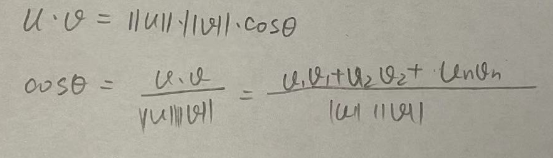
以图中这两个向量为例 u=（1,1）和 v=（1,2）

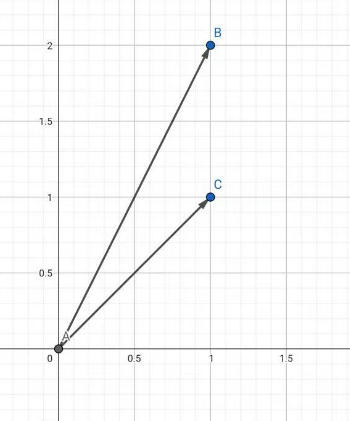
u * v = 1 * 1+1 * 2=3
两个向量之间的夹角为：
cosθ = 3/(√5 * √2 ) = 0.948683298
arccos 0.948683298 = 18.43494883

验证夹角是否是18.43494883度：
arccos (1/√5) = 63.4349879
63.4349879 - 45 = 18.4349879 ≈ 18.43494883

故通过向量内积可以得出向量之间的夹角

② 一个向量在另一个向量方向上的投影可以通过计算内积得到

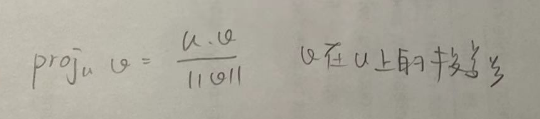
2. 矩阵与自身转置相乘的意义
   

得到的矩阵的每一个元素是矩阵对应行列的内积的结果