强化学习之一. 策略梯度 (PG)： 连续动作拒绝眨眼补帧

强化学习之一. 策略梯度 (PG)： 连续动作拒绝眨眼补帧

强化学习通过学习任务可以分为模型学习、值函数学习和策略学习。模型学习，也称基于模型的方法（Model-based Method），是指在和环境的交互过程中会对环境进行建模，可以将学习任务转化成规划任务，也就是说在学习的过程中，会形成一个对环境的想象和模拟。值函数学习不会对环境建模，直接学习值函数，所以也叫无模型方法（Model-free Method），值函数学习会记录什么时候做什么事对后面的影响是多少。策略学习也是无模型方法，不会对环境建模，也不会对值函数学习，它不会想象环境是什么样的，也不会记录行为的优劣，而是通过与环境交互直接学习一套策略，一套行为行为指南，上面写着什么时候该做什么事。

值函数学习的一些问题：

1. 无法处理连续动作。在值函数学习，例如DQN(deep Q-learning)强化学习方法中，通过建立神经网络对态进行模拟，从而使状态空间连续，不再需要更新一张冗杂的Q表（Q-table）。但是，其能选择的动作仍然离散的，比如在十字路口只能选择前后左右四个方向，但是在很多现实问题中，有很多情况需要有连续的动作，细微的动作，例如在踩刹车的时候，力道和时间都是一个连续控制，在面对此类问题时，值函数学习就会难以解决。注意：策略函数是可以处理连续问题，但是并不是只能处理连续动作，策略函数同样也可以表示离散动作。
2. 无法解决随机策略问题。值函数学习方法通常是确定性策略，因为都需要用GPI框架进行优化，在GPI框架中，agent在学习时总会选择当前价值最大的一个行为，而对于某些环境，随机策略才是最优策略，此时的值函数学习就会失效。

一.策略近似

策略学习指的就是在学习的过程中，通过与环境进行交互，不断改变做出各动作的概率，也就是好的动作就提高一点概率，坏的动作就降低一点。

类似在值函数学习中引入神经网络对值函数进行近似，在策略学习中，想要处理连续动作问题，就要对动作空间进行连续化。具体如下图

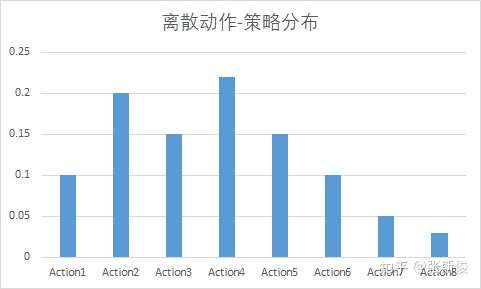
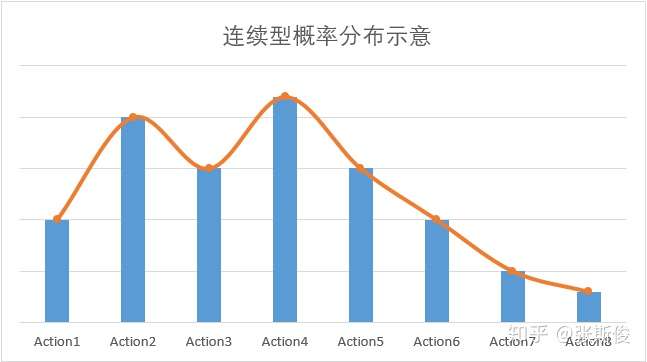
左图为一个离散的策略，高度表示当前状态下执行动作的概率，例如\(\pi(Action1|s)=0.1\) , \(\pi(Action2|s)=0.2\). 右图表示用神经网络将其连续化，这样就可以知道某些中间动作，例如\(\pi(Action1.5|s)\)的值，也就实现了动作的连续化。假设原先的策略为\(\pi(a|s)\)，用\(\theta\)表示神经网络的参数，则可以用神经网络 \(\pi _\theta(a|s)\) 近似策略 \(\pi(a|s)\)，即如下式

\[\pi(a|s)\approx\pi_\theta(a|s) \]

二.策略函数设计

我们知道策略函数表示的是在当前状态下各动作的概率，在概率论里面也叫分布函数。策略函数是一个含参表达式\(f(\theta)\)，其中 \(\theta\) 表示一系列需要训练的参数，而函数形式也有一些常用的函数，类似拟合数据时有多形式拟合也有最小二乘拟合一样。当前最常用的策略函数为softmax策略函数 和高斯策略函数，分别适用离散动作和连续动作。提示：无论什么形式都满足归一化条件\(\int\pi(a|s)da=1\)或者\(\sum_{a}\pi(a|s)=1\)，也就是所有的动作概率加起来为1

softmax策略函数有如下形式

\[\pi_\theta(s,a_n)=\frac{e^{\phi(s,a_n)^T\theta}}{\sum_{a_m} e^{\phi(s,a_m)^T\theta}} \]

其中\(\phi(s,a)\)用于表述状态和行为特征，参数\(\theta\)来为调节各行为发生的概率。

高斯概率函数为

\[\pi_\theta(a|s)\sim\mathbb{N}(\phi(s)^T\theta,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}{\rm exp}(-\frac{(a-\phi(s)^T\theta)^2}{2\sigma^2}) \]

三.优化目标函数

学习中要对策略网络进行优化，就要设立一个优化目标，这个优化目标是用来衡量当前策略的好坏的一个标准，自然地，这个优化目标会与收获reward有关。

当前有三种优化目标：

初始状态的平均收获

\[R_1(\theta)=V_{\pi_\theta}(s_1)=\mathbb{E}_{\pi_\theta}(G_1) \]

其中\(\mathbb{E}_{\pi_{\theta}}(x)\)表示的是对策略函数的分布下对\(x\)取平均，离散可以表示为\(\mathbb{E}_{\pi_{\theta}}(x)=\sum_{a}\pi(a|s)x\)，连续为积分 \(\mathbb{E}_{\pi_{\theta}}(x)=\int_a\pi(a|s)da\)

状态平均奖励

\[\bar R_S(\theta)=\sum_sd_{\pi_\theta}(s)V_{\pi_\theta}(s) \]

其中 \(d_{\pi_\theta}(s)\)表示的基于 \(\pi_\theta(a|s)\)的马尔科夫链的关于状态的静态分布，可以简单理解为它是一个态分布，但是是根据策略函数得出的

动作平均奖励

\[\bar R_A=\sum_sd_{\pi_\theta}(s)\sum_a\pi(a|s)R^a_s \]

这个动作平均奖励可以由状态价值函数和动作价值函数的关系得到 \(V(s)=\sum_a\pi(a|s)R_s^a\)，\(R_s^a\)表示在 s 状态下进行动作 a 的奖励。动作平均奖励是用的比较多的价值函数，下面我们也将以此为基础推导一下其梯度的具体表达形式。

四.目标函数梯度推导

在训练时，需要以平均奖励的最大化为目标，所以也就通过梯度上升（Gradient Ascend）的方法通过调整 \(\theta\) 对平均奖励函数进行优化，可以表示为迭代式

\[\theta' = \theta +\alpha\nabla\bar R \]

其中 \(\alpha\) 为更新步长，在学习算法中也叫学习率（Learning Rate）。在 TensorFlow 和 PyTorch 中都有已有的优化器来进行迭代优化，在调用时只需要给定目标函数 \(\bar J\) 和 学习率 \(\alpha\) 即可计算上式。但是目前 \(\bar J\) 的形式未知，需要推导。

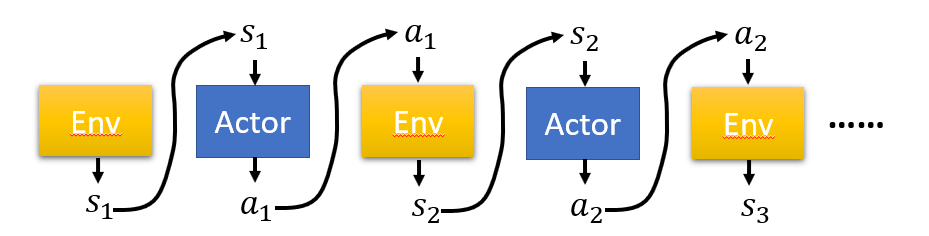
上图表示一般学习算法中的交互过程，有Env和Actor两个角色。Actor 是用来给出动作的神经网络，它的输入状态输出是动作；Env是环境，输入的是动作，输出的是状态。一般的交互过程为，首先初始化一个状态 \(s_1\) ，这个 \(s_1\) 可以是环境给定也可以是自由给定，已知 \(s_1\)， Actor根据目前策略 \(\pi_\theta\) 给出动作 \(a_1\)。给定动作 \(a_1\) 环境给出 \(s_2\) ，根据 \(s_2\) Actor 给出\(a_2\) ...以此类推。最终得到一系列状态和动作，我们包含这些状态和动作的集合称为一次轨迹（Trajectory），训练过程中需要 \(N\) 条这样的轨迹，第 \(\tau\) 条轨迹表示为

\[\tau=\{s_1,a_1,s_2,a_2,,..,s_T,a_T\} \]

​ 其中下标 \(T\) 表示在第 \(\tau\) 条轨迹中，Actor与Env交互了 \(T\) 次，而出现这条轨迹的“概率”就是一系列状态和动作出现的概率对于\(t=1\)到\(t=T\) 的积

\[\begin{align} P_{\theta,\tau}=&P(s_1)P(a_1|s_1)P(a_1|s_1,s_2)P(a_2|s_2)...\\ =&P(s_1)\prod_{t=1}^TP_\theta(a_t|s_t)P(s_{t+1}|s_t,a_t)\\ =&P(s_1)\prod_{t=1}^T\pi_\theta(a_t|s_t) P(s_{t+1}|s_t,a_t) \end{align}\tag{1} \]

其中 \(P(s_{t+1}|s_t,a_t)\)表示 \(s_t\) 态下做出动作 \(a_t\) 得到 \(s_{t+1}\) 的概率，这一概率体现的是模型性质。一般情况下为1；\(P(s_1)\) 表示选到 \(s_1\) 作为初始态的概率，初态在实际中直接指定，所以也为1。式（1）就变为

\[P_{\theta,\tau} =\prod_{t=1}^T\pi_\theta(a_t|s_t)\tag{2} \]

在一条轨迹中，Actor做出了一系列动作，在和环境交互的过程中每一步都会得到收获 \(r_t\) ，总的收获为每一步收获的求和

\[R_\tau=\sum_{t=1}^Tr_t \]

同样地，下标 \(\tau\) 表示第 \(\tau\) 条轨迹。因为每次的轨迹不同，共有 \(N\) 条轨迹，所以平均收获需要对所有的轨迹求平均

\[\bar R_\theta = \sum_\tau R_\tau P_{\theta,\tau}=\mathbb{E}_{\tau\sim\pi_\theta}[R_\tau]\ \]

也就是，每条轨迹出现的概率 \(P_{\theta,\tau}\) 乘以 这条轨迹的总收获 \(R_\tau\)，最后再求和。据此，平均收获的梯度为

\[\begin{align} \nabla \bar R_{\theta}=&\sum_\tau R_\tau \nabla P_{\theta,\tau}=\sum_\tau R_\tau P_{\theta,\tau}\nabla {\rm log}P_{\theta,\tau}\\ =& \mathbb{E}_{\tau\sim \pi_\theta}[R_\tau\nabla {\rm log} P_{\theta,\tau}] \end{align} \]

其中用到微分关系 \(\nabla f(x)=f(x)\nabla {\rm log}f(x)\) 和表示形式 \(\mathbb{E}_{x\sim p(x)}[f(x)]=\sum_xf(x)p(x)\)。实际应用中，不可能对所有 \(\tau\) 穷尽，所以可以用有限次 的平均去近似

\[\begin{equation} \nabla \bar R_{\theta}=\mathbb{E}_{\tau\sim \pi_\theta}[R_\tau\nabla {\rm log}P_{\theta,\tau}]\approx \frac{1}{N}\sum_{\tau=1}^N R_\tau \nabla {\rm log}P_{\theta,\tau} \end{equation} \]

将式（2）带入得：

\[\nabla \bar R_{\theta}\approx\frac{1}{N}\sum_{\tau=1}^N\sum_{t=1}^T R_\tau \nabla {\rm log}\pi_\theta(a_{\tau,t}|s_{\tau,t})\tag{3} \]

也就是，在 \(\tau\) 回合，做出所有动作的概率的对数 乘以 这一回合的总收获，再对所有回合求和即可得\(\nabla \bar R_{\theta}\)

五.Baseline & Advantage Function

1.设置baseline。PG(Policy Gradient)可以在两方面改进，首先根据式（3），如果环境做给的收获一直为正，那么平均收获的梯度可能也都是为正，如果采样数据够多，这没有问题。

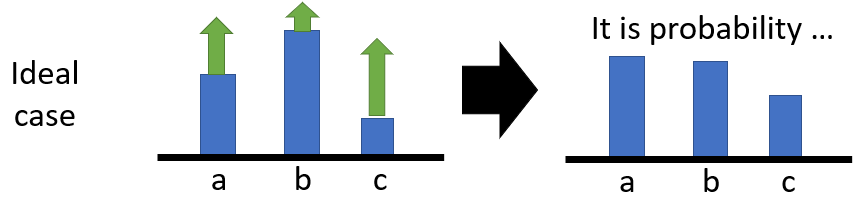
如上图，根据梯度上升，所有的动作的概率都会上升，最后归一化之后仍然得到改变后的更新后的策略。

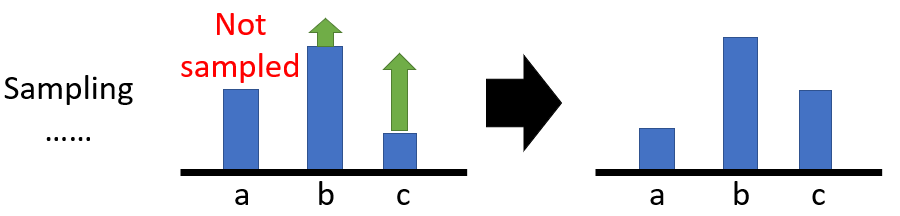
但是如果某一个动作始终没有被采样到，那么它的概率就不会得到更新，就会造成不动则降的结果，这显然不符合更新要求，所以引入一个baseline 对总收益相减一个常数，则这种情况就会避免：

\[\nabla \bar R_{\theta}\approx\frac{1}{N}\sum_{\tau=1}^N\sum_{t=1}^T (R_\tau -b) \nabla {\rm log}\pi_\theta(a_{\tau,t}|s_{\tau,t})\tag{3} \]

在实际计算的过程中，\(b\)可以选择为平均的收益\(\mathbb{E}(R_\tau)\)。

2.设置Advantage function。在式(3)中，在计算梯度的时候是将整个\(\tau\) 轨迹的所采样到的动作 \(a_{\tau,t}\) 都赋予相同的权重 \(R_\tau-b\)，这其实是不公平的。因为在 \(R_\tau\) 代表的是整个轨迹 \(\tau\) 的总收益，但是轨迹中的动作并不是全部都是正确的，所以赋予相同的权重是不合理的。例如下图左图

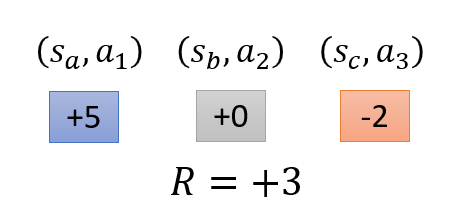
整个轨迹中的总收益是\(+3\)，但是在动作 \(a_2\) 之后的 \(S_c\) 和 \(a_3\) 是负向贡献，所以在状态 \((s_b,a_2)\) 后面的收益 \(0-2\) 才是真证的 \(a_2\) 的贡献(contribution)。所以可以将轨迹总收益替换为单个动作之后的部分收益

\[R_\tau\rightarrow\sum_{t'=t}^Tr_{t'} \]

但是现在还有一个问题，在计算 \(a_2\) 的贡献的时候是 \(+0-2\) 将后面 \(a_3\) 的奖励同权重求和，这也是不合理的，因为后面的所采取的动作也是随机的，或者说并不是完全由 \(a_2\) 所导致，所以需要在将后期的奖励乘上一个折扣因子(discount rate) 的 \(t-t'\) 次方

\[R_\tau\rightarrow\sum_{t'=t}^T\gamma^{t'-t} r_{t'},\quad \gamma<1 \]

这样就可以保证离 \(a_2\) 越近的动作所产生的奖励对 \(a_2\) 真实的贡献值占比越大 。

最后，我们定义一个Advantage function \(A_t\equiv\sum_{t'=t}^T\gamma^{t'-t} r_{t'}-b\), 收益的梯度就可以写成

\[\nabla \bar R_{\theta}\approx\frac{1}{N}\sum_{\tau=1}^N\sum_{t=1}^T A_t \nabla {\rm log}\pi_\theta(a_{\tau,t}|s_{\tau,t})\tag{4} \]

\(A_t(a_{\tau,t}|s_{\tau,t})\) 是 \(a_{\tau,t}\) 和 \(s_{\tau,t}\) 的函数，表示的是在当前状态 \(s_{\tau,t}\) 下， 动作\(a_{\tau,t}\) 相较于其他动作（平均收益为 \(b\) ）的优势。