[优选算法专题三二分查找——NO.19x 的平方根 ] - 实践

题目链接：

69. x 的平方根

题目描述

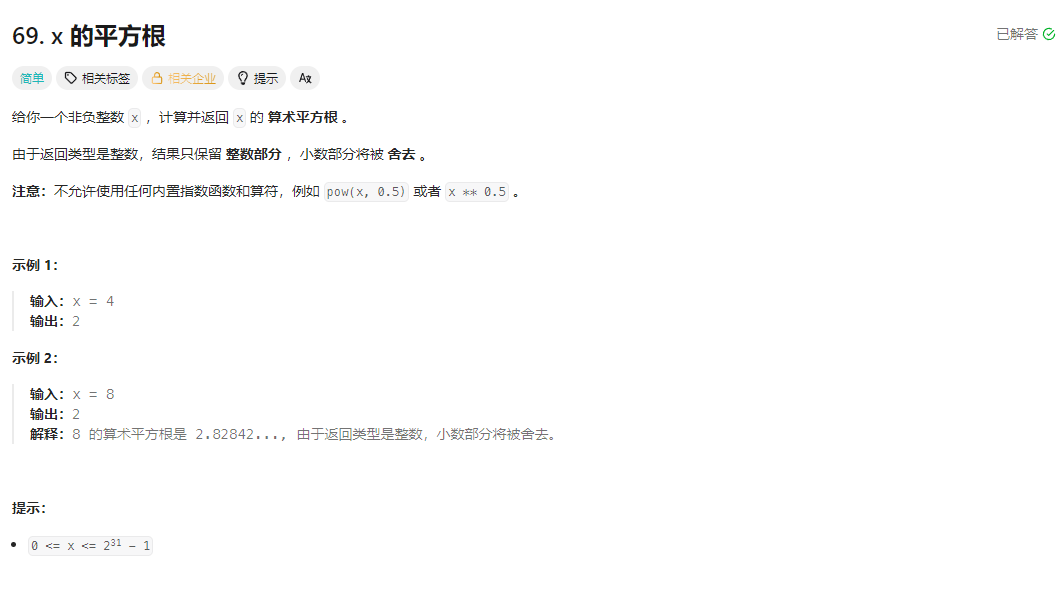
题目解答：

---

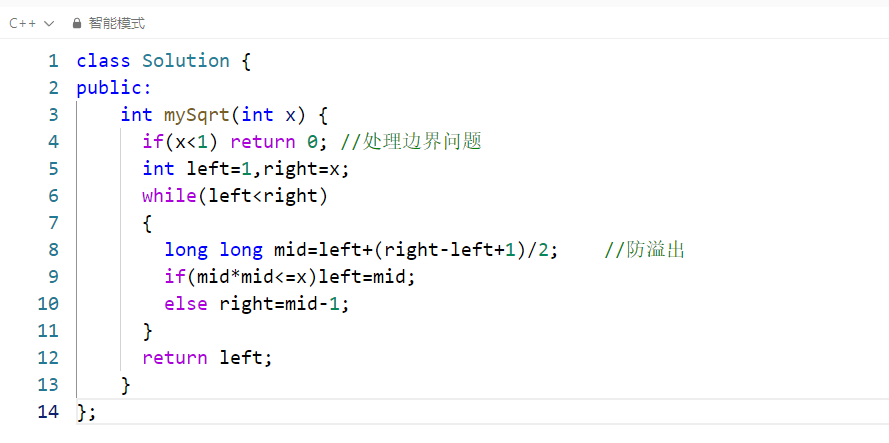
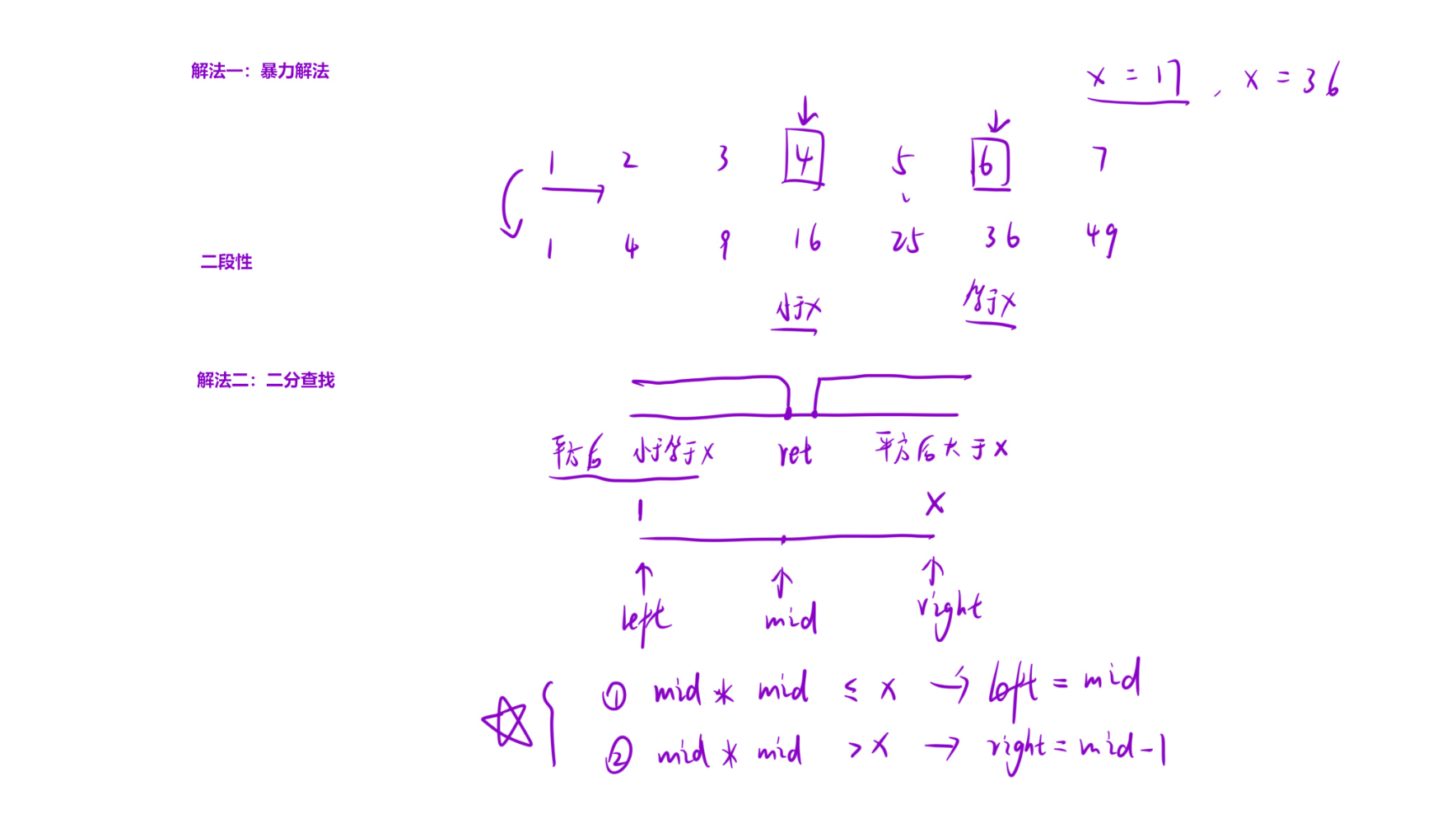
解析：

二、核心算法：二分查找（Binary Search）

代码采用 二分查找 而非暴力遍历，时间复杂度从 O(N) 优化到 O(log N)，是高效求解整数平方根的经典思路。

1. 二分查找的核心逻辑

二分查找的本质是通过不断缩小「可能的答案区间」，最终定位到唯一解。这里的「答案区间」是满足 k² ≤x 的所有整数 k 的范围。

步骤	代码逻辑	解释
1. 初始化区间	left=1, right=x	- 当 x≥1 时，其整数平方根一定在 [1, x] 之间（例如 x=1 时答案是 1，x=10 时答案在 1~10 之间）；- 边界情况 x<1（即 x=0）单独处理，直接返回 0。
2. 循环缩小区间	while(left < right)	当 left == right 时，区间内只剩一个数，即为答案。
3. 计算中间值	long long mid = left + (right - left + 1)/2	- 防溢出设计：若用 (left+right)/2，当 left 和 right 接近 INT_MAX（如 x=2¹⁶-1）时，left+right 会超出 int 范围，导致溢出；- +1 处理：避免「死循环」（下文单独解释）。
4. 判断并缩小区间	if(mid*mid ≤x) left=mid; else right=mid-1	- 若 mid² ≤x：说明 mid 是「可能的答案」，且更大的答案可能在 [mid, right] 中，因此将 left 移到 mid；- 若 mid² >x：说明 mid 太大，答案只能在 [left, mid-1] 中，因此将 right 移到 mid-1。

三、关键细节解析

1. 边界处理：if(x<1) return 0

• 题目中 x 是 非负整数（输入范围 0 ≤x ≤2³¹-1）；
• 当 x=0 时，其平方根是 0，直接返回避免后续二分查找的无效计算。

2. 防溢出设计：long long mid

• 若 mid 定义为 int，当 x 接近 2³¹-1（如 x=2³¹-1）时，mid 可能接近 1e5，mid*mid 会超出 int 的最大值（2³¹-1 ≈2.1e9），导致计算结果错误（例如 int 溢出后会变成负数，mid*mid ≤x 的判断会失效）；
• 用 long long 存储 mid，其范围是 -9e18 ~9e18，mid*mid 不会溢出，保证判断逻辑正确。

3. 避免死循环：mid = left + (right - left + 1)/2

这是二分查找中「向上取整」 的关键，若省略 +1，会出现死循环，例如：

• 假设 left=2，right=3，x=8（答案是 2）：
  • 若用 mid = (left+right)/2 = 2（向下取整）：
    • mid²=4 ≤8，执行 left=mid=2，此时 left 仍等于 2，right 仍等于 3，循环永远无法退出；
  • 若用 mid = left + (right-left+1)/2 = 2 + (1+1)/2 =3（向上取整）：
    • mid²=9 >8，执行 right=mid-1=2，此时 left=right=2，循环退出，返回正确答案。

四、代码执行示例（以 x=8 为例）

1. 初始：x=8 ≥1，left=1，right=8；
2. 第 1 次循环（left=1 < right=8）：
   • mid=1 + (8-1+1)/2 = 5；
   • mid²=25 >8 → right=5-1=4；
3. 第 2 次循环（left=1 < right=4）：
   • mid=1 + (4-1+1)/2 = 3；
   • mid²=9 >8 → right=3-1=2；
4. 第 3 次循环（left=1 < right=2）：
   • mid=1 + (2-1+1)/2 = 2；
   • mid²=4 ≤8 → left=2；
5. 循环结束（left=2 == right=2），返回 2（正确）。