LeetCode算法日记 - Day 61: 解数独、单词搜索(附带模版总结) - 指南
目录
1. 解数独
https://leetcode.cn/problems/sudoku-solver/
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例 1:

输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
1.1 题目解析
题目本质
约束满足问题(CSP)。在 9×9 棋盘上给每个空格分配 1~9,使其同时满足三类不重复约束:行、列、3×3 宫。
常规解法
最直观是回溯:遇到空格就从 1~9 试,能放则继续递归,失败就回退。
问题分析
朴素回溯在 k 个空格上存在最大 9^k 的分支,若不做状态记录,会重复尝试大量非法数,搜索树爆炸。预计在“已填较少、留白多”的局面耗时明显。
思路转折
要想高效 → 必须强剪枝 → 用三张状态表做 O(1) 合法性判断:
行:rowVis[9][10] 记录每行是否已用 1~9;
列:colVis[9][10] 记录每列是否已用 1~9;
宫:grid[3][3][10] 记录每个 3×3 宫是否已用 1~9。 预处理把已给定数字写入三表,搜索时只有“三表均未占用”的数字才尝试,回溯时对称撤销。这样可大幅缩小分支。
1.2 解法
算法思想:
三表剪枝:行/列/宫三维布尔表,O(1) 判断某数字是否能放到 (r,c)。
回溯搜索:找到下一个 '.' 空格,对 1..9 枚举;若三表均允许则放置→递归;失败则撤销继续试下一个。
终止条件:当整盘无 '.' 时,说明已填满且合法,返回 true 一路收敛。
i)初始化:扫描棋盘,对每个已填数字 d,设置 rowVis[r][d]=colVis[c][d]=grid[r/3][c/3][d]=true。
ii)搜索入口:调用 solve(),在棋盘上顺序寻找第一个 '.'。
iii)枚举尝试:对该空格从 1..9 枚举 d:若任一 rowVis/colVis/grid 已为真则跳过;否则落子并把三表置真,递归 solve()。
iv)回溯恢复:若递归失败,恢复该格为 '.',并把对应三表位置置回 false,继续尝试下一个数字。
v)结束返回:若 1..9 全部尝试无解,返回 false 让上层回溯;若棋盘已无空格,返回 true。
易错点:
字符与数字转换:放置用 (char)('0'+d),读取用 board[r][c]-'0'。
宫坐标:grid[r/3][c/3][d],注意整除分组正确。
回溯对称性:失败分支必须同时撤销棋盘字符与三表三处标记。
布尔表下标:使用 1..9,0 位置闲置,数组长度开到 10。
递归终止:当未再找到 '.' 时返回 true,勿继续搜索。
搜索顺序无关性:每层从 (0,0) 开始扫描找下一个空格即可,不需要记忆上一次位置
1.3 题目解析
class Solution {
boolean[][] rowVis, colVis;
boolean[][][] grid;
char[][] board;
public void solveSudoku(char[][] _board) {
rowVis = new boolean[9][10];
colVis = new boolean[9][10];
grid = new boolean[3][3][10];
board = _board;
// 预处理:把已填数字写入三张表
for (int r = 0; r < 9; r++) {
for (int c = 0; c < 9; c++) {
if (board[r][c] != '.') {
int d = board[r][c] - '0';
rowVis[r][d] = true;
colVis[c][d] = true;
grid[r/3][c/3][d] = true;
}
}
}
solve(); // 回溯求解(题目保证唯一解)
}
// 回溯:寻找下一个空格,尝试 1..9
private boolean solve() {
for (int r = 0; r < 9; r++) {
for (int c = 0; c < 9; c++) {
if (board[r][c] == '.') {
for (int d = 1; d <= 9; d++) {
if (rowVis[r][d] || colVis[c][d] || grid[r/3][c/3][d]) continue;
// 选择
board[r][c] = (char) ('0' + d);
rowVis[r][d] = colVis[c][d] = grid[r/3][c/3][d] = true;
if (solve()) return true; // 向后成功,直接收敛
// 撤销
board[r][c] = '.';
rowVis[r][d] = colVis[c][d] = grid[r/3][c/3][d] = false;
}
// 该空格 1..9 全失败,触发回溯
return false;
}
}
}
// 未找到空格,说明已填满
return true;
}
}复杂度分析
时间复杂度:最坏 O(9^k),k 为空格数;由于三表强剪枝,实际远小于最坏。
空间复杂度:O(k) 递归栈;三张表与棋盘大小常数级,O(1)。
2. 单词搜索
https://leetcode.cn/problems/word-search/
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
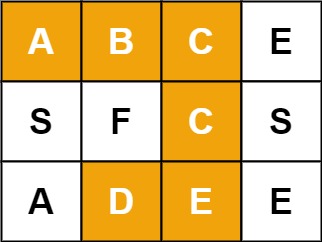
输入:board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "ABCCED"
输出:true示例 2:
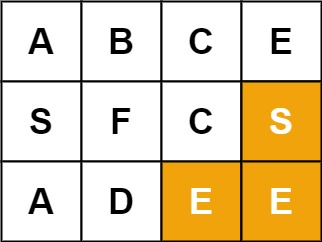
输入:board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "SEE"
输出:true示例 3:

输入:board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "ABCB"
输出:false提示:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15board和word仅由大小写英文字母组成
2.1 题目解析
题目本质
在二维网格中寻找一条路径,使得路径上依次经过的格子字符恰好组成给定字符串 word,且每个格子最多使用一次。属于典型的约束路径存在性问题(CSP + DFS 回溯)。
常规解法
从所有等于首字符的格子作为起点出发,进行深度优先搜索(DFS):每一层只匹配 word[pos],若相等则向四个相邻格子尝试匹配 word[pos+1],并用访问标记 vis 保证格子不被重复使用;若某条分支失败则回溯。
问题分析
朴素暴力如果不做访问标记或不回溯,会反复走回头路、形成错误环。
思路转折
要想写对写稳:
必须位置驱动:第 pos 层只匹配 word[pos](不要在同层对 word[pos..] 再做循环)。
必须成对回溯:进入格子前 vis[row][col]=true,所有子分支都失败后 vis[row][col]=false。
必须先判断终止:当 pos == word.length() 之前不可访问 word.charAt(pos);用“先判 pos==L 再取字符”的顺序消除越界风险。
2.2 解法
算法思想:
起点:遍历全盘,凡等于 word[0] 的格子都作为起点尝试。
递归:下一步要在四方邻居匹配 word[pos+1]”;当 pos == word.length() 说明整串已匹配完成。
访问控制:进入某邻居前置 vis[x][y]=true,回溯失败时恢复。起点在进入 DFS 前由外层设置与恢复。
若四个方向都失败,则撤销本格访问标记并返回 false。
i)读入网格尺寸,初始化 vis[m][n]。
ii)遍历每个格子 (i,j):若 board[i][j] == word[0],将其置为已访问并调用 isExist(i,j,1)。
iii)在 isExist 中:
若 pos == word.length(),返回 true(整串匹配完成)。
递归:取 ch = word.charAt(pos),在 4 个方向依次尝试:
邻格在界内、未访问、且字符等于 ch 时,先标记 vis[x][y]=true 再递归 pos+1;
若递归返回 true 立即向上返回 true;否则撤销标记继续试其它方向。
iv)若所有方向均失败,返回 false;外层起点也相应恢复访问标记并继续尝试下一个起点。
v)任一起点返回 true 即可终止整体搜索;全部失败则返回 false。
易错点:
终止判断位置:本实现采用“if (pos == word.length()) return true;”在读取 word.charAt(pos) 之前,避免越界。
不要在同一层对 word 再做 for(i=pos; …);这一层只匹配一个字符 word[pos],循环的是邻居。
起点标记与恢复:起点在外层枚举时标记与恢复,递归内不再重复标记起点自身。
回溯要对称:所有子分支失败后一定要把 vis[row][col] 恢复为 false。
2.3 代码实现
class Solution {
boolean[][] vis;
char[][] board;
String word;
int[] dx = {1,-1,0,0};
int[] dy = {0,0,1,-1};
int m,n;
StringBuffer path; // 保留你的风格,未使用
public boolean exist(char[][] _board, String _word) {
board = _board;
word = _word;
path = new StringBuffer();
m = board.length;
n = board[0].length;
vis = new boolean[m][n];
char ch = word.charAt(0);
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(board[i][j] == ch){
vis[i][j] = true; // 起点进入:先标记
boolean flag = isExist(i, j, 1); // pos=1,下一步去匹配 word[1]
if(flag) return true;
vis[i][j] = false; // 起点失败:恢复
}
}
}
return false;
}
// 从 (row,col) 开始,去邻居匹配 word[pos]
public boolean isExist(int row, int col, int pos){
if (pos == word.length()) return true; // 已匹配完整串
char ch = word.charAt(pos);
for(int k = 0; k < 4; k++){
int x = row + dx[k], y = col + dy[k];
if(x>=0 && x=0 && y
复杂度分析:
时间复杂度:最坏 O(mn * 4^L),L = word.length。每个起点触发一棵深度 L、分支因子≤4 的搜索树。
空间复杂度:O(L) 递归栈,外加 O(mn) 的 vis 布尔表(一次分配、反复复用)
3. 模版总结
场景一:位置驱动、按顺序遍历(顺序固定,位置推进)
特点:元素的相对顺序不改变,递归深度=位置/下标(pos/idx)。这一层不在“剩余元素里任选”,而是在当前顺序位置上决定“怎么扩展到下一位置”。
常见题:
组合/子集:从 start 往后挑,不改变原顺序;
- Word Search:pos 固定匹配 word[pos],向邻居扩展到 pos+1;
模版例如:
void dfs(int start) {
collect(path); // 每层都是合法前缀,可收集
for (int i = start; i < n; i++) {
if (i > start && nums[i] == nums[i-1]) continue; // 同层去重(可选)
path.add(nums[i]);
dfs(i + 1); // 顺序推进
path.remove(path.size()-1); // 回溯
}
}
识别信号:
“保序、不换位”,或“按下标/位置一步步推进(pos→pos+1)”;
本层循环多发生在动作集合(邻居/后续索引)上,而不是在“剩余元素”上任取。
场景二:选择驱动、不按顺序遍历(顺序可变,候选池里任选下一个)
特点:可以改变元素顺序;本层循环对象是候选池,常用 used[] 控制是否已选。 常见题:
全排列、带约束的排列(安排顺序/排座位/行程安排)。
模版例如:
void dfs() {
if (path.size() == n) { collect(path); return; }
for (int i = 0; i < n; i++) {
if (used[i]) continue;
used[i] = true;
path.add(nums[i]);
dfs();
path.remove(path.size()-1);
used[i] = false;
}
}
识别信号:
目标是“所有不同顺序/排列”;
需要从未使用的元素中任选一个作为下一位。
有重复元素时:排序 + “同层去重”条件:
if (i>0 && nums[i]==nums[i-1] && !used[i-1]) continue;
场景三:二叉遍历(选 or 不选)
特点:对第 idx 个元素做二选一;整棵树是二叉的,叶子对应一个完整选择方案。
常见题:
子集、01 决策类
模版例如:
void dfs(int idx) {
if (idx == n) { collect(path); return; }
// 1) 选 idx
path.add(nums[idx]);
dfs(idx + 1);
path.remove(path.size()-1);
// 2) 不选 idx
dfs(idx + 1);
}
识别信号:
每个位置只有“要 / 不要”两种决策;
不需要在同层遍历不同候选,只对当前下标做决定。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号