深入浅出朴素贝叶斯算法：原理、实现与应用 - 指南

朴素贝叶斯（Naive Bayes）是一种基于贝叶斯定理和特征条件独立性假设的分类算法。尽管它看似简单，却在文本分类、垃圾邮件过滤、情感分析等领域表现出色。本文将深入解析朴素贝叶斯的数学原理，介绍 Python 实现途径，并凭借实例代码展示其应用。

朴素贝叶斯的数学原理

贝叶斯定理

朴素贝叶斯算法的核心是贝叶斯定理，其数学表达式如下：

P(A|B) = P(B|A) *P(A)/P(B)

其中：

• P(A|B) 是后验概率：在 B 发生的情况下 A 发生的概率
• (P(B|A) 是似然度：在 A 发生的情况下 B 发生的概率
• (P(A) 是先验概率：A 发生的概率
• (P(B) 是边际概率：B 发生的概率

在分类挑战中，我们将 A 视为 "类别"，B 视为 "特征"，则公式变为：

P(类别|特征) = P(特征|类别)*P(类别)/P(特征)

朴素假设：

朴素贝叶斯的 "朴素" 之处在于它假设所有特征之间是条件独立的。这一假设大大简化了计算，使大家可以将联合概率分解为多个边缘概率的乘积：

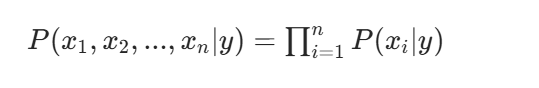
其中 x1, x2, ..., xn 是特征，y 是类别。

分类决策：

对于给定样本，大家计算其属于每个类别的后验概率，然后选择概率最大的类别作为预测结果：

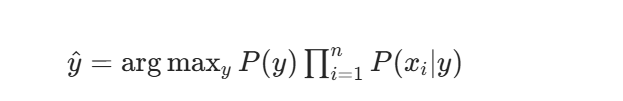
由于 P(特征)对于所有类别都是相同的，在比较时允许忽略。

计算示例

让我们凭借一个简单的例子理解朴素贝叶斯的计算过程。假设我们有以下关于天气与是否打球的资料：

序号	天气	温度	湿度	风速	是否打球
1	晴朗	炎热	高	弱	否
2	晴朗	炎热	高	强	否
3	多云	炎热	高	弱	是
4	下雨	适中	高	弱	是
5	下雨	凉爽	正常	弱	是
6	下雨	凉爽	正常	强	否
7	多云	凉爽	正常	强	是
8	晴朗	适中	高	弱	否
9	晴朗	凉爽	正常	弱	是
10	下雨	适中	正常	弱	是

现在要求预测：当天气为 "晴朗"，温度为 "凉爽"，湿度为 "正常"，风速为 "强" 时，是否适合打球？

步骤 1：计算先验概率

• P(是) = 6/10 = 0.6
• P(否) = 4/10 = 0.4

步骤 2：计算似然度对于 "是" 的情况：

• P(晴朗|是) = 2/6 ≈ 0.333
• ) = 3/6 = 0.5就是P(凉爽|
• P(正常|是) = 4/6 ≈ 0.667
• ) = 2/6 ≈ 0.333就是P(强|

对于 "否" 的情况：

• P(晴朗|否) = 3/4 = 0.75
• P(凉爽|否) = 1/4 = 0.25
• P(正常|否) = 1/4 = 0.25
• P(强|否) = 2/4 = 0.5

步骤 3：计算后验概率

• (P(是|特征) ∝ P(是) * P(晴朗|是) * P(凉爽|是) * P(正常|是) * P(强|是) ≈ 0.6 * 0.333 * 0.5* 0.667 *0.333 ≈ 0.022
• (P(否|特征) ∝ P(否) * P(晴朗|否) *P(凉爽|否) *P(正常|否) * P(强|否) ≈ 0.4 * 0.75 * 0.25* 0.25 *0.5 ≈ 0.0094

结论：因为 0.022 > 0.0094，因此预测结果为 "是"，适合打球。

Python 实现朴素贝叶斯的方法与库

实现朴素贝叶斯分类器许可使用现有库，利用成熟的机器学习库，适合实际应用

常用的 Python 库包括：

• scikit-learn：提供了多种朴素贝叶斯实现（GaussianNB, MultinomialNB, BernoulliNB 等）
• numpy：用于数值计算
• pandas：用于数据处理
• nltk/scikit-learn：用于文本特征提取（对文本分类特有有用）

实例代码：使用朴素贝叶斯进行鸢尾花分类

下面我们将使用 scikit-learn 库实现朴素贝叶斯分类器，并应用于经典的鸢尾花数据集。

示例代码：

# 朴素贝叶斯分类器实例：鸢尾花分类
# 导入必要的库
import numpy as np  # 导入numpy库，用于数值计算
import pandas as pd  # 导入pandas库，用于数据处理和分析
from sklearn.datasets import load_iris  # 从sklearn数据集模块导入鸢尾花数据集
from sklearn.model_selection import train_test_split  # 导入数据集拆分工具
from sklearn.naive_bayes import GaussianNB  # 导入高斯朴素贝叶斯分类器
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix  # 导入模型评估指标
# 加载鸢尾花数据集
iris = load_iris()  # 将鸢尾花数据集加载到变量iris中
# 查看数据集信息
print("数据集特征名称:", iris.feature_names)  # 打印特征名称（花萼长度、宽度等）
print("数据集类别:", iris.target_names)  # 打印鸢尾花的三个类别名称
print("数据集形状:", iris.data.shape)  # 打印数据集形状（样本数×特征数）
# 将数据转换为DataFrame以便更好地查看
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)  # 创建DataFrame，使用特征数据和特征名称
df['species'] = pd.Categorical.from_codes(iris.target, iris.target_names)  # 添加物种列，将数字标签转换为实际物种名称
print("\n数据集前5行:")
print(df.head())  # 打印数据集的前5行，查看数据格式
# 划分训练集和测试集
X = iris.data  # 特征数据，即花的测量数据
y = iris.target  # 标签数据，即花的类别（0、1、2分别代表三个品种）
# 随机划分80%作为训练集，20%作为测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42  # test_size=0.2表示测试集占20%，random_state确保结果可重现
)
# 创建并训练朴素贝叶斯分类器
# 对于连续特征，我们使用高斯朴素贝叶斯
gnb = GaussianNB()  # 实例化高斯朴素贝叶斯分类器
gnb.fit(X_train, y_train)  # 使用训练数据拟合模型，即训练分类器
# 预测
y_pred = gnb.predict(X_test)  # 使用训练好的模型对测试集进行预测，得到预测标签
# 评估模型性能
print("\n模型评估:")
print(f"准确率: {accuracy_score(y_test, y_pred):.4f}")  # 计算并打印准确率（正确预测的比例）
print("\n混淆矩阵:")
print(confusion_matrix(y_test, y_pred))  # 打印混淆矩阵，展示各类别预测情况
print("\n分类报告:")
# 打印分类报告，包含精确率、召回率、F1分数等详细指标
print(classification_report(y_test, y_pred, target_names=iris.target_names))
# 查看预测概率
print("\n前5个测试样本的预测概率:")
# 打印前5个测试样本属于每个类别的概率
print(gnb.predict_proba(X_test[:5]))
# 使用训练好的模型进行新样本预测
# 假设我们有一个新的鸢尾花样本，其特征如下
new_sample = [[5.1, 3.5, 1.4, 0.2]]  # 新样本的特征数据（花萼长度、花萼宽度、花瓣长度、花瓣宽度）
prediction = gnb.predict(new_sample)  # 预测新样本的类别
prediction_proba = gnb.predict_proba(new_sample)  # 获取新样本属于每个类别的概率
print("\n新样本预测结果:")
print(f"预测类别: {iris.target_names[prediction][0]}")  # 打印预测的类别名称
print(f"预测概率: {prediction_proba[0]}")  # 打印属于每个类别的概率