三维旋转：旋转矩阵，欧拉角，四元数

原文见我的博客主站，欢迎大家过去评论。

如何描述三维空间中刚体的旋转，是个有趣的问题。具体地说，就是刚体上的任意一个点P(x, y, z)围绕过原点的轴(i, j, k)旋转θ，求旋转后的点P\'(x\', y\', z\')。

旋转矩阵

旋转矩阵乘以点P的齐次坐标，得到旋转后的点P'，因此旋转矩阵可以描述旋转，

$$\begin{bmatrix}x'\\ y'\\ z'\\ 1\end{bmatrix}=R\cdot \begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$

绕x，y，或z轴旋转θ的矩阵为：

$$R_{x}(\theta)=\begin{bmatrix}1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta\end{bmatrix}$$

$$R_{y}(\theta)=\begin{bmatrix}\cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0\\ \sin\theta & 0 & \cos\theta\end{bmatrix}$$

$$R_{z}(\theta)=\begin{bmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1\end{bmatrix}$$

所以，绕任意轴旋转的矩阵为

$$R_{x}(-p)\cdot R_{y}(-q)\cdot R_{z}(\theta)\cdot R_{y}(q)\cdot R_{x}(p)$$

这表示：

1. 绕x轴旋转角度p使指定的旋转轴在xz平面上
2. 绕y轴旋转角度q使指定的旋转轴与z轴重合
3. 绕z轴旋转角度θ
4. 绕y轴旋转角度-q
5. 绕x轴旋转角度-p

其中，p和q的值需要用i,j,k计算出来。

欧拉角

欧拉角也可以描述三维刚体旋转，它将刚体绕过原点的轴(i,j,k)旋转θ，分解成三步（蓝色是起始坐标系，而红色的是旋转之后的坐标系。）。

 

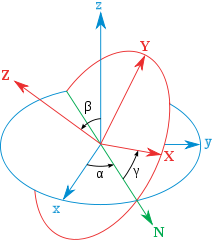
1. 绕z轴旋转α，使x轴与N轴重合，N轴是旋转前后两个坐标系x-y平面的交线
2. 绕x轴（也就是N轴）旋转β，使z轴与旋转后的z轴重合
3. 绕z轴旋转γ，使坐标系与旋转后的完全重合

按照旋转轴的顺序，该组欧拉角被称为是“zxz顺规”的。对于顺规的次序，学术界没有明确的约定。

欧拉角的旋转矩阵为：

$$R_{z}(α)\cdot R_{x}(β)\cdot R_{z}(γ)$$

在旋转矩阵一节中，最先进行的旋转其矩阵在最右侧，说明该矩阵最先与点的齐次坐标相乘，旋转矩阵按照旋转的次序从右向左排列。而在欧拉角中，最先进行的旋转其旋转矩阵在最左边。这是因为，**对于前者（旋转矩阵），我们始终是以绝对参考系为参照来的，对于后者（欧拉角），我们每一次旋转的刻画都是基于刚体的坐标系。**比如，在欧拉角中的第2步，绕x轴旋转β，这里的x轴实际上是N轴了（而不是蓝色的x轴）。

为什么旋转参考系的不同会导致旋转矩阵次序的差异呢？细想一下便知，旋转矩阵左乘叠加用以描述三维变换效果的叠加，这本身就是基于绝对坐标系的，所以旋转矩阵一节没有疑问；而对于欧拉角一节的这种旋转方式，这样考虑：

1. 如果有一个“影子坐标系3”与原坐标系重合，然后首先进行了第3步（绕z轴旋转γ）；
2. 然后有一个“影子坐标系2”也与原坐标系重合，然后与“影子坐标系3”一起（视作同一个刚体）进行了第二步；
3. 最后一个“影子坐标系1”，与前两个坐标系一起进行了第一步。

此时，考察“影子坐标系”1和2，他们就分别落在了欧拉角旋转的两个“快照”上，而“影子坐标系3”就落在旋转后的位置上（红色的）。而在上述过程中，“影子坐标系3”就是相对于绝对坐标系依次进行了第三步，第二步，和第一步。所以欧拉角的旋转矩阵写成那样，也是行得通的。

这个想法，我猜在很多第一人称游戏中，已经得到了广泛应用了。这样，玩家对人物的控制就可以绕开人物的实时状态（位置，角度等）直接对人物的模型矩阵产生影响。

万向节死锁是欧拉角的一个弊端，这是一个直观的例子。

四元数

四元数是今天的主角，它能够很方便的刻画刚体绕任意轴的旋转。四元数是一种高阶复数，四元数q表示为：

$$q=(x,y,z,w)=xi+yj+zk+w$$

其中，i，j，k满足：

$$i^2=j^2=k^2=-1$$

$$ij=k,jk=i,ki=j$$

由于i，j，k的性质和笛卡尔坐标系三个轴叉乘的性质很像，所以可以将四元数写成一个向量和一个实数组合的形式：

$$q=(\vec{v}+w)=((x,y,z),w)$$

可以推导出四元数的一些运算性质，包括：

* 四元数乘法

$$q1q2=(\vec{v_1}\times \vec{v_2}+w_1\vec{v_2}+w_2\vec{v_1}, w_1w_2-\vec{v_1}\cdot \vec{v_2})$$

* 共轭四元数

$$q^*=(-\vec{v},w)$$

* 四元数的平方模

$$N(q)=N(\vec{v})+w^2$$

* 四元数的逆

$$q^{-1}=\frac{q^*}{N(q)}$$

四元数可以看做是向量和实数的一种更加一般的形式，向量可以视作为实部为0的四元数，而实数可以是作为虚部为0的四元数。上述四元数的运算性质也是实数或向量的运算性质的更一般的形式。

四元数可用来刻画三维空间中的旋转，绕单位向量(x,y,z)表示的轴旋转θ，可令：

$$q=((x,y,z)\sin{\frac{\theta}{2}},\cos{\frac{\theta}{2}})$$

刚体坐标系中的点p(P,0)（写成四元数的形式），旋转后的坐标p'为：

$$p'=qpq^{-1}$$

接下来我们来证明这一点。

首先，我们证明

$qpq^{-1}=(sq)p(sq)^{-1}$

其中s为实数。显然

$$(sq)p(sq)^{-1}=sqpq^{-1}s^{-1}=sqp^{-1}$$

此时，我们可以将q看做是单位矩阵，因为如果q不是单位矩阵，我们就可以乘以一个常数s将其化为单位矩阵。

然后，我们证明qpq^{-1}和p的模长相等

下面将q视为单位四元数：

$$q^{-1}=q^*$$

四元数q的标量:

$$S(q)=(q+q^*)/2$$

那么：

$$2S(qpq^{-1})=2S(qpq^*)=qpq^*+(qpq^*)^*=qpq^*+qp^*q^*=q(p+p^*)q^*=q2S(p)q^*=2S(p)$$

最后，我们证明

$$p'=qpq^*$$

如图所示，u为旋转轴，旋转角度为σ，向量v旋转到w处。旋转到σ/2处为k（图中未标出）。

下面也用相同的字母指代四元数，如u就表示向量u的四元数形式((ux,uy,uz),0)。

首先，令u方向上的单位向量为u（为了方便，命名不变，后面的u都是指旋转轴方向的单位四元数），那么根据q的定义，参见四元数乘法法则：

$$q=(\vec{u}\sin{\frac{\theta}{2}},\cos{\frac{\theta}{2}})=(\vec{v}\times\vec{k},\vec{v}\cdot \vec{k})=(\vec{v},0)(-\vec{k},0)=kv^*$$

现在令

$$w=qvq^*$$

如果能证明w与v的夹角是σ，那么就说明w确实是v旋转σ得到的，整个命题就得证了。

注意v，k和w都是实部为0的单位四元数，表示单位向量，我们有：

$$wk^*=(qvq^{-1})k^*=qvq^*k^*=qvvk^*k^*=q$$

所以

$$wk^*=kv^*$$

上面的式子拆分成实部和虚部，虚部表明w与-k的平面和k与-v的平面重合，实部表明w和-k之间的夹角与k和-v之间的夹角相等，都是π-σ/2。这就说明了w与v的夹角是σ，原命题就得证了。