搜索(Search)
一.深度优先搜索(DFS)Deep Firts Search
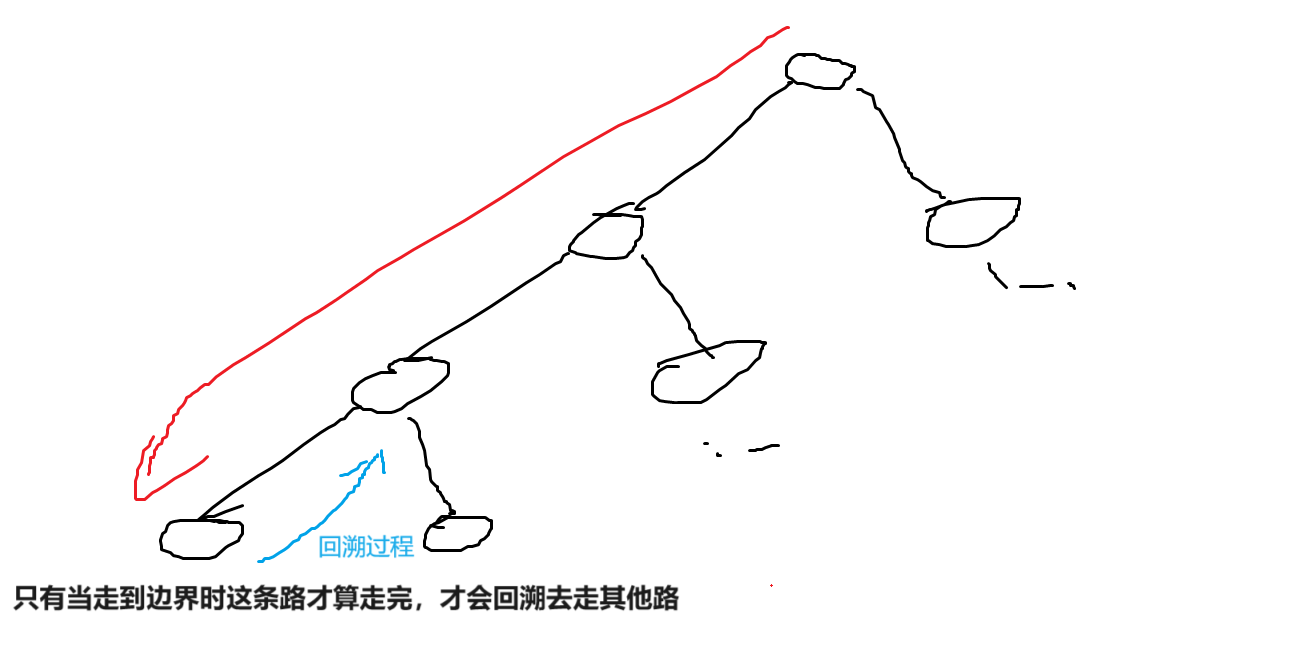
简单来说就是一句话:"不撞南墙不回头"。
如下图:
代码模板:
void dfs(int k){K代表递归层数,或者说要填第几个空
if(所有空已经填完了){
判断最优解 / 记录答案;
return;
}
for(枚举这个空能填的选项){
if(这个选项是合法的){
记录下这个空 (保存现场)
dfs(k+1);
取消这个空 (恢复现场) (就是回溯过程,dfs很重要)
}
}
}
例题:四阶数独
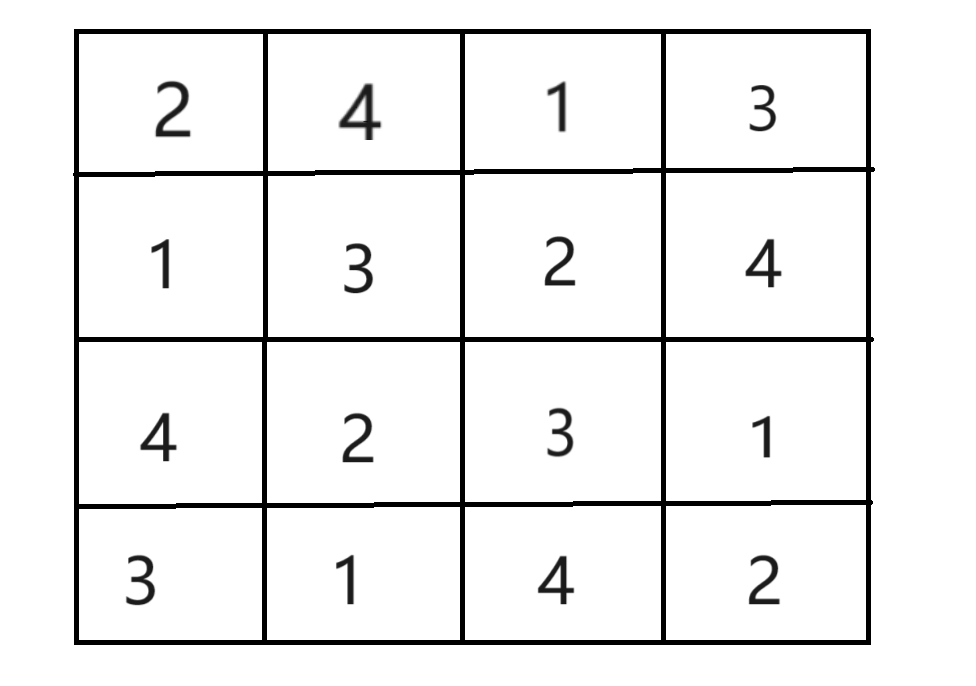
给出一个 4 * 4 的格子,每个格子只能填写 1 到 4 的整数,要求每一行,每一列和四等分更小的正方形的部分都刚好由 1 到 4 组成。下图所示是一个合法的四阶数独的例子。
给出空白的方格,请问:一共有多少种合法的填方案?
分析:
既然每一行都是 1 到 4,假设各行都是独立的,分别枚举 1 到 4 的全排列,组成一个 4 * 4 的矩阵,然后判断这个矩阵是否符合数独的要求。重要的是,在枚举的时候,一旦发现某位数字不符合要求,立刻中断这种情况的枚举,能省time。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int ans=0,n=16,a[25];
int b1[5][5],b2[5][5],b3[5][5];// 分别记录横行,竖行,四小块
void dfs(int x)
{
if(x>n){
ans++;
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
if(i%4==0)cout<<endl;
}
cout<<endl;
return;
}
int row=(x-1)/4+1;// 横排编号
int col=(x-1)%4+1;// 竖排编号
int block=(row-1)/2*2+(col-1)/2+1;// 小块编号
for(int i=1;i<=4;i++){
if(b1[row][i]==0&&b2[col][i]==0&&b3[block][i]==0){
a[x]=i;// 记录放置位置
b1[row][i]=1; b2[col][i]=1; b3[block][i]=1;// 占位
dfs(x+1);// 下一层递归
b1[row][i]=0; b2[col][i]=0; b3[block][i]=0;// 取消占位
}
}
}
int main()
{
dfs(1);
cout<<ans<<endl;
}
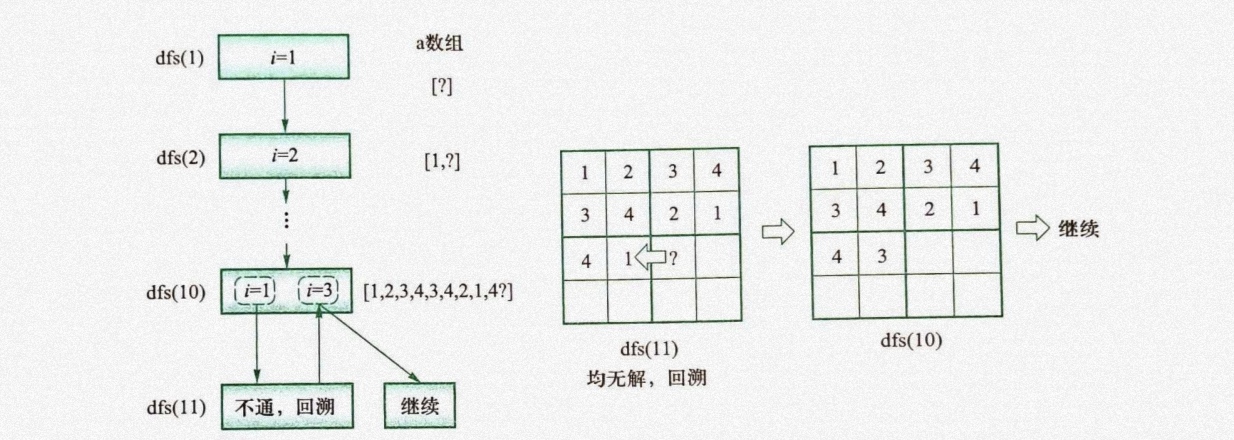
模拟代码过程:

例题:
题目链接:https://www.luogu.com.cn/problem/P1219
题解:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100;
int ans=0,a[maxn],b1[maxn],b2[maxn],b3[maxn],n;
void dfs(int x){
if(x>n){
ans++;
if(ans<=3){
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
}
return;
}
for(int i=1;i<=n;i++){
if(b1[i]==0&&b2[x+i]==0&&b3[x-i+15]==0){// +15 是防止下标为负数
a[x]=i;
b1[i]=1,b2[x+i]=1,b3[x-i+15]=1;
dfs(x+1);
b1[i]=0,b2[x+i]=0,b3[x-i+15]=0;
}
}
}
int main()
{
cin>>n;
dfs(1);
cout<<ans<<endl;
}
二.广度优先搜索(BFS) Breadth First Search
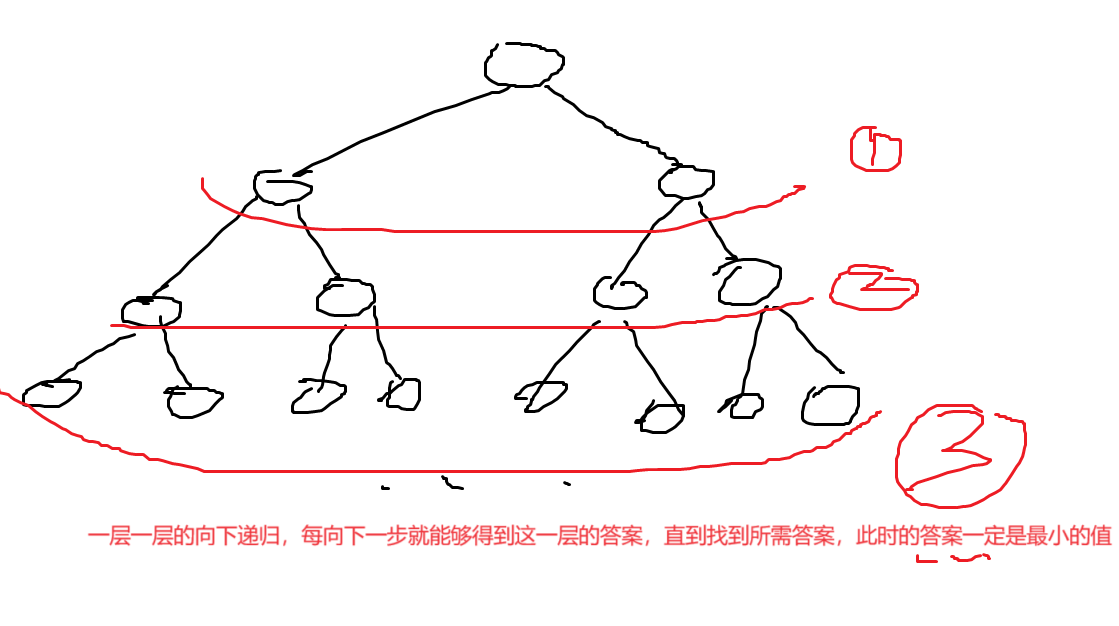
以层为单位往下递归,比DFS快。多用于求最短路径等问题。
例题:
P1443 马的遍历
题解1:(用队列来写)
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N = 410;
typedef pair<int, int> PII;
int n, m, x1, y2;
int dist[N][N]; //存地图
int dx[] = {2, 2, 1, 1, -1, -1, -2, -2};
int dy[] = {-1, 1, -2, 2, -2, 2, -1, 1};
queue<PII> q;
void bfs(int x1, int y1) {
memset(dist, -1, sizeof dist);
q.push({x1,y1}); //进队
dist[x1][y1] = 0; //起点标记
while(!q.empty()) {
auto t = q.front(); //取出对头
q.pop(); //弹出对头
for(int i = 0; i < 8; i ++) {
int a = t.x + dx[i], b = t.y + dy[i];
// 判断所有不合理的条件
if(a < 1 || a > n || b < 1 || b > m) continue;
if(dist[a][b] >= 0) continue;
q.push({a, b});//下一个点入队
dist[a][b] = dist[t.x][t.y] + 1;// 满足则答案++;
}
}
}
int main() {
scanf("%d %d %d %d", &n, &m, &x1, &y2);
bfs(x1, y2);
for(int i = 1; i <= n; i ++) {
for(int j = 1; j <= m; j ++) {
printf("%-5d", dist[i][j]);
}
printf("\n");
}
return 0;
}
题解2:(用数组模拟队列,这会比用队列快,注重理解)
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N = 410;
typedef pair<int, int> PII;
int n, m, x1, y2;
int dist[N][N]; //存地图
int dx[] = {2, 2, 1, 1, -1, -1, -2, -2};
int dy[] = {-1, 1, -2, 2, -2, 2, -1, 1};
PII q[N * N];
void bfs(int x1, int y1) {
memset(dist, -1, sizeof dist);
q[0] = {x1, y1}; //进队
dist[x1][y1] = 0; //起点标记
int hh = 0, tt = 0;
while(hh <= tt) {
auto t = q[hh ++]; //取出对头
for(int i = 0; i < 8; i ++) {
int a = t.x + dx[i], b = t.y + dy[i];
if(a < 1 || a > n || b < 1 || b > m) continue;
if(dist[a][b] >= 0) continue;
dist[a][b] = dist[t.x][t.y] + 1;
q[++tt] = {a, b};
}
}
}
int main() {
scanf("%d %d %d %d", &n, &m, &x1, &y2);
bfs(x1, y2);
for(int i = 1; i <= n; i ++) {
for(int j = 1; j <= m; j ++) {
printf("%-5d", dist[i][j]);
}
printf("\n");
}
return 0;
}
以上只是对搜索有个简单的认识,要想 理解的深刻,还得多做题,加油!!!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号