leetcode 62. 不同路径-java实现

题目所属分类

简单DP 从左上到右下

原题链接

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

代码案例：

题解

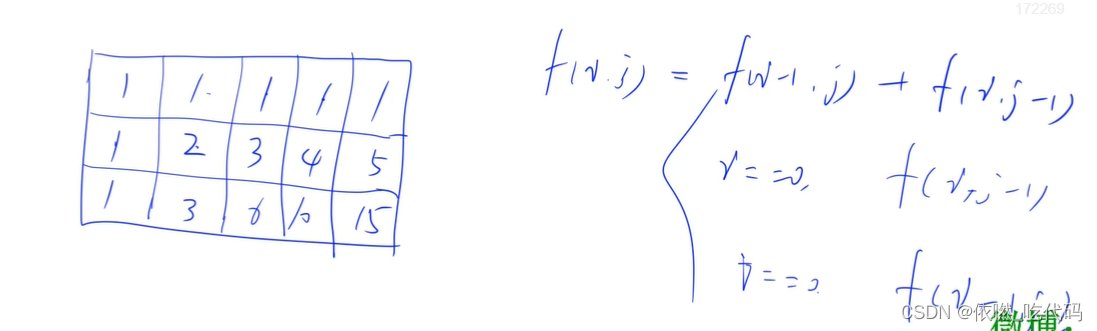
写法有好几种 达到最终目的即可
第一种方法推荐

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] f = new int[m][n];
        for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ; j++){
                if(i==0 && j ==0 ) f[i][j]  =1 ;
                else{
                //可以从上面走
                    if(i != 0) f[i][j] += f[i-1][j];
                 //可以从左边走
                    if(j != 0) f[i][j] += f[i][j-1];
                }
            }
        }
        return f[m-1][n-1];
    }
}

图片中的原始方法

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] f = new int[m][n];
        for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ; j++){
                if(i==0 && j ==0 ) f[i][j]  =1 ;
                else{
                    if(i == 0) f[i][j] = f[i][j-1];

                 else   if(j == 0) f[i][j] = f[i-1][j];

                 else    f[i][j] = f[i-1][j] + f[i][j-1];
                }
            }
        }
        return f[m-1][n-1];
    }
}

从i=1开始算的话

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i++) dp[i][0] = 1;
        for(int i = 1; i < n; i++) dp[0][i] = 1;
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}