【实验4】函数和数组

 

 

 

 

 

实验任务一

 

 

原始程序代码：

// 一元二次方程求解
// 重复执行， 直到按Ctrl+Z结束
//
#include <math.h>
#include <stdio.h>
int main() {
    float a, b, c, x1, x2;
    float delta, real, imag;
    printf("Enter a, b, c: ");
    while(scanf("%f%f%f", &a, &b, &c) != EOF) {
        if(a == 0)
        printf("not quadratic equation.\n\n");
        else {
            delta = b*b - 4*a*c;
            if(delta >= 0) {
            x1 = (-b + sqrt(delta)) / (2*a);
            x2 = (-b - sqrt(delta)) / (2*a);
            printf("x1 = %.2f, x2 = %.2f\n\n", x1, x2);
            }
            else {
            real = -b/(2*a);
            imag = sqrt(-delta) / (2*a);
            printf("x1 = %.2f + %.2fi, x2 = %.2f - %.2fi\n\n", real,
            imag, real, imag);
            }
        }
        printf("Enter a, b, c: ");
    }
return 0;
}

 

 

改版程序代码：

// 一元二次方程求解（函数实现方式）
// 重复执行， 直到按下Ctrl+Z结束
#include <math.h>
#include <stdio.h>
// 函数声明
void solve(double a, double b, double c);
// 主函数
int main() {
    double a, b, c;
    printf("Enter a, b, c: ");
    while(scanf("%lf%lf%lf", &a, &b, &c) != EOF) {
        solve(a, b, c); // 函数调用
        printf("Enter a, b, c: ");
    }
    return 0;
}
// 函数定义
// 功能：求解一元二次方程，打印输出结果
// 形式参数：a,b,c为一元二次方程系数
void solve(double a, double b, double c) {
    double x1, x2;
    double delta, real, imag;
    if(a == 0)
        printf("not quadratic equation.\n");
    else {
        delta = b*b - 4*a*c;
        if(delta >= 0) {
            x1 = (-b + sqrt(delta)) / (2*a);
            x2 = (-b - sqrt(delta)) / (2*a);
            printf("x1 = %f, x2 = %f\n", x1, x2);
        }
        else {
            real = -b/(2*a);
            imag = sqrt(-delta) / (2*a);
            printf("x1 = %f + %fi, x2 = %f - %fi\n", real, imag, real,imag);
        }
    }
}

解析：

1、定义函数solve，则在这个计算一元二次方程的程序中的共能肯定是进行公式求解。

2、既然是用公式求解来定义函数，那么输入的形参肯定就是三个，“a,b,c"。

3、通过公式计算出结果可以作为函数返回值也可以直接打印，二者都同等方便，仅看使用者需求。

4、若是无返回值的方式编写solve函数，则其应当具有判断是否能成功调用程序至输出结果、计算实参、以及打印计算结果。

　  若是带返回值的方式，则应当将计算的两根的结果返回给main函数。

5、对比前后两版本的程序，修改的地方无非是让主函数的功能由输入、计算、输出变化为输入、引用函数，而已。

　  使主函数看起来更加的简洁明了，意图容易理解。

 

 

 

---

 

 

 

 

 

实验任务二

 

原始程序：

// 利用局部static变量计算阶乘
#include <stdio.h>
long long fac(int n); // 函数声明
int main() {
    int i,n;
    printf("Enter n: ");
    scanf("%d", &n);
    for(i=1; i<=n; ++i)
        printf("%d! = %lld\n", i, fac(i));
    return 0;
}
// 函数定义
long long fac(int n) {
    static long long p = 1;
    p = p*n;
    return p;
}

运行结果：

 

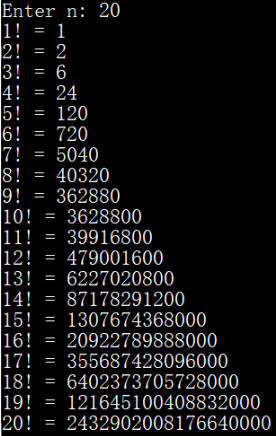
为了探究局部static变量

增加一行代码： printf("p = %lld\n", p); 

修改程序：

// 利用局部static变量计算阶乘
#include <stdio.h>
long long fac(int n); // 函数声明
int main() {
    int i,n;
    printf("Enter n: ");
    scanf("%d", &n);
    for(i=1; i<=n; ++i)
        printf("%d! = %lld\n", i, fac(i));
    return 0;
}
// 函数定义
long long fac(int n) {
    static long long p = 1;
    printf("p = %lld\n", p);
    p = p*n;
    return p;
}

运行结果：

 

明显可见，虽然在fac（）函数的首段具有p的初始化，但是p的值一直保留着上一次调用结果的p值。

 

例题：

// 练习：局部static变量特性
#include<stdio.h>
int func(int, int);
int main() {
    int k=4,m=1,p1,p2;
    p1 = func(k,m) ;
    p2 = func(k,m) ;
    printf("%d,%d\n",p1,p2) ;
    return 0;
}
int func(int a,int b) {
    static int m=0,i=2;
    i += m+1;
    m = i+a+b;
    return (m);
}

猜想打印结果：8 17

 

 

 

 

 

 

---

 

 

 

实验任务三

 

 

 

题目：填入空缺代码

//寻找两个整数之间的所有素数(包括这两个整数),把结果保存在数组bb中,函数返回素数的个数。
// 例如，输入6和21,则输出为:7 11 13 17 19。
#include <stdio.h>
#define N 1000
int fun(int n,int m,int bb[N]) {
    int i,j,k=0,flag;
    for(j=n;j<=m;j++) {
        flag=1;/*补足1*/
        for(i=2;i<j;i++)
            if(j%i==0/*补足2*/) {
                flag=0;
                break;
            }
        if(flag!=0/*补足3*/)
            bb[k++]=j;
    }
    return k;
}
int main(){
    int n=0,m=0,i,k,bb[N];
    scanf("%d",&n);
    scanf("%d",&m);
    for(i=0;i<m-n;i++)
        bb[i]=0;
    k=fun(n,m,bb/*补足4*/);
    for(i=0;i<k;i++)
        printf("%4d",bb[i]);
    return 0;
}

 

运行结果：

 

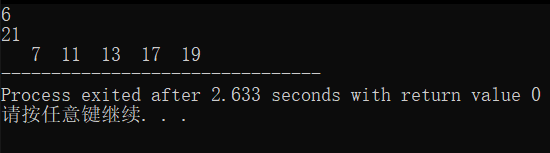
思路：

补足1：将flag初始化，作为判定是否为素数的标志

补足2：测试目前检查的这个整数是否能被一个数整除

补足3：如果已经判断出该数为素数

补足4：以主函数中的变量调用函数

 

 

 

---

 

 

 

 

 

实验任务四

例题：实现f(n)=2^n-1

程序：

#include <stdio.h>
long long fun(int n); // 函数声明
int main() {
    int n;
    long long f;
    while(scanf("%d", &n) != EOF) {
        f = fun(n); // 函数调用
        printf("n = %d, f = %lld\n", n, f);
    }
    return 0;
}
// 函数定义
// 补足。。。
long long fun(int n){
    long long g=0,f=0; 
    if(n==1){
        g=2;
    }
    else{
        g=2*(fun(n-1)+1);
    }
    f=g-1;
    return f;
}

输出结果：

 

 

 

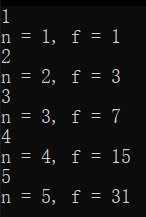
bonus part：

例题：实现2^n-1

 (待补充

 

 

---

 

 

 

 

实验任务五

原始程序：

#include <stdio.h>
void draw(int n, char symbol); // 函数声明
#include <stdio.h>
int main() {
    int n, symbol;
    while(scanf("%d %c", &n, &symbol) != EOF) {
    draw(n, symbol); // 函数调用
    printf("\n");
    }
    return 0;
}
// 函数定义
// 补足代码。。。
void draw(int n, char symbol){
    int st;
    int count=1;
    for(;n>=0;n--){        
        //前半空白 
        for(int i=n;i>0;i--)
            printf(" ");
        //打印字符 
        st=2*count-1;
        count++;
        while(st--){
            printf("%c",symbol);
        }
        //后半空白 
        for(int t=n;t>0;t--)
            printf(" ");
        //换行 
        printf("\n");
        fflush(stdin);    
    }        
}

运行结果：

 

 

 

 

---

 

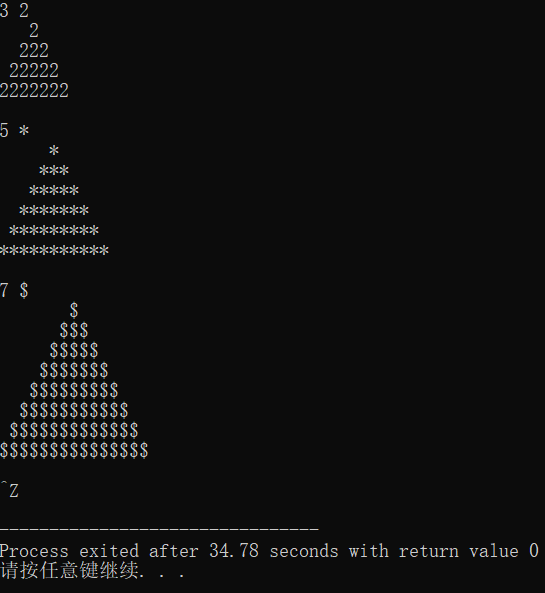
实验总结

说实话我觉得这章和上章的关系太紧密了，函数是这一章的主要内容，我们是学会怎么使用、构造函数，

让它成为我们第三章算法的偷懒工具。递归什么的，函数的亮点在编写程序里还是很能表现出来的。

 

嗯……熟能生巧还是真理，这是减少你调试次数的绝对办法之一。

有一句话不是说没有人能一遍编出完美的程序吗？Linus Torvalds也说

实际上没有人能一次就写出完美的代码,除了我。但是世界上只有一个我。 

 

我尝试用数组和字符串的方法去写实验任务四的bonus part，但是写都写不出来。

现在先vacant，待我日后经验丰富了立刻回头来补足。

 

我认为编码风格、编码规范是很重要的东西，一类东西不应当隔着放，而且应当与不同的类隔行。

养成写开头注释，结尾注释，行注释的习惯。

 

 

 

 

 

 

 

 

Thanks for reading.