基本子串结构

2023 国家集训队论文 xtq《一类基础子串数据结构》阅读笔记。

主要借鉴了 crashed 的学习笔记 和 127 的学习笔记，侵删。

虽然但是这个名字是真的朴素。明明可以取一些好听的名字的。按照翻译应该叫做 \(\text{BSS}\)（Basic Substring Structure）。

本文是阅读笔记，性感理解、口头描述偏多。

引言

是一个用途极其广泛的子串结构。\(\text{SAM}\) 的出现使一类字符串题目对字符串的维护转移到对信息的维护，适配数据结构选手。那 \(\text{BSS}\) 的出现使 \(\text{SAM}\) 转换后对信息的维护又转换成了坐标系模型，适配没脑子的选手。

与 \(\text{BSS}\) 定位相同的还有 DAG 链剖分。一个比一个牢。相较来说应该还是 \(\text{BSS}\) 用的多。

BSS 的基本内容与结构

约定

默认 \(O(|\sum|)=O(1)\)。

拓展串

\(\text{occ}(t)\)：子串 \(t\) 的出现次数。

\(\text{ext}(t)\)：\(t\) 的拓展串，包含 \(t\) 的与 \(t\) 出现次数相同的最长串。

不难证明拓展串存在且唯一。

由拓展串可以给出 \(s\) 子串集合的一个划分。后称等价类即拓展串相同的子串的集合。

\(\text{rep}(a)\)：\(a\) 等价类的代表元，定义其为 \(a\) 里满足 \(t=\text{ext}(t)\) 的 \(t\)。

引理：若左端点对齐的两子串在同一等价类，则将左端点向左平移，对齐的子串依旧在同一等价类。右端点对齐同理。

证明可以考虑左端点对齐的等价类即 \(\text{startpos}\) 等价类，由 \(\text{SAM}\) 性质显然。

坐标系

\(\text{posl}(t),\text{posr}(t)\)：\(t\) 首次出现的位置。

\(G\)：平面直角坐标系，\((x,y)\) 表示 \(\text{posl}=x,\text{posr}=y\) 的子串，不存在就空。

不难证明这是一个阶梯网状图。

这里给出 aababcd 的 \(G\)。直线框起来的是等价类。

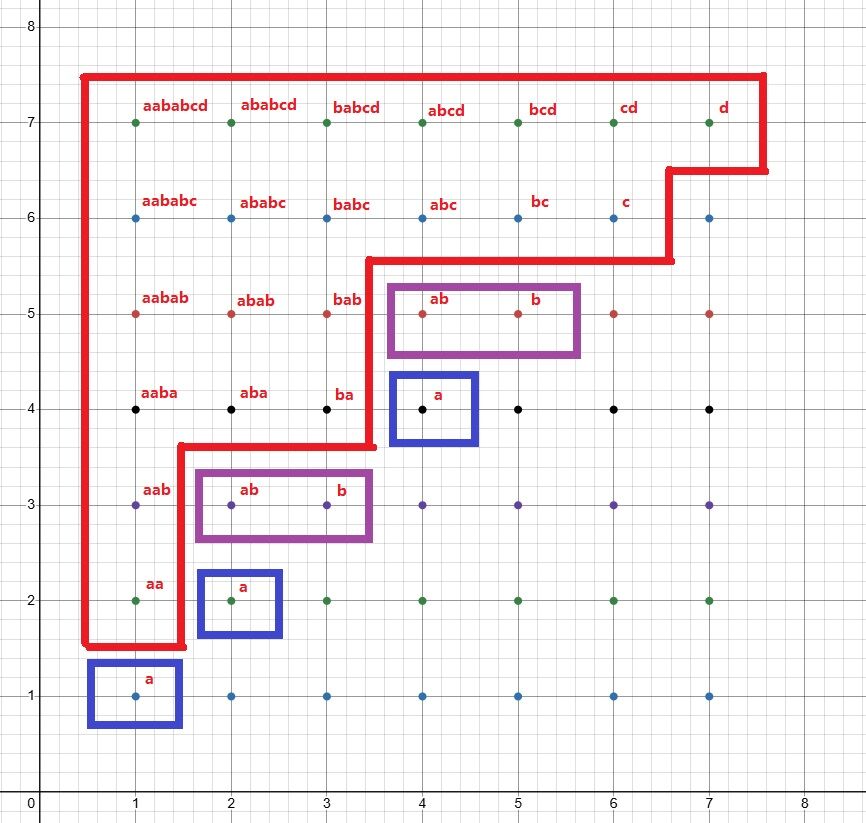
拓展的过程实际上就是向左和向上平移。向左会更新前缀，向上会更新后缀。

等价类对应阶梯状图形，左上角是拓展串。每个阶梯状会出现 \(\text{occ}(\text{ext}(a))\) 次。

Parent Tree

每一行的右端点对齐，每一列的左端点对齐。前者即 \(\text{endpos}\)，后者即 \(\text{startpos}\)，分别对应正串 \(\text{SAM}\) \(T_0\) 和反串 \(\text{SAM}\) \(T_1\) 上的结点。

换句话说，\(T_0\) 的点对应同行等价类，\(T_1\) 的点对应同列等价类。故所有等价类周长 \(O(n)\)。

举个栗子，你可以将 \(G\) 按照行剖开，这时每一行的每一个同属一个等价类的一段都对应一个 \(\text{endpos}\) 等价类，即 \(T_0\) 的结点。

于是 \(G\) 上的连边就很自然了。还是用行举例，按等价类剖开，交界处连边即可。

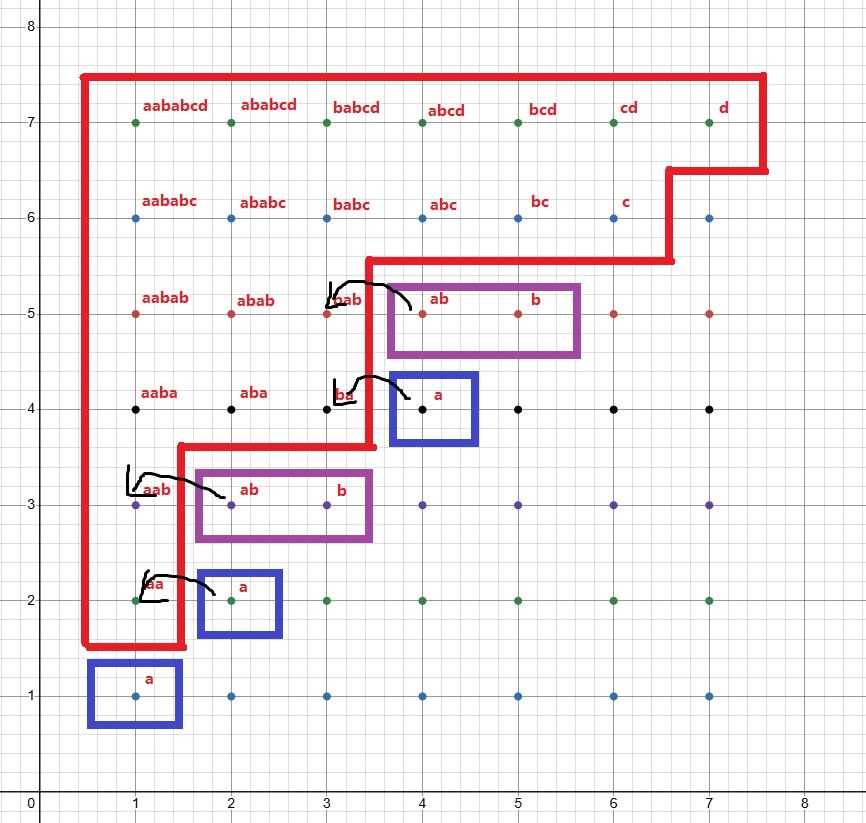
注意这里从右往左，从下往上对应的是树上的从父亲到儿子。

可以看作一个本质不同子串在前后加字符的转移。

然后你还需要考虑不包含代表元的 \(\text{endpos}\) 等价类与 \(\text{startpos}\) 等价类它们与同等价类之间的连边。

有一个引理是这类等价类对应到 \(\text{SAM}\) 上只有一条出边。

换句话说，一个等价类对应到 \(T_0\) 上就是一条除首尾外没有其它边的链。本质就是压缩 \(\text{SAM}\)。

直接按结点倒序构建是对的，因为越上面的 \(\text{endpos}\) 集合越晚形成。

SAM

由引理，一个 \(\text{endpos}\) 等价类不断上移依旧会被某个等价类完全包含，另一边同理。

我们需要将两个 \(\text{SAM}\) 的转移完全对应到 \(G\) 上。

正 \(\text{SAM}\) DAG 出边：对应行 \(\text{endpos}\) 等价类上出边。

正 \(\text{SAM}\) Parent 出边：对应行 \(\text{endpos}\) 等价类左出边。

反 \(\text{SAM}\) DAG 入边：对应列 \(\text{startpos}\) 等价类右出边。

反 \(\text{SAM}\) Parent 入边：对应列 \(\text{startpos}\) 等价类下出边。

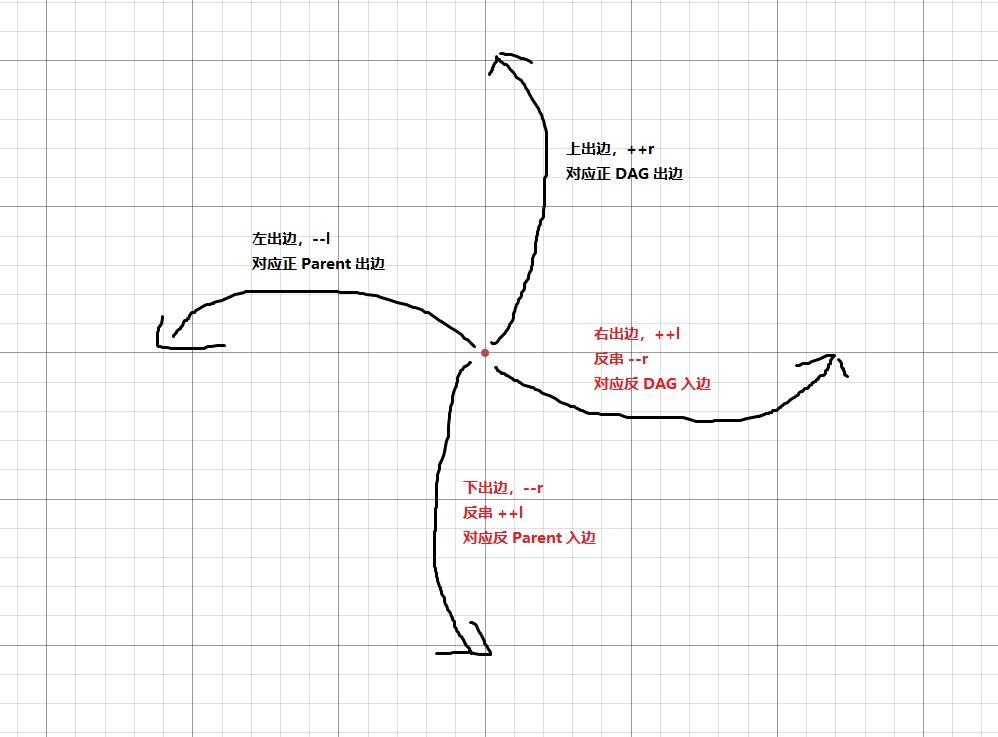
然后注意到一个事实：

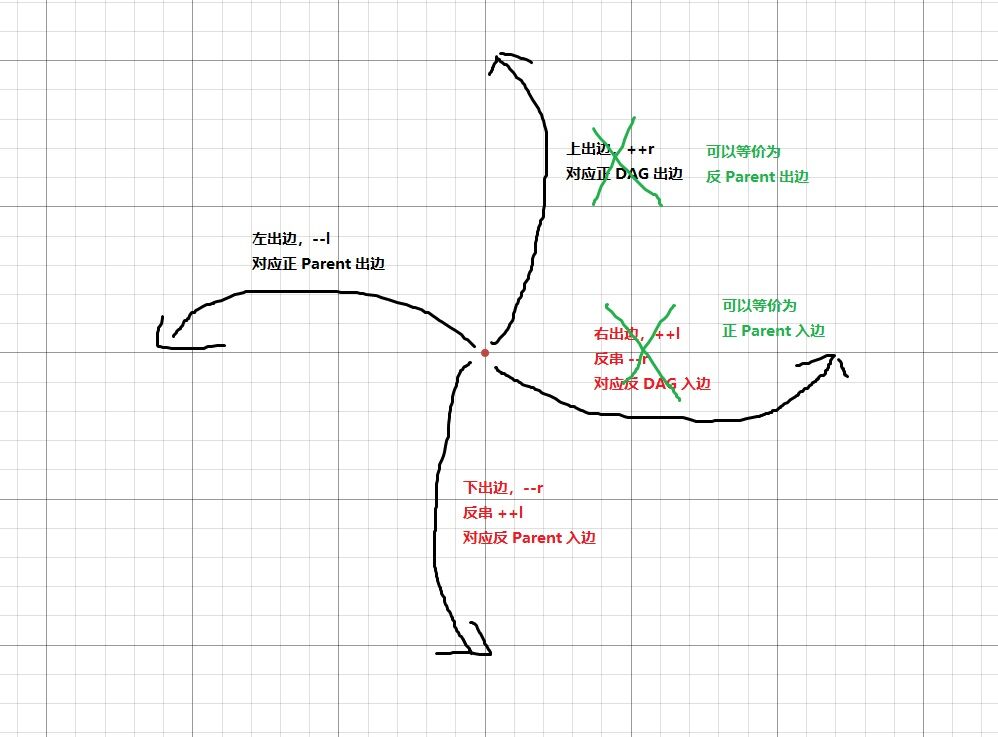
DAG はもう、死んでいる

研究一下这个结构。

前面说过，压缩 \(\text{SAM}\) DAG 上出度为 \(1\) 的点就会变成 \(\text{occ}\) 等价类。

这种关系与正反无关，所以正反串会有一个一一对应。

这就是论文想要表达的内容的具象化展示。

总结

牢记 \(\text{BSS}\) 本质上就是在统一 \(\text{endpos}\) 等价类和 \(\text{startpos}\) 等价类。

同一 \(\text{occ}\) 等价类内部的移动和修改可以快速定位。

具体地做完题再来写。

BSS 的构建

这么美妙的一个结构肯定需要想怎么构造啊。

首先建出正反串 \(\text{SAM}\)。

一个引理是走 DAG 只遍历指向 len+1 节点的边会形成一个树形结构。

考虑这棵树上一条边 \((u,v)\)：

若 \(u,v\) 同属一个等价类，则它们的关系是左对齐，上下移。

否则跳反向边即可。注意跳的时候 \(v\) 相当于向前加字符，它们显然是父子关系，直接在儿子处预处理即可。

代码直接看 127 大佬的就行，他写的真的很好看。

应用

CF1817F Entangled Substrings

注意到 \(acb\) 出现次数与 \(a,b\) 相同，故 \(a,b\) 同属一个等价类。问题就是等价类内部计数。

由阶梯形的美妙性质，可以直接一边双指针一边加入维护。

代码

UOJ577 打击复读

题意：给你字符串，序列 \(wl\) 和 \(wr\)，定义

\[\begin{aligned} vl(s[l...r])&=\sum_{x\in startpos(s[l...r])}wl_x\\ vr(s[l...r])&=\sum_{x\in endpos(s[l...r])}wr_x\\ w(s[l...r])&=vl(s[l...r])\times vr(s[l...r]) \end{aligned} \]

求

\[\sum_{l=1}^n\sum_{r=l}^n w(s[l...r]) \]

多次询问单点修改 \(wl\)。

一个显然的观察是最后结果是一个关于 \(wl\) 的多项式，算出系数即可带修。

\(vl,vr\) 其实就是子树权值和，由于 \(wr\) 不变，\(vr\) 可以预处理。另外，同行等价类 \(vr\) 相等，同列等价类 \(vl\) 相等。

考虑单点贡献为 \(vl(s[l...r])\times vr(s[l...r])\)，由于同列 \(vl\) 相同，我们考虑一列等价类 \(vl(s[l...[r1,r2]])\) 的总系数 \(\sum_{i=r1}^{r2}vr(s[l...i])\)。

你看上面那个柿子，本质上就是连续几行的行等价类的前缀和。

把这个拿回去跑就可以倒推 \(wl\) 的系数了。

阶梯形的性质很多，最常见的就是双指针。

UOJ697 广为人知题

题意：给你一个总串，有 \(m\) 个子串作为模式串，\(q\) 次询问以某个子串作为文本串匹配次数之和。

在 \(G\) 上作转换，实际上就是 \(m\) 个点，\(q\) 次右下角数点。不直接二维数点的原因是 \(m\) 个点是基于一个等价类算一次的。

自然会想，可以尝试对每个等价类计数。

考虑以下划分（这里的计数方法借鉴了 crashed 大佬的）：

我们先求出所有有颜色地方（除了深蓝色）的答案并。

绿色部分和黄色部分的并就是我们需要求的下边的答案。淡蓝色部分就是二维数点。右边的靛蓝就是另一个等价类的答案。

然后差分掉深蓝色右边部分的答案即可。

下边和右边的答案都是可以前缀和预处理的。

一定注意预处理等价类时使用 bfs 而不是 dfs，不然不能保证先右后左。

单 \(\log\) 被卡常了……

终于卡完常了。

BSS 剖分

咕了。