汉诺塔递归调用原理

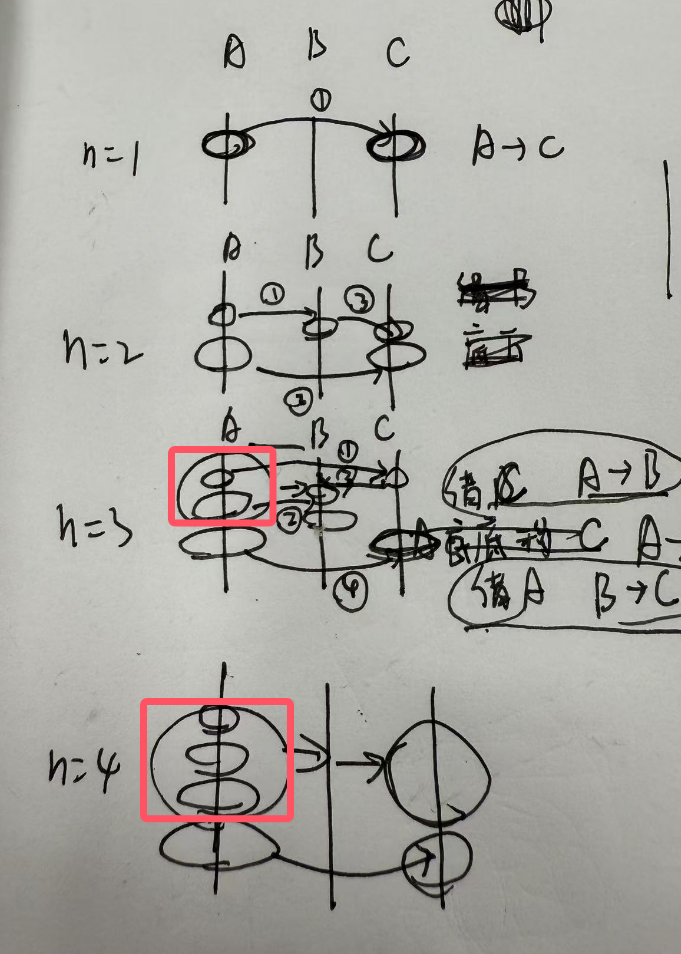
1. n=1时，直接A移动到C
2. n=2时，为了让最底下的最先移动到C，先把压在上面的移动到B，最底下的就可移动到C，再把压在上面的移动到C
   其实n=2时已经隐含了解决问题的方式，压在上面的前n-1个移动到B，第n个移动到C，前n-1个移动到C。
3. n=3时，把前两个移动到B，第三个移动到C，前两个移动到C。这里前两个的移动方式就可以直接使用n=2时的移动方式，只是这次是A->B, n=2是A->C (移动方法是一样的)
4. n=4时，把前三个移动到B，第四个移动到C，前三个移动到C。

每一次的移动方式都利用了上一次移动方式来解决移动盘子难的问题，让复杂问题拆解成一个个小问题。

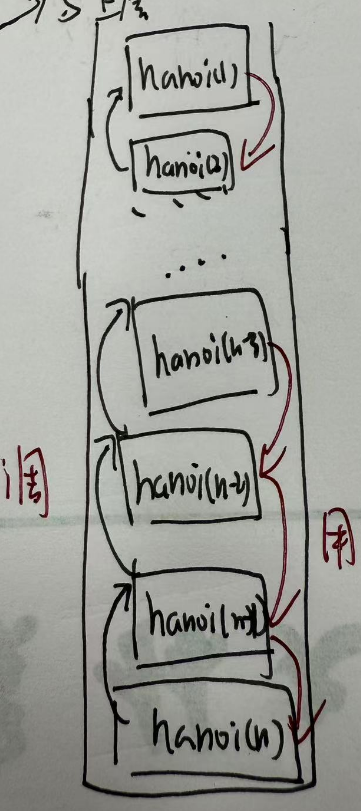
hanoi(n)移动n个碟子问题可拆解为:
将前n-1个碟子移动到空闲的柱子，第n个碟子移动到目标柱子，再将前n-1个碟子移动到目标柱子。而前n-1个碟子移动到空闲的柱子这个动作可通过hanoi(n-1)来实现，直接调用上一次实现过的算法

采用递归调用，即使用栈，先将hanoi(n)推入栈中，再调用hanoi(n-1)推入栈中......直到hanoi(1,A->C)进栈，move(A->C)立即解决直接出栈，hanoi(2,A->C) 压在上面的一个move(A->B)，下面的一个move(A->C),最后move(B->C)解决，hanoi(3,A->C )前两个hanoi(2,A->B), move(A->C),hanoi(2,B->C),.....以此类推。