树上dp
树的存储
邻接表:将这个点的所有直接子节点存储在以这个点为开头的链表上
https://oi-wiki.org/graph/save/#邻接表
void add(int u,int v)// 添加一条边u->v
{
cnt++;
nxt[cnt]=head[u];
head[u]=cnt;
to[cnt]=v;
}
void solve(int u)
{
f[u][1]=h[u];
for (int i = head[u]; ~i; i = nxt[i])
{ // ~i 表示 i != -1
int v = to[i];
}
}
memset(head,-1,sizeof head);
换根dp
代码源 距离和
size[i]表示以i为根的子树上有多少个点,f[i]表示i到子树中其他所有点的距离和
size[i]=∑size(j)+1 j∈son(i)
假设j是i的直接儿子,以j为根的子树对i的贡献为f[j]+size[j]
f[i]=∑(f[j]+size[j])=∑(f[j])+size[i]-1
v[i]表示i点的父亲作为它子树时对i号点的贡献
当i号点作为父亲时 ,1号点作为子树时提供的贡献
v[i]=f[1]-f[i]-size[i]+n-size[i]
f[1]-f[i]-size[i]表示除去i号点及其子树剩下的部分
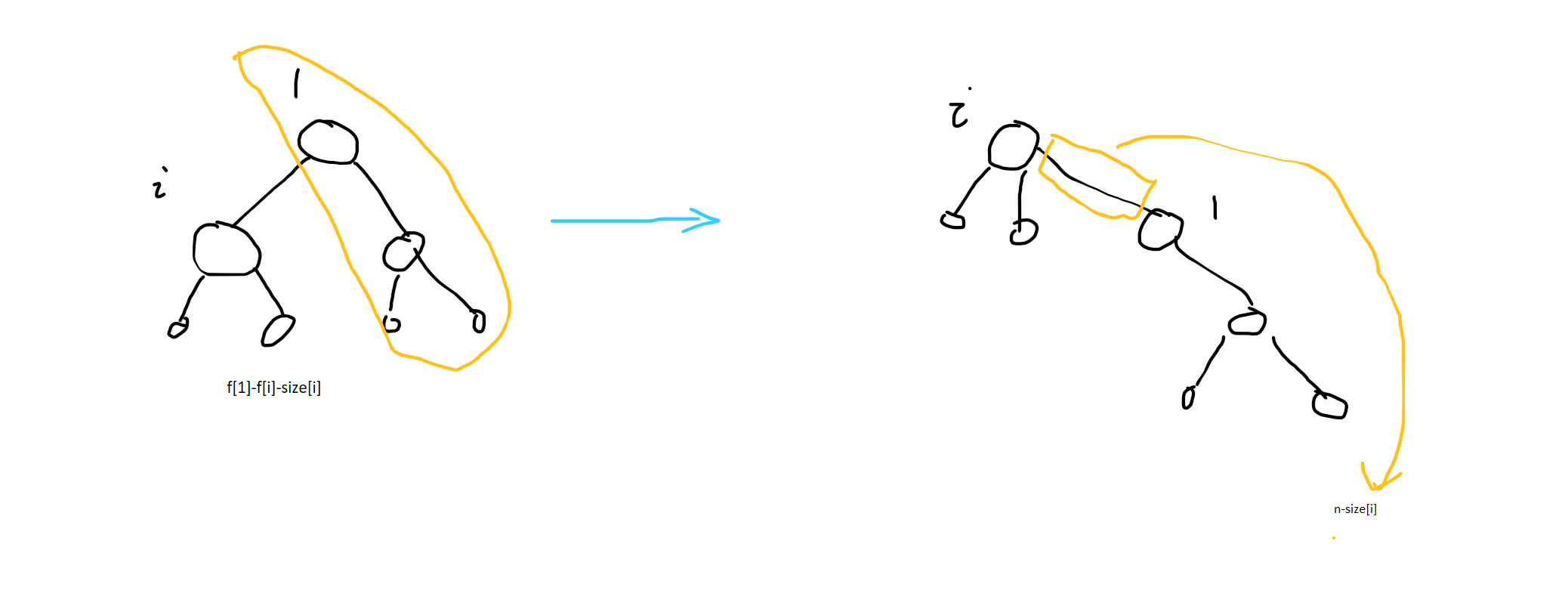
当根从x变成儿子y时
v[y]=v[x]+f[x]-f[y]-size[y]+n-size[y]//
v[x]+f[x] x为根时所有点到他的距离和
f[y]+size[y] y为子树时的贡献
n-size[y] x子树中点的个数
代码
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10;
int nxt[N],head[N],to[N];
int cnt=-1;
#define rep(i,a,n) for(int i=a;i<=n;i++)
int sz[N],f[N],v[N];//节点数,所有子树中的边数和,父节点变成子节点后的贡献
bool b[N];
int n;
void add(int u, int v) {// 添加一条边u->v
nxt[++cnt] = head[u]; // 当前边的后继
head[u] = cnt; // 起点 u 的第一条边
to[cnt] = v; // 当前边的终点
}
void up(int u)
{
sz[u]=1;
b[u]=true;
for(int i=head[u];~i;i=nxt[i])
{
int v=to[i];
if(!b[v])
{
up(v);
sz[u]+=sz[v];
f[u]+=f[v];
}
}
f[u]+=sz[u]-1;
}//size f
void down(int u)
{
b[u]=true;
for(int i=head[u];~i;i=nxt[i])
{
int v2=to[i];
if(!b[v2])
{
v[v2]=v[u]+f[u]-f[v2]-sz[v2]+n-sz[v2];
down(v2);
}
}
}//v
int main()
{
cin>>n;
memset(head,-1,sizeof head);
rep(i,1,n-1)
{
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
memset(b,false,sizeof b);
up(1);
memset(b,false,sizeof b);
down(1);
rep(i,1,n)cout<<v[i]+f[i]<<endl;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号