FM+DNN模型融合 / FM及其变形

　　FM模型想必大家都不陌生，在排序模型刚起步的年代，FM很好地解决了LR需要大规模人工特征交叉的痛点，引入任意特征的二阶特征组合，并通过向量内积求特征组合权重的方法大大提高了模型的泛化能力。但标准FM的缺陷也恰恰是只能做二阶特征交叉，所以与DNN结合可以帮助我们捕捉特征之间更复杂的非线性关系。实际上，强如DIN这类的深度学习模型，在实际业务场景中，往往也要结合LR等简单模型联合训练才能在线上拿到正向收益。
　　我们先来简单回顾下FM模型。

FM

　　 

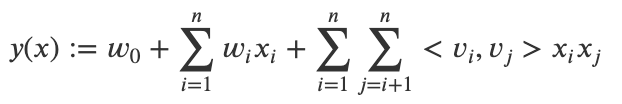
　　FM函数形式如上图所示。

　　FM 模型直接引入任意两个特征的二阶特征组合。对于每个特征，FM学习一个大小为k的一维向量，任意两个特征组合的权重值，通过特征对应的向量的内积来求出。

　　这么做的好处就是，即使两个特征从来没有同时在训练样本中出现过，我们也可以通过计算他们的向量的内积来得到他们组合的权重。因为FM是学习单个特征的embedding，并不依赖某个特定的特征组合是否出现过，所以只要特征x_i和其它任意特征组合出现过，那么就可以学习自己对应的 embedding 向量。
　　此外，我们可以通过对二阶部分化简，使其时间复杂度降到线性时间，使其满足工业化需求。化简过程如下，分步骤化简参考优雅的FM。

 

　　讲到这里，FM模型堪称优雅，但它并不完美，仍有自己的缺陷。

　　首先，FM只能做二阶特征交叉，无法捕捉特征之间更复杂的非线性关系；其次，当某个特征与其他特征做交叉时，都是用同样的向量去做计算。但是不同特征之间的交叉，重要程度是不一样的。例如用户性别特征和商品性别做交叉，相较于与商品点击率特征做交叉要更有价值。所以我们希望借助DNN模型发挥二者的优势，得到更优秀的模型。

　　那FM怎么与DNN结合呢？

　　FM为每个特征都学习一个大小为k的一维向量，这本质上是在对特征进行向量化表示，和现在各种实体embedding的思想是一致的。而且观察FM公式中的二阶部分，不考虑最外层的求和，可以得到一个K维的向量。所以可以将FM二阶部分得到的向量或对二阶部分的计算做特殊处理之后作为DNN的输入。根据结合方式的不同，又可以分为以下两种结构：
　　（1）并行结构：代表模型deepFM；
　　（2）串行结构：代表模型NFM、AFM。

　　下面将会对这些模型一一做介绍。

FNN

　　一句话介绍：使用FM隐向量作为DNN模型embedding的初始化值。
　　FNN可以看作FM与DNN的串行结构，其核心思想也很简单，这里就不多做介绍了。

NFM

　　NFM模型的预测公式如下：

　　

 

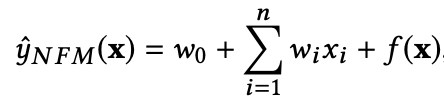
　　其中，f(x)是用来建模特征之间交互关系的多层前馈神经网络模块，架构图如下：

　　

 

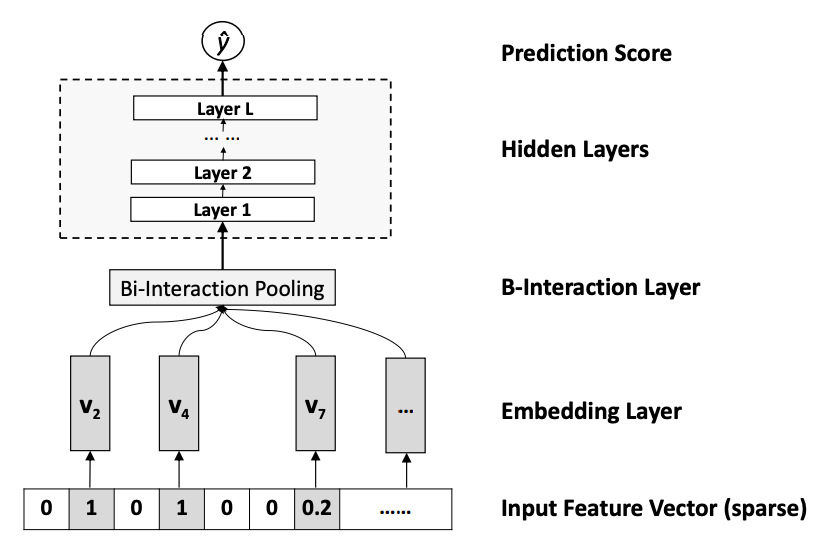
　　Embedding Layer和我们之间几个网络是一样的，embedding 得到的vector就是我们在FM中要学习的隐变量v。
　　B-Interaction Layer其实它就是计算FM中的二次项的过程。前面提到过，对于FM二阶部分化简结果，如果不考虑最外层的求和，可以得到一个K维的向量，即下图中的红框内的部分。

 　　

 

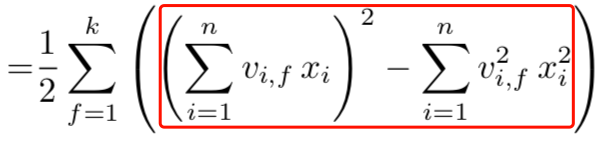
 　　红框部分即为下式，最终结果是一个k维的向量：

　　

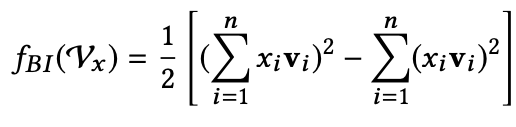
　　Hidden Layers就是我们的DNN部分，将B-Interaction Layer得到的结果接入多层的神经网络进行训练，从而捕捉到特征之间复杂的非线性关系。

　　在进行多层训练之后，将最后一层的输出求和同时加上一次项和偏置项，就得到了我们的预测输出：

　　

　　

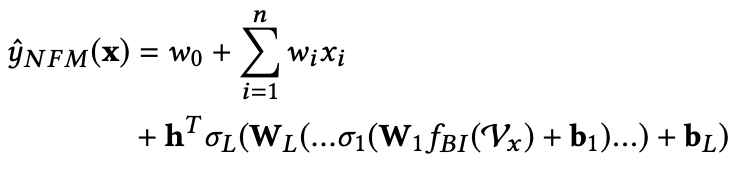
　　我们知道在FM模型中，当某个特征与其他特征做交叉时，都是用同样的向量去做计算。但是不同特征之间的交叉，重要程度是不一样的。那如何体现这种重要度呢？有以下两个方法：
　　（1）FFM
　　（2）attention 机制
　　FFM并不属于FM与DNN结合的模型，不过这里还是简单介绍下。

FFM

　　在 FFM 中，每一个特征x_i，针对其他特征的每一种field f_j，都会学习一个隐向量 v_i,fj。也就是说，隐向量不仅和特征相关，也和field相关。什么是field？举例来说，在排序模型中我们通常会对“国别”这类的离散特征做哑编码，即one-hot，那么“国别”就是一个field，经过也编码之后得到的多个特征同属于“国别”这个field。

　　在 FM 模型中，每一维特征的隐向量只有一个；在 FFM 模型中，假设样本的 n个特征属于 f 个field，那么 FFM 的二次项有 nf个隐向量。FM 可以看作 FFM 的特例，是把所有特征都归属到一个field时的 FFM 模型。
　　FFM模型方程如下：

　　

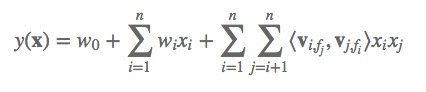
　　可以看到，如果隐向量的长度为 k，那么FFM的二次参数有 n*f*k 个，远多于FM模型的 nk个。
　　此外，由于隐向量与field相关，FFM二次项并不能够化简，其预测复杂度是 O(kn^2)。

AFM

　　AFM之前也有做过介绍，详细参见 Attention在推荐系统中的应用。

　　AFM就是在FM模型的基础上添加了Attention机制。模型目标函数如下：

　　  

　　圆圈中有个点的符号表示哈达玛积，即逐点相乘。两个向量求哈达玛积得到的还是一个向量。

　　a_ij是Attention层输出的权重值，取值范围在[0,1]。

　　现在求和之后得到的是一个K维的向量，还需要再跟一个向量 p 相乘，得到一个具体的数值。

　　从FM和AFM的函数形式容易看出， AFM 的前两部分（即一阶部分）和 FM 相同，二阶部分的网络结构如下：

　　图中的前三部分：sparse iput，embedding layer，pair-wise interaction layer，都和FM是一样的。

　　embedding layer 得到的vector其实就是我们在FM中要学习的隐变量 v 。

　　Attention 层的计算方式如下，也就是使用多层感知机的方式计算权重： 

 　　 

　　

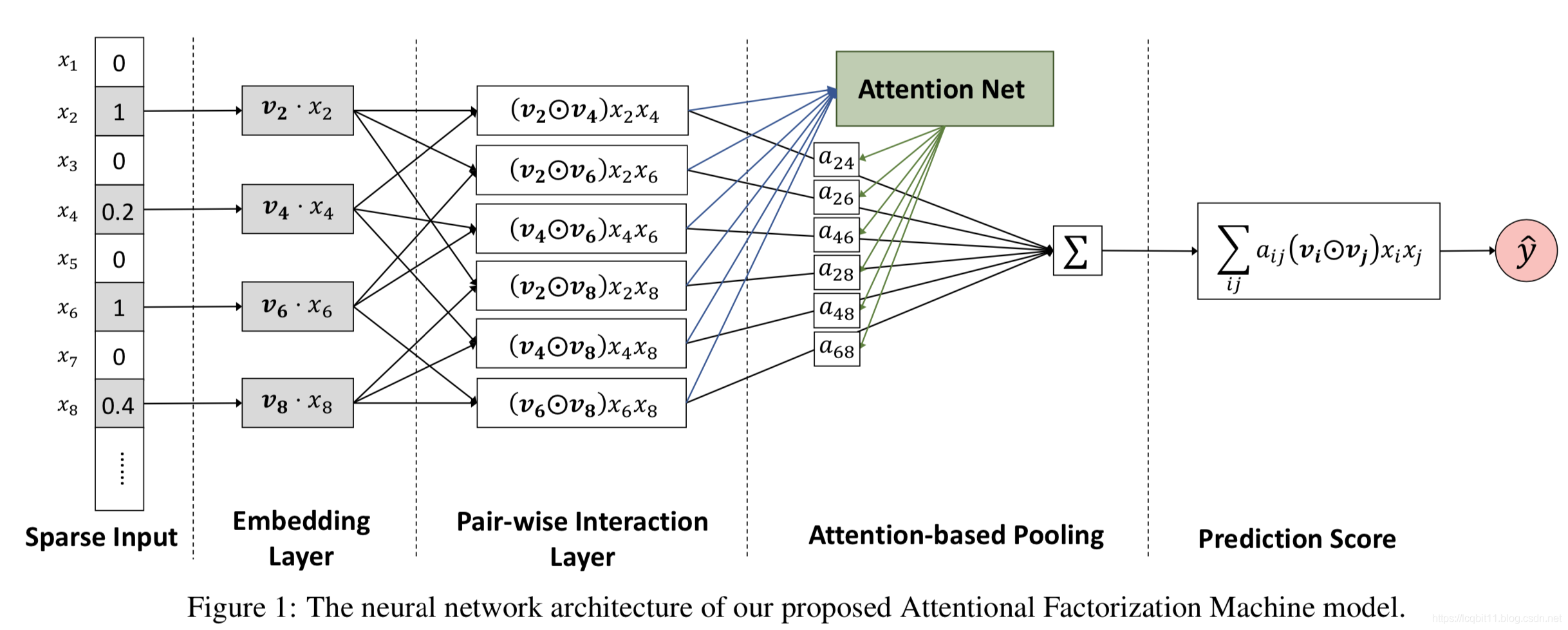
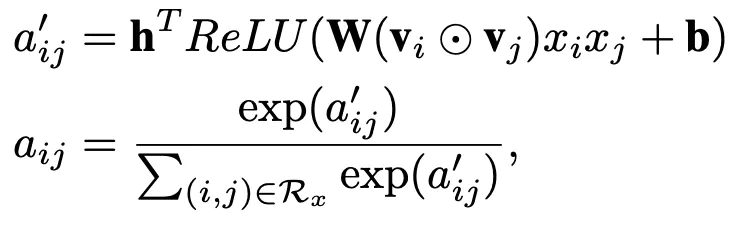
　　以上的模型，都是FM都是以串行结构与DNN结合，下面要介绍的deepFM则是经典的并行结构。 

deepFM

　　deepFM在Wide & Deep结构框架基础上，使用 FM 取代Wide部分的LR。这么做的好处是，WDL模型wide部分仍然需要人工特征工程，deepFM则可以将工程师从特征工程中解放出来。

 　　模型结构图如下：

　

　　

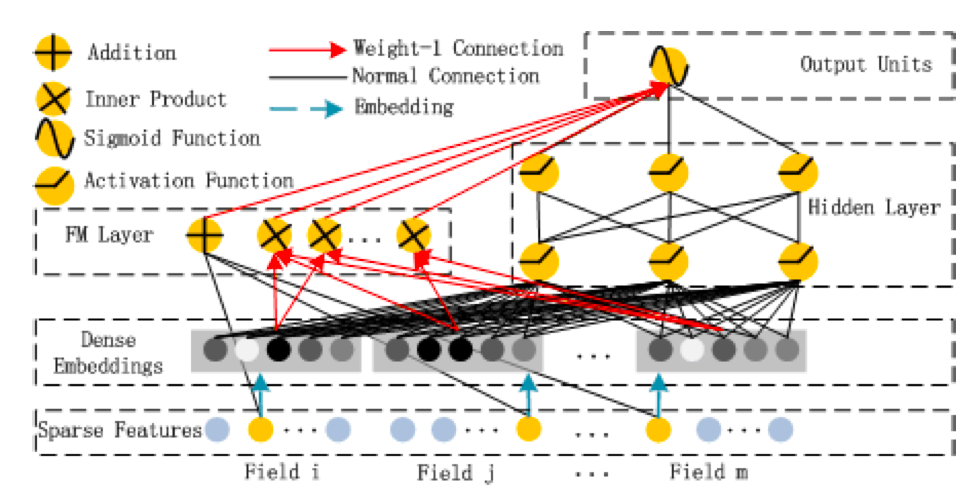
　　模型包含两部分：因子分解机部分与神经网络部分，分别负责低阶特征的提取和高阶特征的提取；需要注意的是FM层 与 NN层 共享相同特征的 embedding。这么做有以下两个优点：
　　（1）降低模型复杂度；
　　（2）在embedding的学习中同时接收与来自低阶、高阶组合部分的反馈，从而学到更好的特征表示。

xDeepFM

　　其实xDeepFM严格来讲并不属于FM与DNN结合的模型，xDeepFM是DCN模型的扩展版本。

　　DCN 的Cross层虽然可以显示自动构造高阶特征，但它是以元素级（bit-wise）的方式。xDeepFM的动机，则是在DCN模型的基础上，将FM的vector-wise的思想引入Cross部分。其模型整体架构如下：

　　本篇博客不对xDeepFM做更多介绍，不过需要指出的是，FM和xDeepFM之间的关系是，如果CIN（xDeepFM的核心部分）只有1层，且加和的权重矩阵恒等于1，那么sum pooling的输出结果，就是一系列的两两向量内积之和，即标准的FM。