优雅的FM

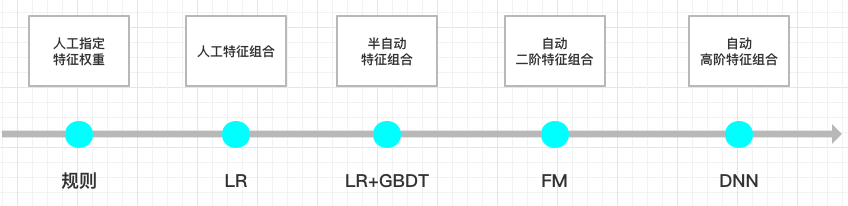
    纵观排序模型的发展过程，我们会发现，特征工程及特征组合的自动化，一直是推动排序模型前进的最主要的方向。例如早期比较成功的LR模型，通过人工特征工程引入非线性。LR之后，就是LR+GBDT，具体做法就是对GBDT每棵树的叶子节点做哑编码之后输入到LR模型中，这时候每棵树的叶子节点的含义，就相当于一种特征组合，所以相比LR，我们说LR+GBDT可以半自动化地做一些特征组合。再发展到后来的FM模型和深度学习模型已经可以做一些二阶或高阶自动化特征组合了。不过既然今天的主题是FM模型，我们还是来看一下FM模型是在什么背景下提出来的。
    我们常常诟病LR模型的人工特征组合费时费力，而且不能穷举所有的特征组合，具体要对哪些特征做交叉完全依赖我们对业务的理解。那么能否将特征组合的能力体现在模型层面呢？于是，有人就提出了一个改进版的线性模型。模型表达式如下：

\[y(x):=w_0+ \sum_{i=1}^{n}w_ix_i+ \sum_{i=1}^{n}\sum_{j=i+1}^{n}w_{i,j}x_ix_j \]

    改进的地方是在LR的计算公式里加入了二阶特征组合，将任意两个特征进行组合，然后把组合出的特征看作一个新特征，融入线性模型中。这种改进的优势是直接将所有的两两组合特征引入模型，不需要人工去做交叉了，哪些组合有用哪些没用让模型自己去学。但是它有个潜在的问题：就是模型的泛化能力很弱。因为要学习组合特征的权重，要求这两个特征必须同时在训练样本里出现过一次。这在CTR预估这种大规模稀疏特征的场景里是很不现实的。
    基于这个问题，我们的FM模型闪亮登场了：

\[y(x):=w_0+ \sum_{i=1}^{n}w_ix_i+ \sum_{i=1}^{n}\sum_{j=i+1}^{n}<v_i,v_j>x_ix_j \]

    FM模型也直接引入任意两个特征的二阶特征组合，但是和上面改进后的线性模型最大的不同，在于特征组合权重的计算方法。FM对于每个特征，学习一个大小为\(k\)的一维向量，于是，两个特征\(x_i\)和 \(x_j\)的特征组合的权重值，通过特征对应的向量\(v_i\)和\(v_j\)的内积<\(v_i\),\(v_j\)>来表示：

\[<v_i,v_j>:=\sum_{f=1}^{k}v_{i,f}·v_{j,f} \]

    这么做的好处就是，即使两个特征从来没有同时在训练样本中出现过，我们也可以通过计算他们的向量的内积来得到他们组合的权重。因为FM是学习单个特征的embedding，并不依赖某个特定的特征组合是否出现过，所以只要特征 xi 和其它任意特征组合出现过，那么就可以学习自己对应的embedding向量。这本质上是在对特征进行向量化表示，和现在各种实体embedding的思想是一致的。理论介绍到这里，只能用优雅两个字来形容。
    如果FM模型只推导到这里的话，它还没办法进入到工业应用阶段。我们可以计算一下FM表达式二阶部分在预测阶段的时间复杂度，不难得到为\(O(k*n^2)\)。这个时间复杂度对于需要在毫秒级时间响应的排序场景来说是难以接受的。但是如果FM模型仅仅到这种程度的话也称不上优雅二字了。作者在论文中指出，通过对FM的公式进行改写，可以将其时间复杂度降到线性时间，改写过程如下：

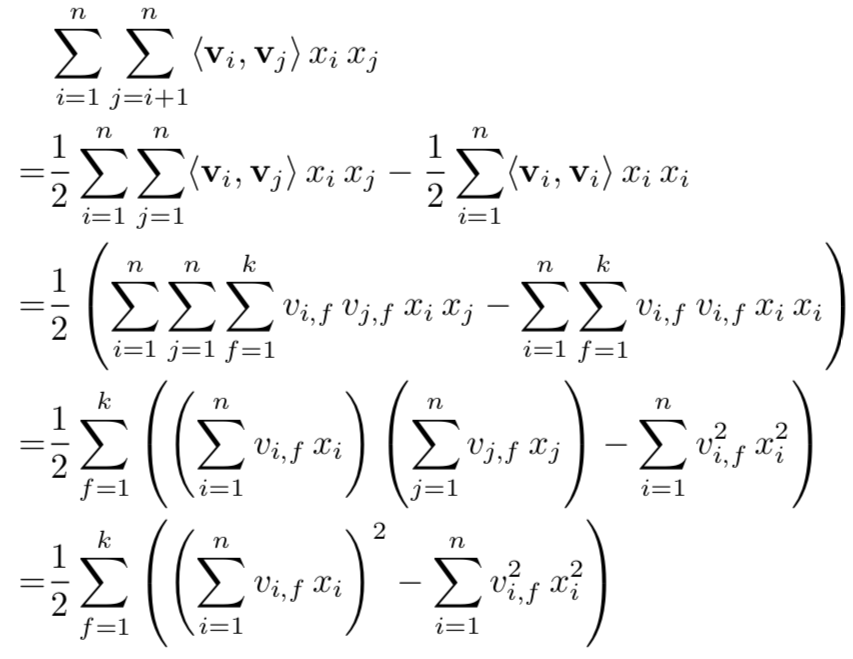
    初看这个改写过程时真的是头皮发麻。不过分解步骤来看的话，还是很好理解的。

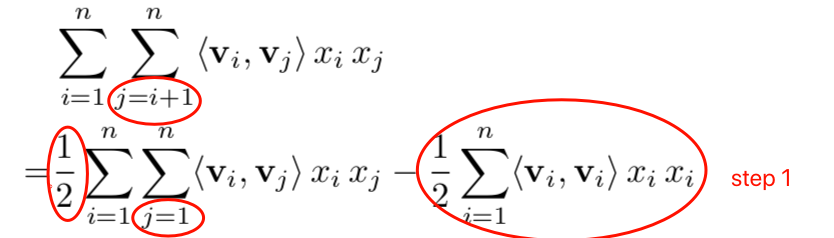
    先来看第一步改写的地方，和原来的公式相比，有了三处变化：
    首先原式第二个\(\sum\)的下标由\(j=i+1\)改写成了\(j=1\)，这么改写之后，原来是不需要计算\(<v_i,v_i>\)的，现在也计算了进来，所以这部分要减掉；其次原来只需要计算\(<v_i,v_j>\)，现在把\(<v_j,v_i>\)也计算了一遍，所以要除以\(2\)。也许有人会疑惑为什么\(step1\)的后面部分也要除以\(2\)，其实把公式换成下面这样会更好理解一点。

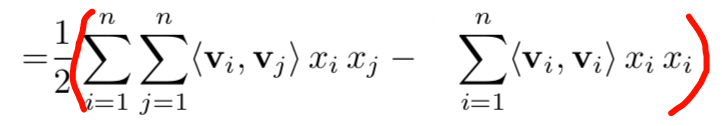
    如果还有疑问的话，可以假设只有两个特征的情况代入公式试一下。

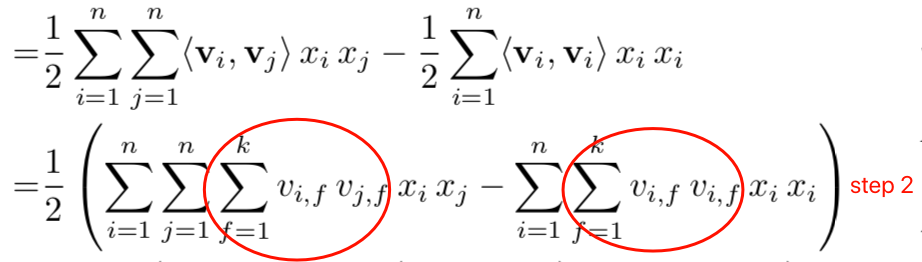
    第二步就比较简单了，不过是把\(<v_i,v_i>\)的展开式带入了进来，然后提了个公因子\(1/2\).

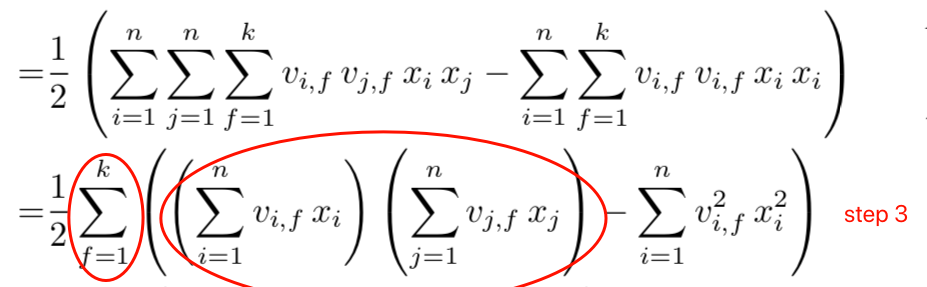
    第三步改写，前半部分很好理解，就是提了个公因子。中间不分可能不太好理解，也就是如下图所示，怎么从前面的表达式变换到后面。

    我们仔细观察\(\sum_{i=1}^{n}\sum_{j=1}^{n}v_{i,f}v_{j,f}x_ix_j\)这个表达式，两个\(\sum\)也就是两层循环，我们先限定外部循环也就是令\(i=1\)，把\(i=1\)带入到后面\(\sum\)的循环中，展开后即为下式：

\[v_{1,f}x_1*v_{1,f}x_1+v_{1,f}x_1*v_{2,f}x_2+…+v_{1,f}x_1*v_{n,f}x_n \]

    提取公因子\(v_{1,f}x\_1\):

\[v_{1,f}x_1*(v_{1,f}x_1+v_{2,f}x_2+…+v_{n,f}x_n)=v_{1,f}x_1*\sum_{j=1}^{n}v_{j,f}x_j \]

    令\(i=2...n\)，即如下所示:

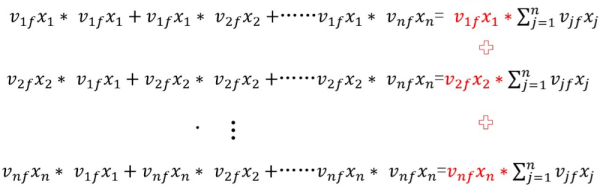
    再提取一次公因子\(\sum_{j=1}^{n}v_{j,f}x_j\)，就得到\((\sum_{i=1}^{n}v_{i,f}x_j)(\sum_{j=1}^{n}v_{j,f}x_j)\).

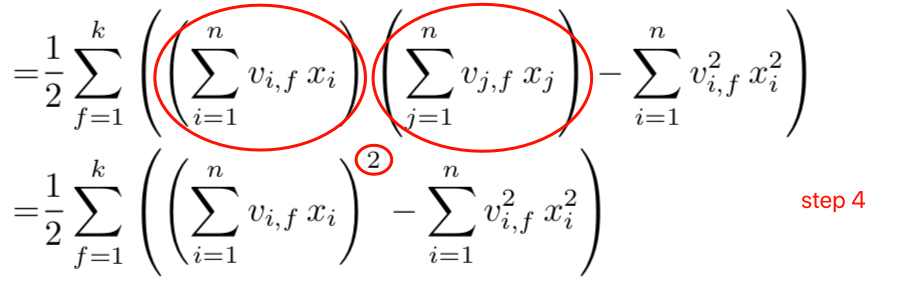
    最后一步改写，\(step3\)改写后圈起来的两部分，只是下标的表示不同，但都是求和，值也相同，所以可以改为平方。
    经过改写之后，神奇的一幕出现了，改写后表达式时间复杂度变成了\(O(k*n)\)，就两个字：优雅。