行列式计算的归纳
线性代数真难,而且这个学期就要结课。学到现在(矩阵的分块),个人感觉最难的还是行列式的计算。哎哎。不过好在这些东西很有套路性,经过一番学习后,我就来总结一下——
行列式的分类
第一类 范德蒙德行列式
\({D_n} = \left| {\begin{array}{*{20}{c}} {{a_1}^0}&{{a_2}^0}& \cdots &{{a_n}^0}\\ {{a_1}^1}&{{a_2}^1}&{}&{{a_n}^1}\\ \vdots &{}&{}& \vdots \\ {{a_1}^{n - 1}}&{{a_2}^{n - 1}}& \cdots &{{a_n}^{n - 1}} \end{array}} \right|\)
这个行列式的特点:某元素若是\(x\)次幂,那么它下方的那个元素(若存在)就是\(x+1\)次幂。
为了消去这个\(x\)与\(x-1\)的差距,不妨试试每一行减去上一行元素乘以\(a_1\)
\({D_n} = \left| {\begin{array}{*{20}{c}} 1&1& \cdots &1\\ 0&{{a_2} - {a_1}}&{}&{{a_n} - {a_1}}\\ 0&{{a_2}({a_2} - {a_1})}&{}&{{a_n}({a_n} - {a_1})}\\ \vdots &{}&{}&{}\\ 0&{{a_2}^{n - 2}({a_2} - {a_1})}&{}&{{a_n}^{n - 2}({a_n} - {a_1})} \end{array}} \right|\)
按第一列展开
\({D_{n - 1}} = \left| {\begin{array}{*{20}{c}} & {{a_2} - {a_1}}& \cdots &{{a_n} - {a_1}}& \\ & {{a_2}({a_2} - {a_1})}&{}&{{a_n}({a_n} - {a_1})}& \\ & \vdots &{}&{}& \\ & {{a_2}^{n - 2}({a_2} - {a_1})}&{}&{{a_n}^{n - 2}({a_n} - {a_1})}& \end{array}} \right|\)
提取公因式
\({D_{n - 1}} = ({a_2} - {a_1}) \cdots ({a_n} - {a_1})\left| {\begin{array}{*{20}{c}} & {1}& \cdots &{1} \\ & {{a_2}}&\cdots&{{a_n}}& \\ & \cdots &\cdots&\cdots{} & \\ & {{a_2}^{n - 2}}&{\cdots}&{{a_n}^{n - 2}}& \end{array}} \right|\)
一直循环这个过程,直到行列式被彻底化干净,得到
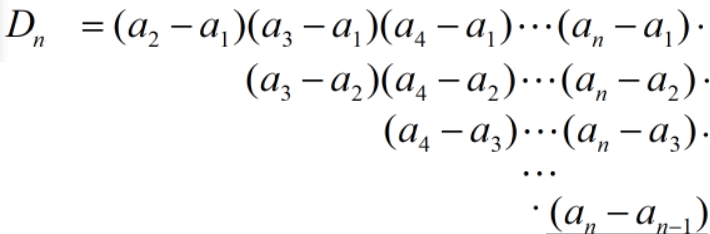
也就是
\({D_n} = \prod\limits_{1 \le j < i \le n}^{} {({a_i} - {a_j})}\)
第二类 双对角线行列式
\({D_n} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{b_1}}&{}&{}&{}\\ {}&{{a_2}}&{{b_2}}&{}&{}\\ {}&{}&{{a_3}}&{{b_3}}&{}\\ {}&{}&{}& \cdots &{\cdots}\\ {{b_n}}&{}&{}&{}&{{a_n}} \end{array}} \right|\)
形如这种,主对角线以及紧挨着主对角线的那一条线(即次对角线)上有非零元素,还有一个非零元素被挤到角落(为什么有一个元素被挤到角落了?因为如果没有这个被挤到角落的元素话,这个行列式就是个三角行列式,太好算了hhh),其它所有元素都为0。
解法:只需给第一列展开即可。特别注意\(\prod\limits_{i = 1}^n {{b_i}}\)的符号!
\({D_n} = \prod\limits_{i = 1}^n {{a_i} + {{( - 1)}^{n + 1}}\prod\limits_{i = 1}^n {{b_i}} }\)
第三类 箭头行列式(爪型行列式)
此类行列式以形状酷似箭头而得名。下面是一个箭头行列式。
\(D_n =\left| {\begin{array}{*{20}{c}} {x1}&p&p& \cdots &p\\ q&{x2}&{}&{}&{}\\ q&{}&{x3}&{}&{}\\ \vdots &{}&{}& \ddots &{}\\ q&{}&{}&{}&{xn} \end{array}} \right|\)
要计算这种行列式,只需设法将箭头的任意一侧消去,得到一个三角行列式后即可快速计算。
现在以消去左箭头,即第一列为例:
若想消去第一列的第二个元素q,则将第二列整体乘以\(-\frac{q}{x2}\)后加到第一列,得到
\(D_n =\left| {\begin{array}{*{20}{c}} {x1 + p( - \frac{q}{{x2}})}&p&p& \cdots &p\\ 0&{x2}&{}&{}&{}\\ q&{}&{x3}&{}&{}\\ \vdots &{}&{}& \ddots &{}\\ q&{}&{}&{}&{xn} \end{array}} \right|\)
若想消去第一列的第三个元素q,则将第三列整体乘以\(-\frac{q}{x3}\)后加到第一列,得到
\(D_n =\left| {\begin{array}{*{20}{c}} {x1 + p( - \frac{q}{{x2}})+p( - \frac{q}{{x3}})}&p&p& \cdots &p\\ 0&{x2}&{}&{}&{}\\ 0&{}&{x3}&{}&{}\\ \vdots &{}&{}& \ddots &{}\\ q&{}&{}&{}&{xn} \end{array}} \right|\)
这个操作重复多次,直到得到上三角行列式
\(D_n =\left| {\begin{array}{*{20}{c}} {x1 - pq\sum\limits_{i = 2}^n {_{}} \frac{1}{{xi}}}&p&p& \cdots &p\\ {}&{x2}&{}&{}&{}\\ {}&{}&{x3}&{}&{}\\ {}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{xn} \end{array}} \right|\)
解得
\(Dn = (x1 - pq\sum\limits_{i = 2}^n\frac{1}{{xi}})\prod\limits_{i = 2}^n {xi}\).
第四类 两三角型行列式
\(D_n = \left| {\begin{array}{*{20}{c}} {x1}&b&b& \cdots &b\\ a&{x2}&b& \cdots &b\\ a&a&{x3}& \cdots &b\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a&a&a& \cdots &{xn} \end{array}} \right|\)
两三角形行列式就像所有的0都被填满了的上三角和下三角行列式。主对角线上下的元素都分别为\(a\)和\(b\)
1.当\(a=b\)时:
\(D_n = \left| {\begin{array}{*{20}{c}} {x1}&a&a& \cdots &a\\ a&{x2}&a& \cdots &a\\ a&a&{x3}& \cdots &a\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a&a&a& \cdots &{xn} \end{array}} \right|\)
如果能把主对角线下(或者上)方的所有a消去,得到一个箭头行列式,再套用上面的方法,那么问题便可解决。
要想消去\(a\)得到\(0\),经过观察发现,第二列及其之后的所有列的第一个元素都是\(a\),那么让从第二行开始的每一行都减去第一行即可。得到
\(D_n = \left| {\begin{array}{*{20}{c}} {x1}&a&a&a&a\\ {a - x1}&{x2 - a}&{}&{}&{}\\ {a - x1}&{}&{x3 - a}&{}&{}\\ \cdots &{}&{}& \ddots &{}\\ {a - x1}&{}&{}&{}&{xn} \end{array}} \right|\)
化成箭头行列式:
\(D_n = \left| {\begin{array}{*{20}{c}} {x1 + a(x1 - a)\sum\limits_{i = 2}^n {\frac{1}{{xi - a}}} }&a&a&a&a\\ 0&{x2 - a}&{}&{}&{}\\ 0&{}&{x3 - a}&{}&{}\\ \vdots &{}&{}& \ddots &{}\\ 0&{}&{}&{}&{xn} \end{array}} \right|\)
解得\(Dn=[x1 + a(x1 - a)\sum\limits_{i = 2}^n {\frac{1}{{xi - a}}}]\prod\limits_{i = 2}^n {(xi-a)}\)
2.当\(a≠b\)时
\(D_n = \left| {\begin{array}{*{20}{c}} {x1}&b&b& \cdots &b\\ a&{x2}&b& \cdots &b\\ a&a&{x3}& \cdots &b\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a&a&a& \cdots &{xn} \end{array}} \right|\)
采用拆行法,将最后一列拆掉
\(D_n = \left| {\begin{array}{*{20}{c}} {x1}&b&b& \cdots &b+0\\ a&{x2}&b& \cdots &b+0\\ a&a&{x3}& \cdots &b+0\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a&a&a& \cdots &{a + xn - b} \end{array}} \right|\)
\(D_n = \left| {\begin{array}{*{20}{c}} {x1}&b&b& \cdots &b\\ a&{x2}&b& \cdots &b\\ a&a&{x3}& \cdots &b\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a&a&a& \cdots &a \end{array}} \right| + \left| {\begin{array}{*{20}{c}} {x1}&b&b& \cdots &0\\ a&{x2}&b& \cdots &0\\ a&a&{x3}& \cdots &0\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a&a&a& \cdots &{xn - b} \end{array}} \right|\)
等式右侧第一个行列式,我们把它的每一列都减去最后一列从而让最后一行只剩下最后一个元素以便于按行展开,第二个行列式我们直接按最后一列展开。
\(D_n = \left| {\begin{array}{*{20}{c}} {x1 - b}&0&0& \cdots &b\\ {a - b}&{x2 - b}&0& \cdots &b\\ {a - b}&{a - b}&{x3-b}& \cdots &b\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0&0&0& \cdots &a \end{array}} \right| + ({x_n} - b){D_{n - 1}}\)
\(D_n = a({x_1} - b)({x_2} - b) \cdots ({x_{n - 1}} - b) + ({x_n} - b){D_{n - 1}}\)
即\(D_n = a\prod\limits_{i = 1}^{n - 1} {({x_i} - b)}+ ({x_n} - b){D_{n - 1}}\)
我们得到了很简洁的递推公式,可是后面带了一项\(D_{n-1}\)怎么办啊?不妨把这个行列式转置一下,得到:
\(D_n = b\prod\limits_{i = 1}^{n - 1} {({x_i} - a)}+ ({x_n} - a){D_{n - 1}}\)
把这两个式子联立,消去\(D_{n-1}\),即得
\({D_n} = (\frac{1}{{a - b}})[b\prod\limits_{i = 1}^{n - 1} {({x_i} - a)} + a\prod\limits_{i = 1}^{n - 1} {({x_i} - b)} ]\)
第五类 三对角行列式
该行列式只有主对角线以及两条次对角线上的元素不为0.与双对角行列式类似,只是没有那个被挤出去的元素了
\({D_n}= \left| {\begin{array}{*{20}{c}} a&c&{}&{}&{}&{}\\ b&a&c&{}&{}&{}\\ {}&b&a&c&{}&{}\\ {}&{}& \cdots & \cdots & \cdots &{}\\ {}&{}&{}&b&a&c\\ {}&{}&{}&{}&b&a \end{array}} \right|\)
试试按第一列展开:肉眼可见\(a\)乘以它的代数余子式等于\(aD_{n-1}\).那么\(b\)的代数余子式呢?
\({A_{21}} = {( - 1)^{2 + 1}}b\left| {\begin{array}{*{20}{c}} c&{}&{}&{}&{}&{}\\ b&a&c&{}&{}&{}\\ {}&b&a&c&{}&{}\\ {}&{}&b&a&c&{}\\ {}&{}&{}& \cdots & \cdots & \cdots \\ {}&{}&{}&{}&b&a \end{array}} \right|\)
按第一行展开:\({A_{21}} = - bc{D_{n - 2}}\)
所以\({D_n} = a{D_{n - 1}} - bc{D_{n - 2}}\)
设\({D_n} - x{D_{n - 1}} = y({D_{n - 1}} - x{D_{n - 2}})\)
则可得到\(\left\{ {\begin{array}{*{20}{c}} {x + y = a}\\ {xy = bc} \end{array}} \right.\)
像不像韦达定理啊?我们据此构造一个一元二次方程\({t^2} - at + bc = 0\)
由于备考时间紧迫,下面的东西我实在不能深究,看不懂了,直接把结论贴上来吧:
\({D_n} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{y^{n + 1}} - {x^{n + 1}}}}{{y - x}}}&{,{a^2} - 4bc > 0}\\ {(n + 1){x^n}}&{{a^2} - 4bc = 0} \end{array}} \right.\)
(\(x\)、\(y\)是一元二次方程的两个实根)
第六类 Hessenberg型行列式
\({D_n} = \left| {\begin{array}{*{20}{c}} 1&2&3&4& \cdots &n\\ 1&{ - 1}&{}&{}&{}&{}\\ {}&2&{ - 2}&{}&{}&{}\\ {}&{}&3&{ - 3}&{}&{}\\ {}&{}&{}& \cdots & \cdots &{}\\ {}&{}&{}&{}&{n - 1}&{ - (n - 1)} \end{array}} \right|\)
上面这个就是Hessenberg型行列式.它的特点是除了第一行的其他行,有且仅有两个互为相反数的非零元素,且沿着主对角线和次对角线排列.
如果我们能把第二行的第一个元素消掉,那么我们就可以按照第一列展开,得到一个上三角行列式,直接进行计算.先试着用第一列加第二列.
\({D_n} = \left| {\begin{array}{*{20}{c}} {1 + 2}&2&3&4& \cdots &n\\ 0&{ - 1}&{}&{}&{}&{}\\ {0 + 2}&2&{ - 2}&{}&{}&{}\\ {}&{}&3&{ - 3}&{}&{}\\ {}&{}&{}& \cdots & \cdots &{}\\ {}&{}&{}&{}&{n - 1}&{ - (n - 1)} \end{array}} \right|\)
我们发现虽然第二行的第一个元素被消掉了,但是第三行第一个元素却不是0了.所以我们应该把第一列加上后面的所有列.
\({D_n} = \left| {\begin{array}{*{20}{c}} {1 + 2 + \cdots + n}&2&3&4& \cdots &n\\ 0&{ - 1}&{}&{}&{}&{}\\ 0&2&{ - 2}&{}&{}&{}\\ 0&{}&3&{ - 3}&{}&{}\\ \cdots &{}&{}& \cdots & \cdots &{}\\ 0&{}&{}&{}&{n - 1}&{ - (n - 1)} \end{array}} \right|\)
按第一列展开,直接得到\({D_n} = \frac{{n(n + 1)}}{2}{( - 1)^{n - 1}}(n - 1) = {( - 1)^{n - 1}}\frac{{(n + 1)!}}{2}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号