P4 矩阵的LU分解

https://www.bilibili.com/video/BV1zx411g7gq?p=4

https://www.bilibili.com/video/BV1Kt411y7jN?p=4

https://www.bilibili.com/video/BV1nb411t7Hg?p=4

http://bilibili.com/video/BV1AC4y187WN?p=4&spm_id_from=pageDriver

LU

L:low 下三角矩阵

U:up 上三角矩阵

首先证明上一讲遗留的一个公式：

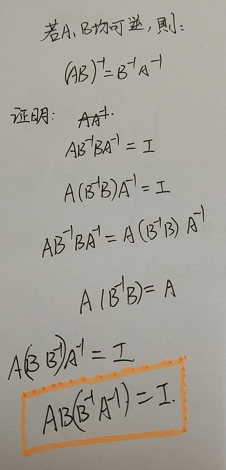
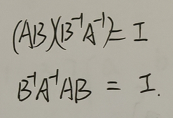
 括号可以拿掉。

 

转置和求逆，对于单个矩阵而言，顺序可以颠倒。

消元的目的是为了正确认识矩阵的概念。

 

 

 

 

 

 

 

对于三阶矩阵不需要换行进行消元的情况则有：

E₃₂(E₃₁(E₂₁A))=U，左乘逆矩阵可得   A=E₂₁-1E₃₁-1E₃₂-1U=LU

 

 

 

 E32(E31(E21A))=U的理解：

 

 

 

 

 

  E32E31E21A=U

结合律说括号可以去掉。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

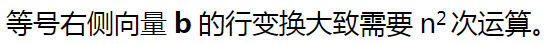
把第一列除了主元的元素都变为0，这样的运算做了100*99次运算。当第一行的k倍加到第2行的时候，每一列都要进行运算，总共有100列。第一行的k倍加到下面所有行，总共要加99次，每一次都有100个运算，所以第一阶段化简总共进行了100*99次运算。

第二阶段化简：99*98次运算，接近99²次运算。

.

.

.

第99阶段化简：2*1次运算，接近2²次运算。

n阶矩阵的LU分解总的运算次数大约是：1²+2²+3²+4²+...+(n-1)²+n²

 

矩阵的LU分解的一个目的是完成消元。