P3 矩阵乘法和逆矩阵

http://bilibili.com/video/BV1AC4y187WN?p=3&spm_id_from=pageDriver

要点：

1. 矩阵乘法。
2. 逆矩阵。

 

 

 

 

 

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

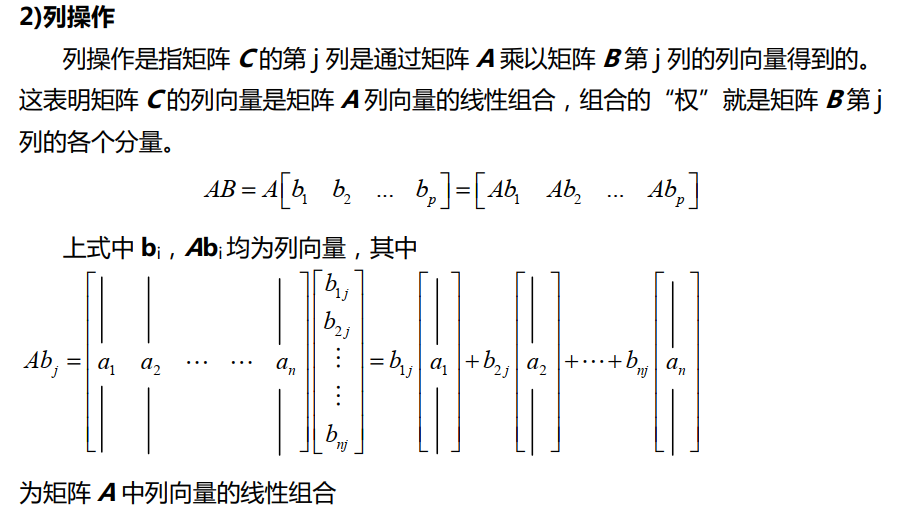
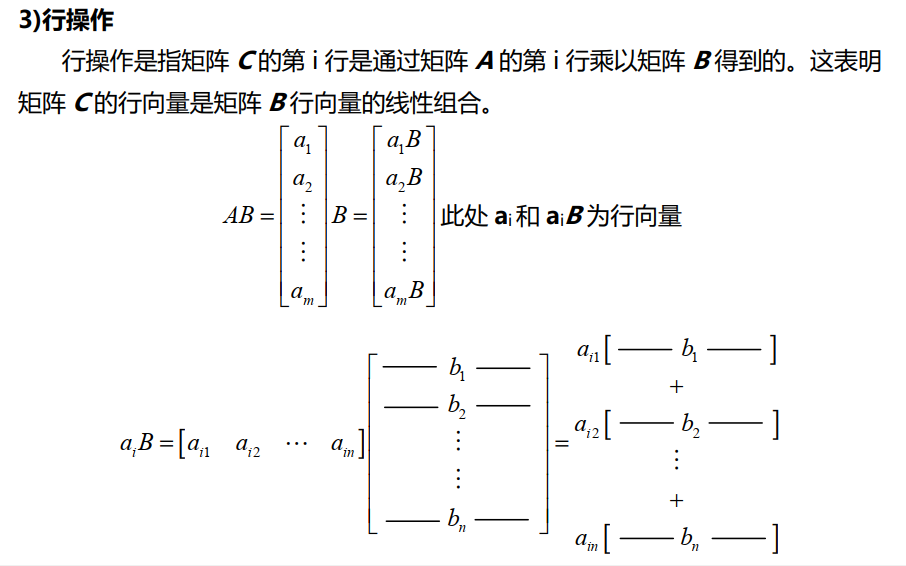
 矩阵乘法至此就讲清楚了。

 

 

 

 

 

 

 

 

 

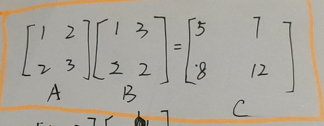
上一讲已经讲过，矩阵相乘，C的每一行相当于是B的行向量的线性组合。C的第一行是A的第一行的值作为权重对B的行向量进行的线性组合，C的第二行是A的第二行的值作为权重对B的行向量进行的线性组合。

 

 

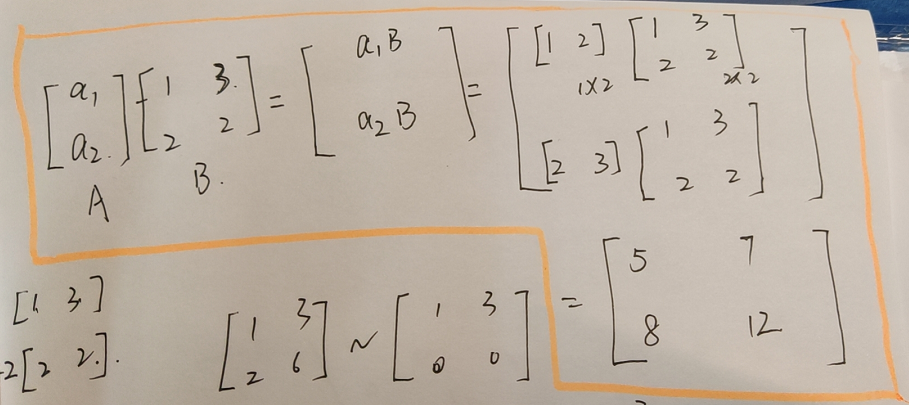
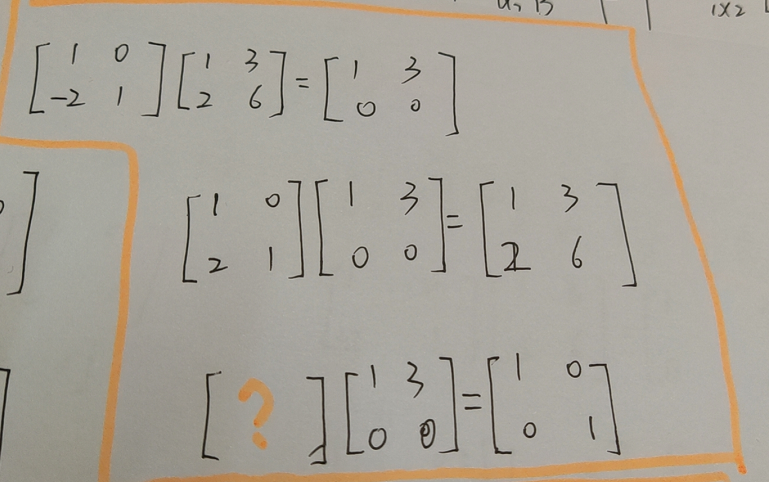
可逆矩阵就是一个矩阵经过一系列初等（行）变换后，可以变成单位阵的矩阵。但是这个矩阵在第二步的初等行变换的时候怎么也变不成单位阵，所以它不可逆。就是B矩阵无论什么样对C矩阵的行进行的线性组合都不会变成C矩阵的第一行[1 0].

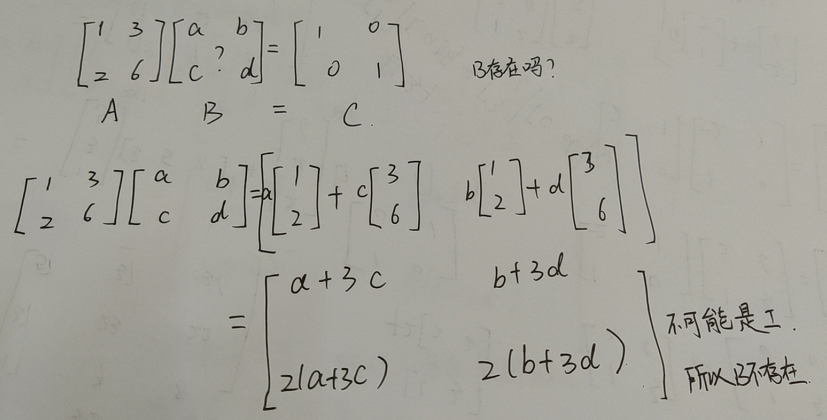
 A的两个列向量共线。

 

 

 

 

下面是可逆矩阵的求法。

 

 

 

 

 

 

 

 

 

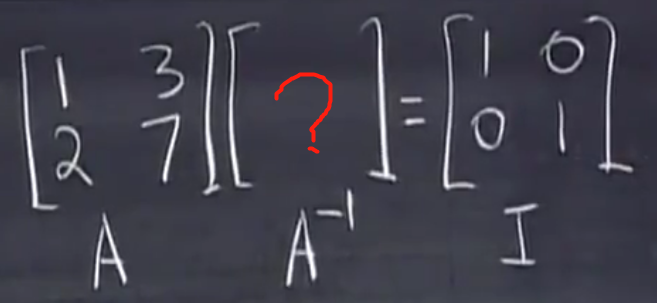
 这个是增广矩阵。

 

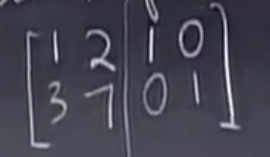
 增广矩阵。

 

 

 

 

系数矩阵在讲课的时候写错了。

 

 

 

 

 

 

 

 

 

 

 

这里的E是两个初等矩阵的乘积。