P13 向量组04

http://bilibili.com/video/BV1Gf4y1S7e5?p=13

 

 

 

 

注解：

1. 行列式，行和列处于同等的地位。
2. 高维向量可以表示低维向量，低维向量不能表示高维向量。
3. 被表示的维度低，主动表示的维度高。维度高的秩大，维度低的秩小。

 

 

 

 

 

 

 

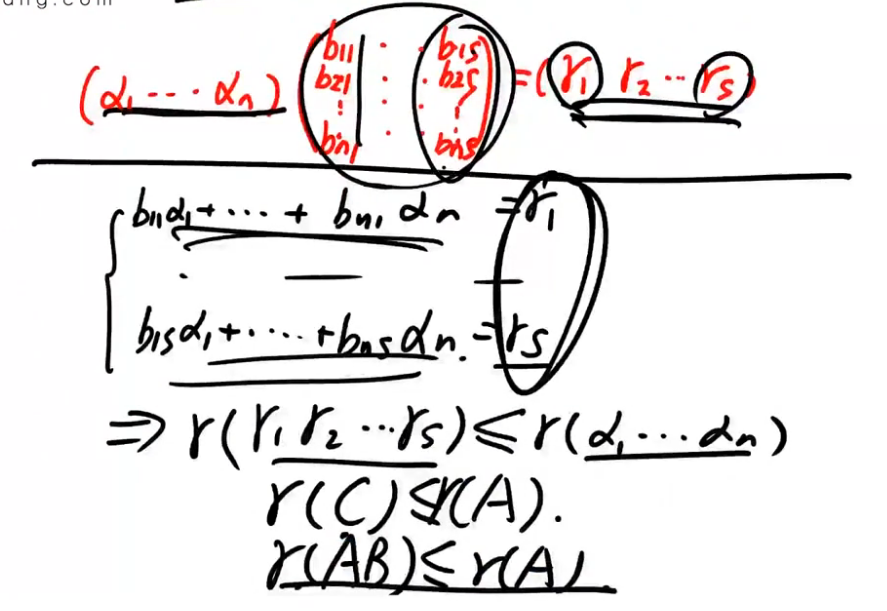
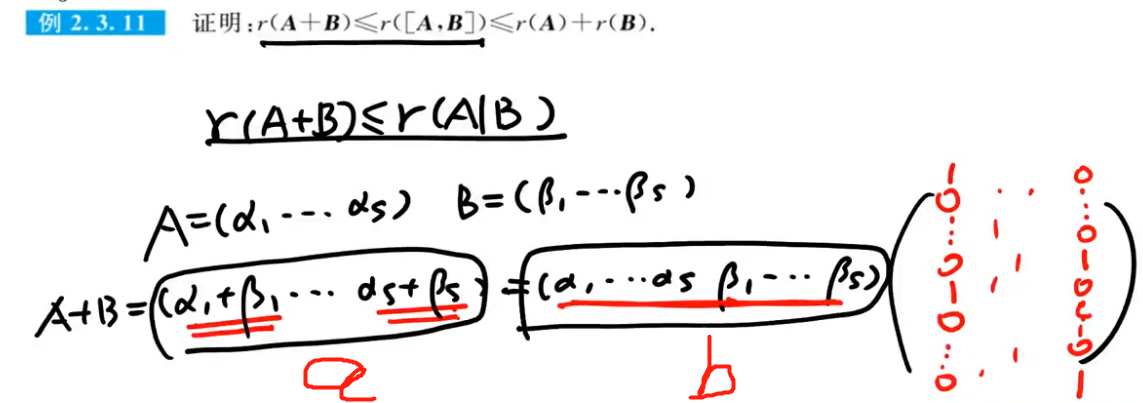
注解：

1. a向量组可以由b向量组表示，被表示的向量组秩大不，所以a向量组的秩小。

 

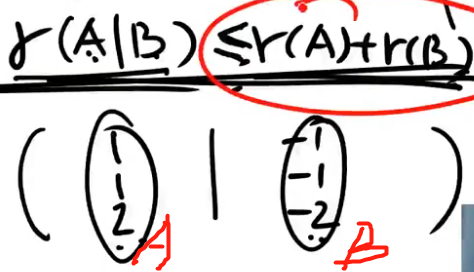
 注解:

1. A与B拼起来的秩少1.
2. 两个矩阵拼起来，秩可能会变小。

 

 

 

 

 

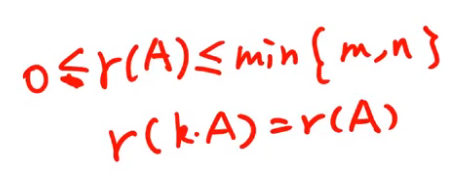
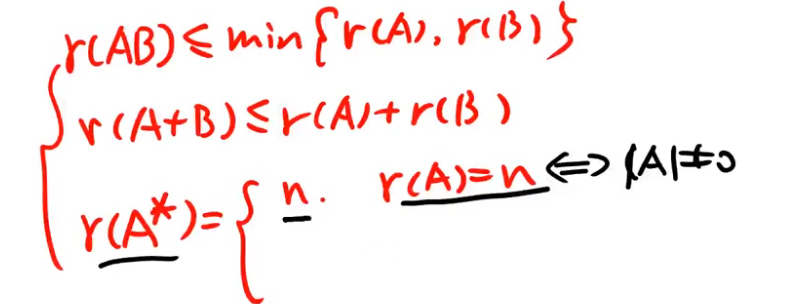
证明：

 

 

 

 

 

 

 

 

 

 

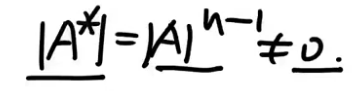
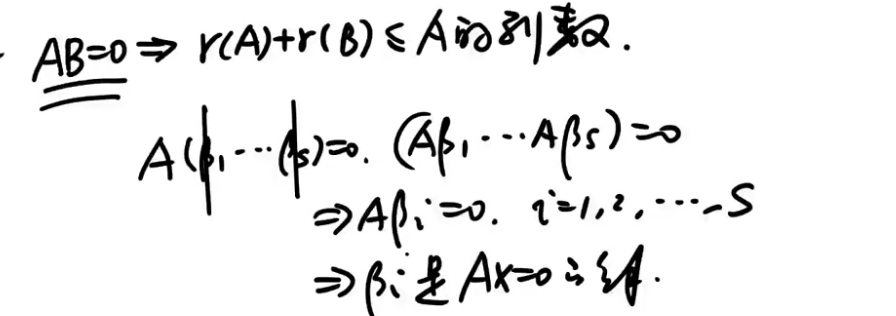
 注释：

1. 部分解可以被全部解表示，被表示的秩不大，所以r(B)≤n-r(A).

 

 

 

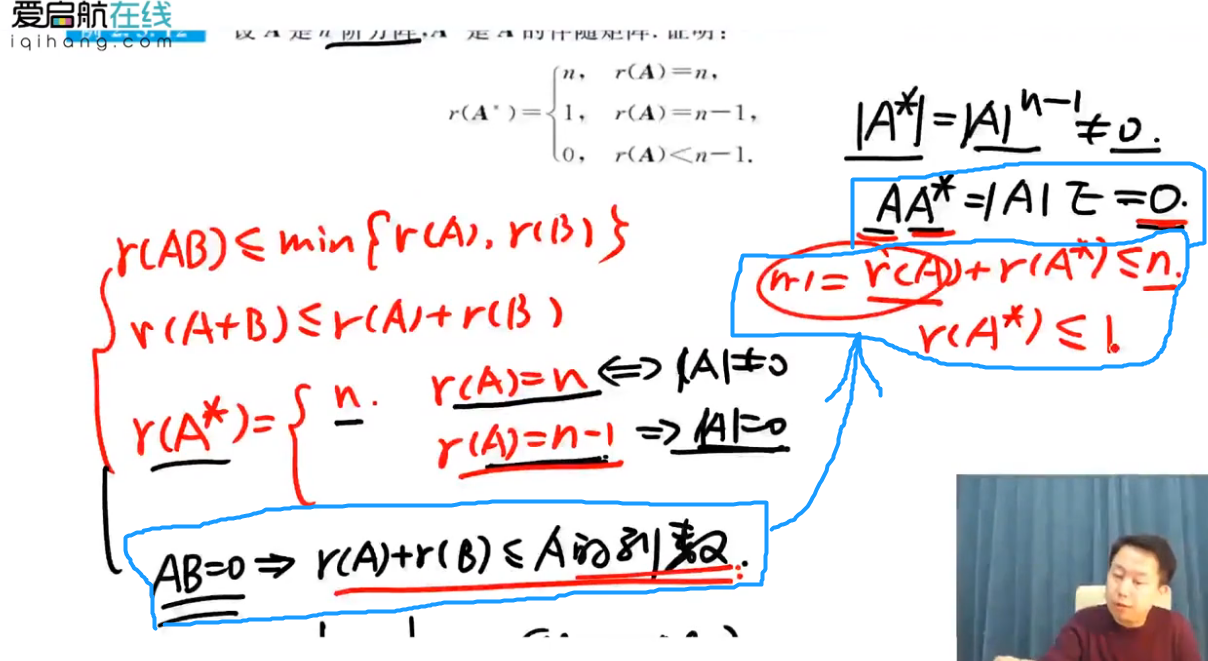
注解：

1. 意味着A中存在n-1阶行列式不是0.
2. 伴随阵是由代数余子式构成的，某元素的代数余子式是去掉它所在的行与列，剩余的n-1阶元素构成的，所以存在一个代数余子式不是0.所以伴随阵的秩至少是1.

 

 

---

 

 

 

 注解：

1. 秩小于n-1,就意味着任意n-1阶子式都是0.这意味着伴随矩阵的元素都是0元素，所以伴随矩阵的秩只能是0.

---

 

 

---

 

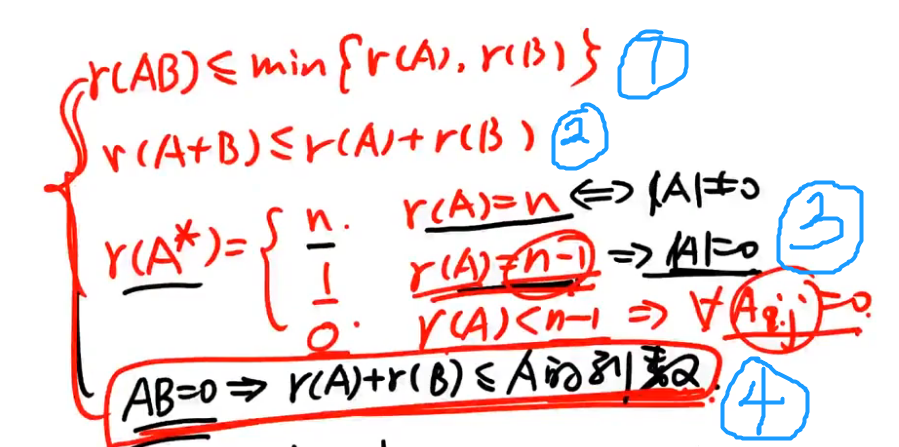
 注解：

1. 求矩阵的秩的时候，可以做初等行变换，也可以做初等列变换。

 

 

 

 

 

 

 

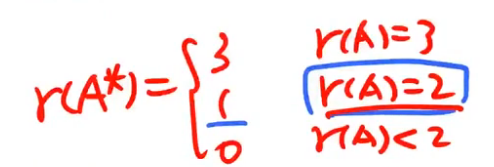
 注解：

1. 最后两列不成比例，立即得秩是2

---

 

 注解：

1. 3是A的列数。

 

 

 

---

 

 

 

 

---

 

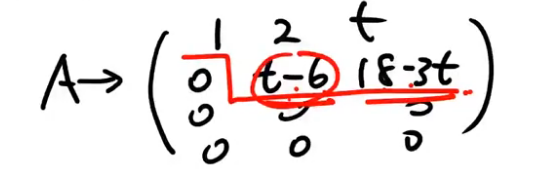
 注解：

1. 基不一定是正交的3个3维向量。
2. 线性无关的3个向量也可以是3维空间的一组基。
3. 基是有无数个的。

---

 

 

 

 

 

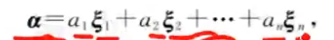
 注解：

1. 任意一个向量α不仅可以在一组正交基里面表示，也可以用任意一个基中表示。

 

---

 

 

---

 

 注解:

1. 定理9揭示了不同坐标系下的坐标变换公式。

---

 

                          

 

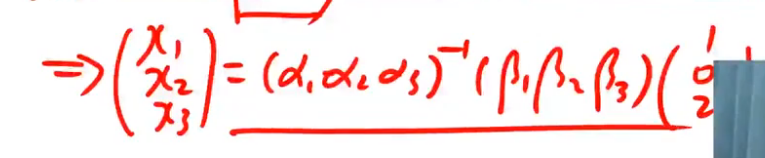
 第3讲完结!