相似变换和仿射变换

仿射变换的概念可以参考：3.1 相机标定的基本概念_哔哩哔哩_bilibili

1）平移变换

从一个位置到另一个位置的变换可以用平移矩阵T表示，该矩阵通过向量t=(t_x,t_y,t_z)对实体进行平移操作。

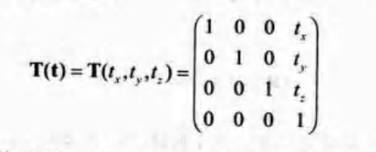其实还有另外一种形式（以左手坐标系为基准）：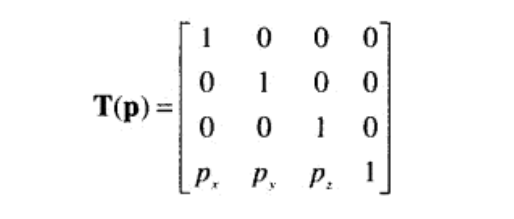

第一种形式（以右手坐标系为基准的）进行变换时将T与需要变换的点或向量A（列向量）相乘，即TA。第二种形式（以左手坐标系为基准）将需要变换的点或向量（行向量）与T相乘，即AT。

平移矩阵的逆矩阵为T^-1(t)= T(-t)，也就是对向量t进行了置负操作。

2）旋转变换

旋转矩阵 R_x(Θ)、R_y(Θ)、R_z(Θ)分别表示将物体绕x,y,z轴进行旋转。

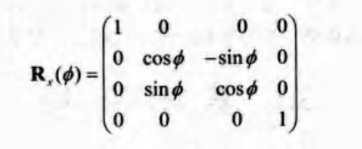
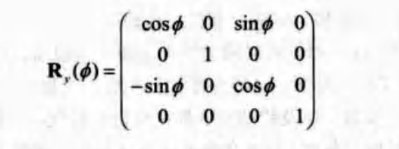
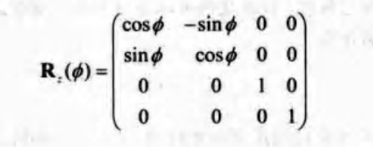
注意，旋转矩阵表示物体是绕着指定轴（轴的指向朝外面）按顺时针方向旋转的，但这个形式的旋转矩阵是以右手坐标系为基准的。

左手坐标系的为：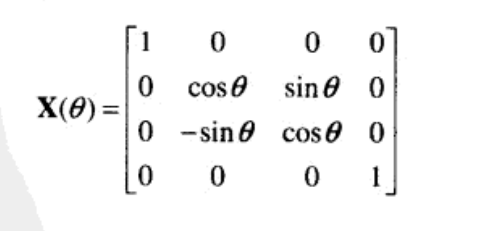

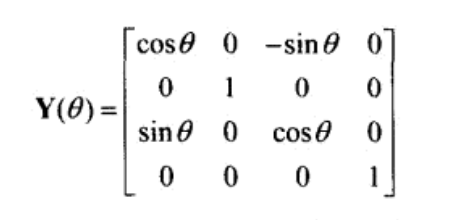
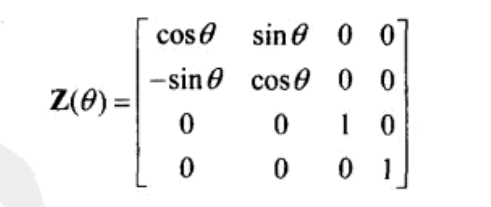
旋转矩阵的推导可以看这里：http://blog.csdn.net/zsq306650083/article/details/8773996

任意轴旋转任意角度矩阵：

对于这个3x3矩阵来说，其对角元素之和是一个与坐标轴无关的常数，称其为迹（Trace）：tr(R) = 1+2cosΘ

矩阵R的逆矩阵就是其转置矩阵，还有其他获取其逆矩阵的方法，即将Θ取负（绕着同一 坐标轴朝相反方向旋转）。旋转矩阵的行列式总是等于1.

3）缩放矩阵

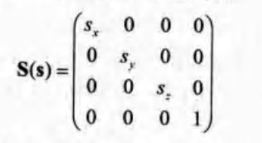    s_x,s_y,s_z分别表示沿着XYZ轴进行缩放的缩放比例。S矩阵的逆矩阵为S^-1(s) = S(1/s_x,1/s_y,1/s_z)。

如果对缩放矩阵s的一个或者三个分量置负，就会产生一个反射矩阵（镜像矩阵），如果其中两个缩放因子为-1，那么将旋转180度，当发现变换矩阵是反射矩阵时，需要进行特殊处理，例如，一个三角形的顶点序列以逆时针方向排列时，在经过反射矩阵变换后，对得到一个顺时针方向排列的三角形顶点序列，这将导致不正确的光照效果和背面裁减。判断给点矩阵是否为反射形式，需要计算该矩阵左上部3x3矩阵行列式的值，如果为负，那么该矩阵就为反射矩阵。

 

4）错切变换

错切矩阵有6种基本形式，分别表示为H_xy(s)、H_xz(s)、H_yx(s)、H_yz(s)、H_zx(s)、H_zy(s). 第一个下标表示由错切矩阵改变的坐标，第二个下标表示进行错切操作的坐标。

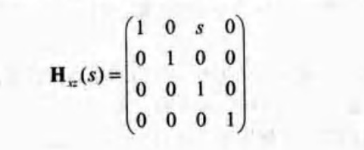  通过下标可以找到参数s所在的位置。如本例中x=0,z=2。

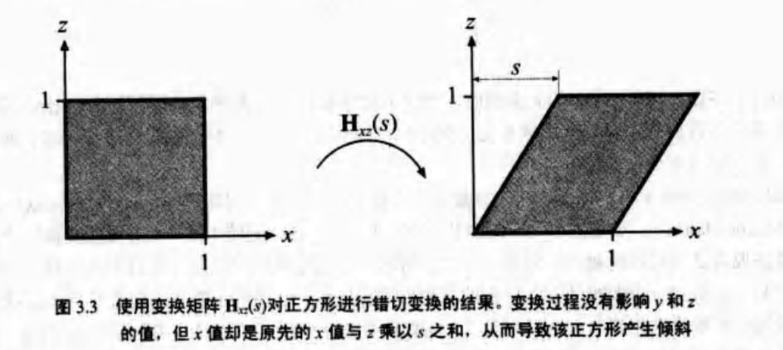    错切矩阵的逆矩阵可以通过取负来取得 (H_ij)^-1(s)= H_ij(-s)

5) 刚体变换

刚体变换用于刚性物体的变换，只改变物体的方向和位置，不改变形状。可以将刚体矩阵X写成一个平移矩阵和一个旋转矩阵的级联：

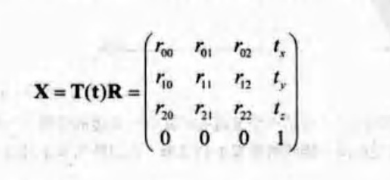
X的逆矩阵可以这样求得：X^-1=(T(t)R)^-1=R^-1T(t)^-1=R^TT(-t).

6)仿射变换

原理

对于二维坐标系的一个坐标点（x，y），可以使用一个2x2矩阵来调整x，y的值，而通过调整x，y可以实现二维形状的线性变换（旋转，缩放），所以整个转换过程就是对（x，y）调整的过程。

 

仿射变换（Affine Transformation）是指在向量空间中进行一次线性变换(乘以一个矩阵)和一次平移(加上一个向量)，变换到另一个向量空间的过程。

 

仿射变换代表的是两幅图之间的映射关系，仿射变换矩阵为2x3的矩阵，如下图中的矩阵M，其中的B起着 平移 的作用，而A中的对角线决定 缩放，反对角线决定 旋转 或 错切。

 

所以仿射变换可以由一个矩阵A和一个向量B给出：

 

原像素点坐标(x,y)，经过仿射变换后的点的坐标是T，则矩阵仿射变换基本算法原理：

 

所以仿射变换是一种二维坐标（x, y）到二维坐标（u, v）的线性变换，其数学表达式如下：

 

其实到这里还没完，我们知道缩放和旋转通过矩阵乘法来实现，而平移是通过矩阵加法来实现的，为了将这几个操作都通过一个矩阵来实现，所以构造出了上面那个 2x3 的矩阵。

 

但是这个会改变图像的尺寸，比如一个 2x2 的图像，乘以 2x3 的矩阵，会得到 2x3 的图像，所以为了解决这个问题，我们就增加一个维度，也就是构造齐次坐标矩阵。

 

关于齐次坐标的更多内容可以查看这里，还有这里。

 

最终得到的齐次坐标矩阵表示形式为：

 

仿射变换保持了二维图像的“平直性”和“平行性”：

平直性：

• 直线经仿射变换后还是直线
• 圆弧经仿射变换后还是圆弧

平行性：

• 直线之间的相对位置关系保持不变
• 平行线经仿射变换后依然为平行线
• 直线上点的位置顺序不会发生变化
• 向量间夹角可能会发生变化

7) 法线变换

注意，法线必须通过用变换几何图形的矩阵的逆矩阵的转置矩阵进行变换 N=(M^-1)^T

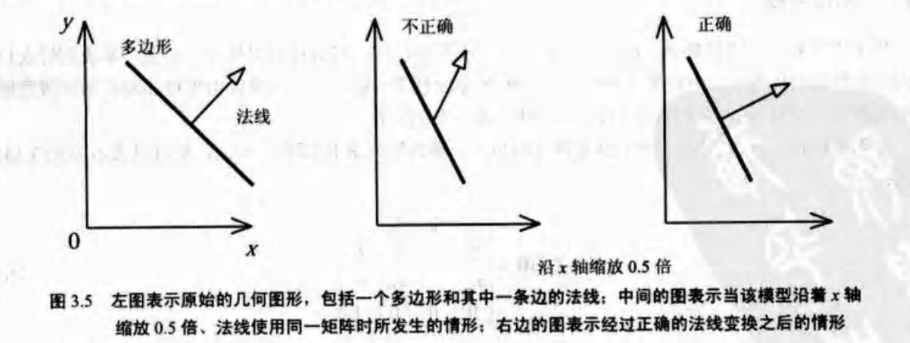
实际应用中，如果变换矩阵是正交的（如旋转矩阵），就没必要计算它的逆矩阵，因为正交矩阵的逆矩阵就是转置矩阵，两个转置矩阵相互抵消，相乘的结果还是原来的旋转矩阵。此外，还有平移矩阵，由于平移不改变向量的方向，所以可以进行任意次数的平移而不对法线产生任何影响。另外，如果使用一个或多个一致性缩放矩阵进行变换，也不需要计算相应的逆矩阵，因为这种缩放只改变法线长度，不影响其方向。这种矩阵进行变换之后需要对法线进行归一化（规范化）。

来源：https://www.cnblogs.com/ll-10/p/5470637.html