P1350 车的放置 题解

一、题目描述：

　　给你一个网格棋盘，$a,b,c,d$ 表示了对应边长度，也就是对应格子数。

　　例如，当 $a=b=c=d=2$ 时，对应了下面这样一个棋盘：

　　　　　　　　　　

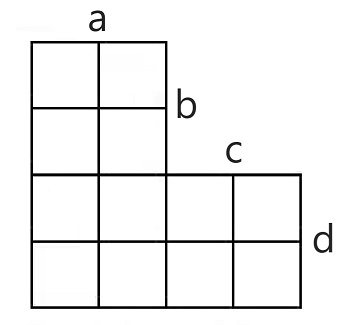
　　想要在这个棋盘上放 k 棋子，也就是这 k 个棋子没有两个在同一行，也没有两个在同一列，问有多少种方案。

　　答案对 $1e5+3$ 取模。数据保证 $0<=a,b,c,d,k<=1e3$，且至少有一种可行方案。

---

二、解题思路：

　　棋子是一行一行、一列一列的攻击的，所以我们可以一列一列的 $dp$ 。

　　设 $f_{i,j}$ 表示前 $i$ 列放 $j$ 个棋子的方案数，$s_i$ 表示第 $i$ 列的方格数。

　　容易得到状态转移方程：$f_{i,j}=f_{i-1,j}+f_{i-1,j-1}\times (s_i-(j-1))$。

 

　　其实很好理解：

　　第 i 列不放棋子的情况下，$f_{i,j}+=f_{i-1,j}$。这种情况不用说了吧？

　　第 i 列要放棋子的情况下，$f_{i,j}+=f_{i-1,j-1}\times$第 $i$ 列剩余位置数量。

　　

　　关于 第 i 列剩余位置数量：

　　一列一列地来看，我们 $dp$ 方程一列本来就最多放一个，不用管。

　　一行一行地来看，$f_{i-1,j-1}$ 表示前 $i-1$ 行放了 $j-1$ 个棋子。

　　一个棋子占据一行，其实就是第 $i$ 列有 $j-1$ 行不能放了。

　　那么还剩下 $s_i-(j-1)$ 个位置，$f_{i,j}+=f_{i-1,j-1}\times (s_i-(j-1))$。

 

　　但其实还有一个问题（困扰了我很久）：

　　如果 $i-1$ 列有一些行是第 $i$ 列没有的怎么办？例如最上面的图。

　　转移从左往右数的第 $3$ 列时，第 $2$ 列的方案里有一些是棋子放在了上面两行。

　　这些棋子显然不会占据第 $3$ 列的空位，但状态转移方程会 默认占用第 $3$ 列的空位，导致方案数减少。

　　

　　怎么解决呢？

　　显然只有 $s_{i-1}>s_i$ 才会出现这种问题，所以从右往左倒着转移就好了！

 

　　时间复杂度 $O((a+c)k)$，可以通过，而且很快。

---

三、完整代码：

#include<iostream>
#define N 2010
using namespace std;
int a,b,c,d,k;
int s[N],f[N][N];
int main()
{
    cin>>a>>b>>c>>d>>k;
    for(int i=1;i<=a;i++)    s[i+c]+=b;
    for(int i=0;i<=a+c;i++)    s[i]+=d+1,f[i][0]=1;
    for(int i=1;i<=a+c;i++)
        for(int j=1;j<=k;j++)
            f[i][j]=(f[i-1][j-1]*(s[i]-j)+f[i-1][j])%M;
    cout<<f[a+c][k]<<'\n';
    return 0;
}

---

四、写题心得：

　　好了，总算把这题想明白了，状态转移方程也是自己推的。很好，加油！