CF1818D 题解

一、题目描述：

　　给你一颗 $n$ 个点，$m$ 条边的简单无向图，可能不连通。

　　我们定义 $鱼图$ 为满足以下条件的无向图：

　　　　$包含恰好\ 1\ 个环，环上有\ 1\ 个特殊的结点\ u\ ，u\ 除了连在环上的\ 2\ 条边外还正好有\ 2\ 条边连向不在此环上的结点。$

　　求是否存 $鱼图$。若存在，输出 $YES$ 和这个鱼图。若不存在，输出 $NO$。数据范围 $1\leq n,m\leq 2\times 10^3$。

二、解题思路：

　　我们考虑找到上述 $特殊的节点$ 。

　　发现这个节点只要在环中，并且只要有 $4$ 条边就行了。

　　边数好判断，怎么判断一个点是否在环中呢？

　　$sb-yhy$ 告诉我们，可以用拓扑排序判环。

　　是的，我们确实可以用拓扑排序判环，于是我就寄了。

　　给大家看这样一个图：

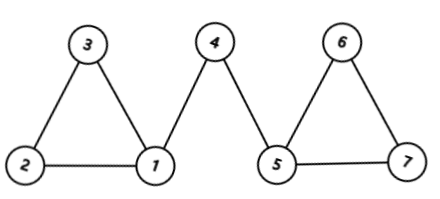
　　这个神奇的 $4$ 号节点其实不在环上，但是却不会被判出来。

　　所以，可以使用拓扑排序判断是否有环，但不能使用拓扑排序判断一个点是否在环上。

　　那该如何判断呢？考虑 $dfs$ 找环，于是我就又寄了。

　　给大家看这样一个图：

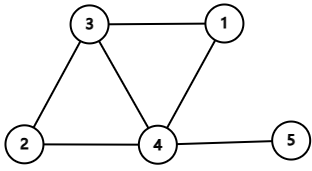
　　在这个图中，如果我们找到的环是 $4-1-3-2-4$，你就会发现 $4$ 号节点只剩下一条边没有连在环上，满足不了 $鱼图$ 的条件了。

　　所以我们要找最小环。于是请 $bfs$ 登场。

　　记录下前驱，如果搜到已经搜过的点，那么环就找到了，于是我又寄了。

　　回到最上面那个图：

　　我们会搜索到 $2$ 号和 $3$ 号节点相连，但 $4$ 号节点仍然不在环中。

　　所以我 $很聪明的$ 去看了题解，得到了 $Alex\_wei$ 的启发：

　　　　$记录下每个节点是从原点的哪一个邻接点出来的，记为\ top_i。如果\ top_i\ 不一样，则找到了环。$

　　于是我终于 $顺利$ 地过掉了这个题。时间复杂度 $O(n \times m)$。

三、完整代码：

 1 #include<iostream>
 2 #define N 2010
 3 #define to edge[i].v
 4 using namespace std;
 5 int T,n,m,x,u1,v1,cc,l,r;
 6 int h[N],q[N],f[N],d[N],du[N],tp[N],vis[N],pre[N];
 7 struct EDGE{
 8     int v,nxt;
 9 }edge[N*2];
10 int head[N],cnt;
11 void add(int u,int v)
12 {
13     edge[++cnt].v=v;
14     edge[cnt].nxt=head[u];
15     head[u]=cnt;
16 }
17 void print(int s,int u,int v)
18 {
19     for(int i=1;i<=n;i++)f[i]=0;
20     x=u;while(x!=s)f[x]=1,x=pre[x],cc++;
21     x=v;while(x!=s)f[x]=1,x=pre[x],cc++;
22     cout<<"Yes"<<'\n'<<cc<<'\n';
23     x=u;while(x!=s)
24         cout<<x<<" "<<pre[x]<<'\n',x=pre[x],cc--;
25     x=v;while(x!=s)
26         cout<<x<<" "<<pre[x]<<'\n',x=pre[x],cc--;
27     cout<<u<<" "<<v<<'\n',cc--;
28     for(int i=head[s];i!=-1;i=edge[i].nxt)
29         if(!f[to]&&cc)    cout<<s<<" "<<to<<'\n',cc--;
30 }
31 int Try(int u)
32 {
33     l=r=0;
34     for(int i=1;i<=n;i++)    f[i]=0;
35     for(int i=head[u];i!=-1;i=edge[i].nxt)
36         q[++r]=to,pre[to]=u,f[to]=1,tp[to]=to;
37     while(l<r)
38     {
39         int x=q[++l];
40         for(int i=head[x];i!=-1;i=edge[i].nxt)
41             if(pre[x]!=to&&!vis[x])
42             {
43                 if(!f[to])q[++r]=to,f[to]=1,pre[to]=x,tp[to]=tp[x];
44                 else if(tp[x]!=tp[to]) {print(u,x,to);return 1;}
45             }
46     }
47     return 0;
48 }
49 void top_sort()
50 {
51     l=r=0;
52     for(int i=1;i<=n;i++)
53         d[i]=du[i];
54     for(int i=1;i<=n;i++)
55         if(du[i]==1)
56             q[++r]=i,vis[i]=1;
57     while(l<r)
58     {
59         int u=q[++l];
60         for(int i=head[u];i!=-1;i=edge[i].nxt)
61         {
62             du[to]--;
63             if(!vis[to]&&du[to]<2)
64                 q[++r]=to,vis[to]=1;
65         }
66     }
67     for(int i=1;i<=n;i++)
68         du[i]=d[i];
69 }
70 void solve()
71 {
72     cin>>n>>m;cnt=0;cc=3;
73     for(int i=1;i<=n;i++)
74         head[i]=-1,f[i]=du[i]=vis[i]=0;
75     for(int i=1;i<=m;i++)
76     {
77         cin>>u1>>v1;
78         add(u1,v1),du[u1]++;
79         add(v1,u1),du[v1]++;
80     }
81     top_sort();
82     for(int i=1;i<=n;i++)
83         if(du[i]>=4&&!vis[i])
84             if(Try(i))    return ;
85     cout<<"NO"<<'\n';
86 }
87 int main()
88 {
89     ios::sync_with_stdio(false);
90     cin.tie(0);cout.tie(0);
91     cin>>T;
92     for(int i=1;i<=T;i++)
93         solve();
94     return 0;
95 }

四、写题心得：

　　原来我的图论板块还有这么多漏洞，还得好好学啊。加油！拜拜！

posted on 2023-06-05 09:11 trh0630 阅读(53) 评论(0) 收藏举报