常见Hilber变换对 各种摘抄

目录

• 熟记一个fourier变换对
• 希尔伯特变换定义
• Hilbert变换对图片
• mma计算希尔伯特变换
• 参考

熟记一个fourier变换对

如果傅里叶变换采用最常见的那种记法 \(\int f(t)e^{-j\Omega}t dt\),那么

\[\frac{1}{\pi t}\leftrightarrow -j \ \text{sgn}(\Omega) \]

用到了如下积分：

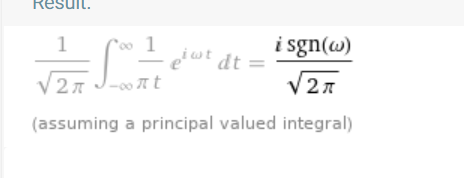
希尔伯特变换定义

\[\boldsymbol{H}\{f( t)\}:=f(t)*\frac{1}{\pi t} \]

Hilbert变换对图片

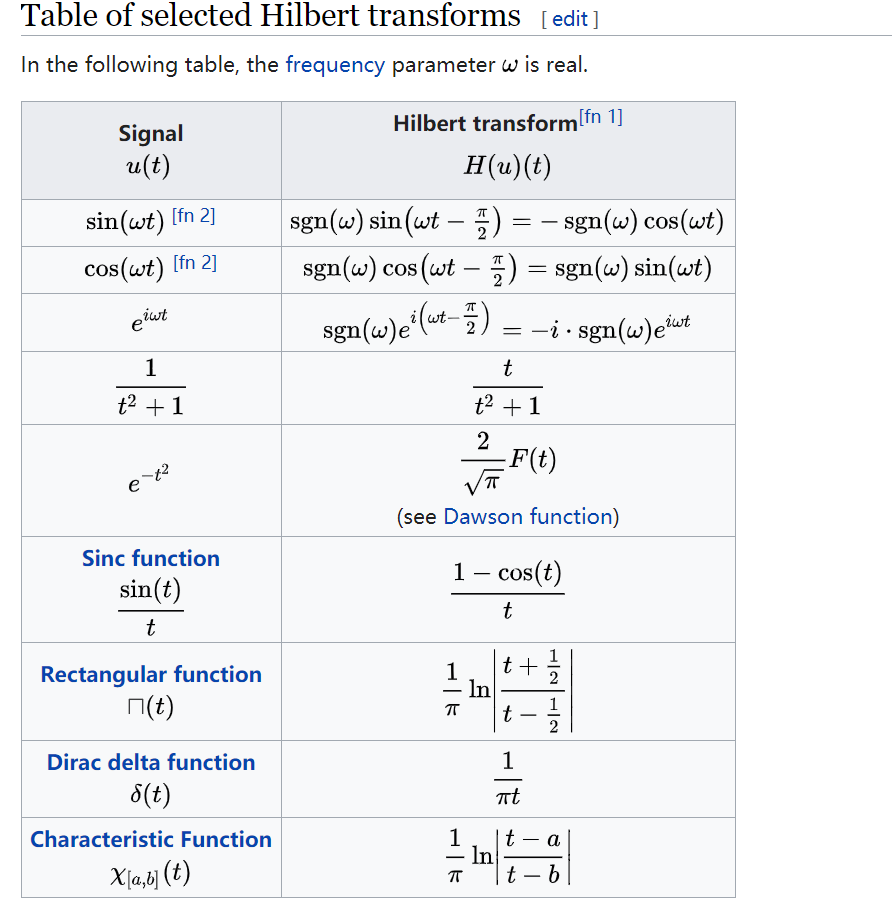
mma计算希尔伯特变换

(*去stackExchange里翻到了mma版本的*)
hilbertTransform[f_, u_, t_] := 
 FullSimplify[Convolve[f, 1/u, u, t, PrincipalValue -> True]/\[Pi]]

hilbertTransform[Sin[v], v, t]

hilbertTransform[Cos[v], v, t]

参考

https://mathematica.stackexchange.com/questions/341/implementing-discrete-and-continuous-hilbert-transforms