01背包

 有n件物品，每件物品的重量为w[i]，价值为c[i]。现有一个容量为V的背包，问如何选取物品放入背包，使得背包内物品的总价值最大。其中
每种物品都只有一件。

令dp[i][j]来表示前i件物品装入容量为j的背包所能得到的最大总价值。

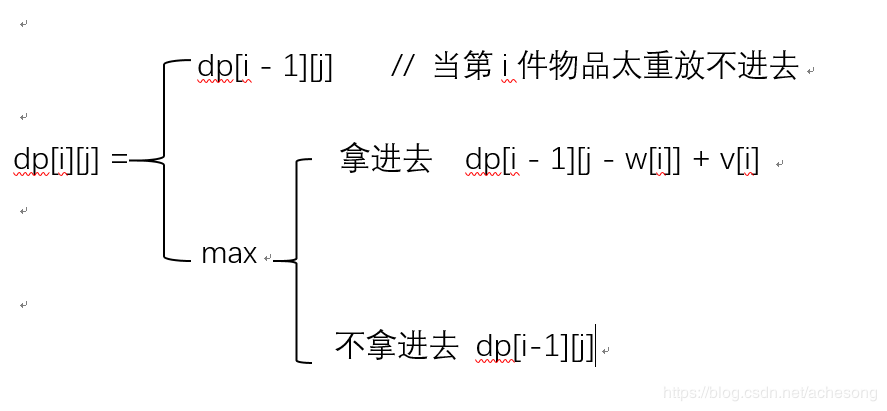
对于dp[i][j]来说，i指的是前i件物品，j指的是还剩下多少背包空间。于是对于dp[i][j]来说，有公式

编号i	重量w[i]	价格v[i]	背包容量 W = 20
1	2	3
2	3	4
3	4	5
4	5	8
5	9	10

 

表格（即这个过程本质是填写下面的这个表格）：

capacity=>	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
no items	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
w=2   v=3	0	0	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
w=3   v=4	0	0	3	4	4	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7
w=4   v=5	0	0	3	4	5	7	8	9	9	12	12	12	12	12	12	12	12	12	12	12	12
w=5   v=8	0	0	3	4	5	8	8	11	12	13	15	16	17	17	20	20	20	20	20	20	20
w=9   v=10	0	0	3	4	5	8	8	11	12	13	15	16	17	17	20	20	21	22	23	25	26

表格标红的地方就是我们要求的dp[5][20]
接下来对表格每个位置进行说明，那第一行来说，表示的是前0件物品，背包容量为0~20时可以放进去的最大价值，物品都没有，不管容量多大可以容纳的价值都是0；
同样的，比如第二行，表示前1件物品（此物品重量为2，价值为3）在背包剩余容量为0时，放不下去，此时最大价值是0；背包剩余容量是1时，放不下去，此时最大价值是0；背包剩余容量为2时，能放进去，此时最大价值是3···
那么到了第3行（前2件物品），在背包容量是5的时候，为了达到最大价值，可以把第1件和第2件商品都放进去，5 >= 2 + 3，可以放下，最大价值为3 + 4 = 7。
整个表格的填写由程序来完成，计算公式为上面所列出的dp[i][j]计算公式。最后只需要取出我们所需要的dp[5][20]即可得到前5件物品，背包容量为20时的最大价值。
下面是程序：

#include <stdio.h>
#include<algorithm> 
#define N 6
#define M 21
#define W 20
using namespace std;
int dp[N][M];
int w[N] = {0};
int v[N] = {0};
void knapsack(){
    int i, j;
    int value1, value2;
    for(i = 1; i < N; i++){    // 前i件物品
        for(j = 1; j < N; j++){    // 背包剩余空间
            if(w[i] > j){    // 第i件物品太重放不进去
                dp[i][j] = dp[i - 1][j];
            }    
            else{
                value1 = dp[i-1][j - w[i]] + v[i];    // 第i件物品放进去
                value2 = dp[i-1][j];    // 第i件物品不放进去
                dp[i][j] = max(value1, value2);
            }
        }    
    }
}
int main(){
    knapsack();
    printf("%d\n", dp[5][20]);        // 5件物品，背包容量为20，最多可以放的价值
    return 0;
}