Python-插入排序

1、直接插入排序流程图

插入排序：每一趟都要把待排序数放到有序区中合适的插入位置

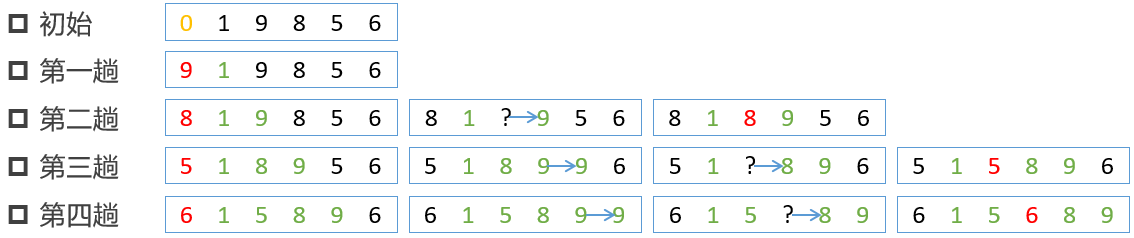
2、核心算法

结果可为升序或降序排列，默认升序排列。以升序为例
扩大有序区，减小无序区。图中绿色部分就是增大的有序区，黑色部分就是减小的无序区
增加一个哨兵位，图中最左端红色数字，其中放置每一趟待比较数值
将哨兵位数值与有序区数值从右到左依次比较，找到哨兵位数值合适的插入点

3、算法实现

3.1、增加哨兵位

为了方便，采用列表头部索引0位置插入哨兵位
每一次从有序区最右端后的下一个数，即无序区最左端的数放到哨兵位

3.2、比较与挪动

从有序区最右端开始，从右至左依次与哨兵比较
比较数比哨兵大，则右移一下，换下一个左边的比较数
直到找到不大于哨兵的比较数，这是把哨兵插入到这个数右侧的空位即可

3.3、代码示例

m_list = [
    [1, 9, 8, 5, 6, 7, 4, 3, 2],
    [1, 2, 3, 4, 5, 6, 7, 8, 9],
    [9, 8, 7, 6, 5, 4, 3, 2, 1]
]
nums = [0] + m_list[0]
print(nums[1:])
length = len(nums)
count_move = 0
for i in range(2, length):  # 测试的值从nums的索引2开始向后直到最后一个元素
    nums[0] = nums[i]  # 索引0位哨兵，索引1位假设的有序区，都跳过
    j = i - 1  # i左边的那个数就是有序区末尾
    if nums[j] > nums[0]:  # 如果最右侧数大于哨兵才需要挪动和插入
        while nums[j] > nums[0]:
            nums[j + 1] = nums[j]  # 右移，不是交换
            j -= 1  # 继续向左
            count_move += 1
            nums[j + 1] = nums[0]  # 循环中多减了一次j
print(nums[1:])

4、总结

最好情况，正好是升序排列，比较迭代n-1次
最差情况，正好是降序排列，比较迭代1,2,...,n-1即 n(n-1)/2，数据移动非常多
使用两层嵌套循环，时间复杂度O(n^2)

稳定排序算法
如果待排序序列R中两元素相等，即Ri等于Rj，且i < j ，那么排序后这个先后顺序不变，这种
排序算法就称为稳定排序

使用在小规模数据比较

优化
如果比较操作耗时大的话，可以采用二分查找来提高效率，即二分查找插入排序

5、排序稳定性

冒泡排序，相同数据不交换，稳定
直接选择排序，相同数据前面的先选择到，排到有序区，不稳定
直接插入排序，相同数据不移动，相对位置不变，稳定