1、简介
1.1、作用
集合,简称集。由任意个元素构成的集体。高级语言都实现了这个非常重要的数据结构类型。
Python中,它是可变的、无序的、不重复的元素的集合。
1.2、元素性质
去重:在集合中,所有元素必须相异
无序:因为无序,所以不可索引
可哈希:Python集合中的元素必须可以hash,即元素都可以使用内建函数hash
目前学过不可hash的类型有:list、set、bytearray
可迭代:set中虽然元素不一样,但元素都可以迭代出来
2、初始化
2.1、语法
set() -> new empty set object
set(iterable) -> new set object
2.2、示例
s1 = set()
s2 = set(range(5))
s3 = set([1, 2, 3])
s4 = set('abcdabcd')
s5 = {} # <class 'dict'>
s6 = {1, 2, 3} # <class 'set'>
s7 = {1, (1,)} # <class 'set'>
# s8 = {1, (1,), [1]} # 报错:list不可hash
3、增加
3.1、语法
add(elem)
增加一个元素到set中
如果元素存在,什么都不做
update(*others)
合并其他元素到set集合中来
参数others必须是可迭代对象就地修改
3.2、示例
s = set()
s.add(1)
s.update((1,2,3), [2,3,4])
print(s) # {1, 2, 3, 4}
4、删除
4.1、语法
remove(elem)
从set中移除一个元素
元素不存在,抛出KeyError异常。为什么是KeyError?
discard(elem)
从set中移除一个元素
元素不存在,什么都不做
pop() -> item
移除并返回任意的元素。为什么是任意元素?
空集返回KeyError异常
clear()
移除所有元素
4.2、示例
s = set(range(10))
s.remove(0)
# s.remove(11) # KeyError为什么,越界
s.discard(11)
s.pop()
s.clear()
5、修改、索引、遍历
5.1、修改
集合类型没有修改。因为元素唯一。如果元素能够加入到集合中,说明它和别的元素不一样。
所谓修改,其实就是把当前元素改成一个完全不同的元素,就是删除加入新元素。
5.2、索引
5.3、遍历
6、成员运算符in
6.1、IPython魔术方法
6.1.1、in方法
print(10 in [1, 2, 3])
print(10 in {1, 2, 3})
# 上面2句代码,分别在列表和集合中搜索元素。如果列表和集合的元素都有100万个,谁的效率高?
6.1.2、IPython内置的特殊方法,使用%百分号开头
% 开头是line magic
%% 开头是 cell magic,notebook的cell
6.1.3、语法
%timeit statement
-n 一个循环loop执行语句多少次
-r 循环执行多少次loop,取最好的结果
%%timeit setup_code
* code.....
# 下面写一行,列表每次都要创建,这样写不好
%timeit (-1 in list(range(100)))
# 下面写在一个cell中,写在setup中,列表创建一次
%%timeit l=list(range(1000000))
-1 in l
6.2、set和list in运算符性能比较
6.2.1、list
%%timeit list1=list(range(100))
a = -1 in list1
# 743 ns ± 6.16 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
%%timeit list2=list(range(1000000))
a = -1 in list2
# 7.58 ms ± 48.6 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
6.2.2、set
%%timeit set1=set(range(100))
a = -1 in set1
# 19 ns ± 0.173 ns per loop (mean ± std. dev. of 7 runs, 100,000,000 loops each)
%%timeit set2=set(range(1000000))
a = -1 in set2
# 18.8 ns ± 0.112 ns per loop (mean ± std. dev. of 7 runs, 100,000,000 loops each)
6.2.3、集合性能很好,为什么?
线性数据结构,搜索元素的时间复杂度是O(n),即随着数据规模增加耗时增大
set、dict使用hash表实现,内部使用hash值作为key,时间复杂度为O(1),查询时间和数据规模无关,不会随着数据规模增大而搜索性能下降。
7、可哈希
数值型int、float、complex
布尔型True、False
字符串string、bytes
tuple
None
以上都是不可变类型,称为可哈希类型,hashable set元素必须是可hash的。
8、集合概念
8.1、简介
全集 :所有元素的集合。例如:实数集,所有实数组成的集合就是全集
子集subset和超集superset
一个集合A所有元素都在另一个集合B内,A是B的子集,B是A的超集
真子集和真超集: A是B的子集,且A不等于B,A就是B的真子集,B是A的真超集
并集:多个集合合并的结果
交集:多个集合的公共部分
差集:集合中除去和其他集合公共部分
8.2、并集
8.2.1、原理图
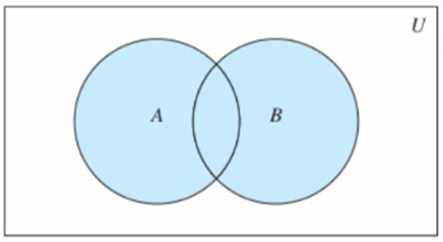
8.2.2、语法说明
将两个集合A和B的所有的元素合并到一起,组成的集合称作集合A与集合B的并集
union(*others) 返回和多个集合合并后的新的集合
| 运算符重载,等同union
update(*others) 和多个集合合并,就地修改
|= 等同update
8.3、交集
8.3.1、原理图
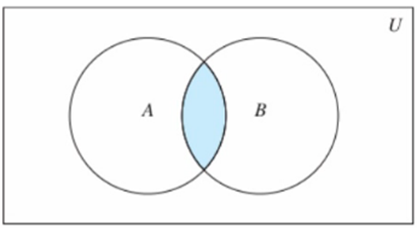
8.3.2、语法说明
集合A和B,由所有属于A且属于B的元素组成的集合
intersection(*others) 返回和多个集合的交集
& 等同intersection
intersection_update(*others) 获取和多个集合的交集,并就地修改
&= 等同intersection_update
8.4、差集
8.4.1、原理图
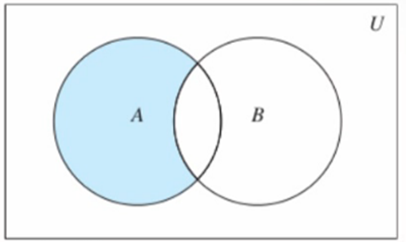
8.4.2、语法说明
集合A和B,由所有属于A且不属于B的元素组成的集合
difference(*others) 返回和多个集合的差集
- 等同difference
difference_update(*others) 获取和多个集合的差集并就地修改
-= 等同difference_update
8.5、对称差集
8.5.1、原理图
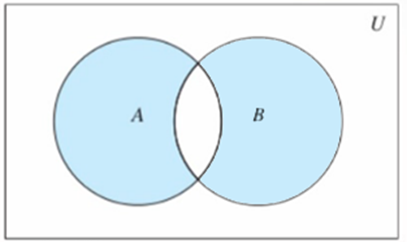
8.5.2、语法说明
集合A和B,由所有不属于A和B的交集元素组成的集合,记作(A-B)∪(B-A)
symmetric_differece(other) 返回和另一个集合的对称差集
^ 等同symmetric_differece
symmetric_differece_update(other) 获取和另一个集合的对称差集并就地修改
^= 等同symmetric_differece_update
8.6、其它集合运算
issubset(other)、<= 判断当前集合是否是另一个集合的子集
set1 < set2 判断set1是否是set2的真子集
issuperset(other)、>= 判断当前集合是否是other的超集
set1 > set2 判断set1是否是set2的真超集
isdisjoint(other) 当前集合和另一个集合没有交集,没有交集,返回True
9、集合使用案例
9.1、需求
一个总任务列表,存储所有任务。一个已完成的任务列表。找出为未完成的任务
9.2、实现过程
业务中,任务ID一般不可以重复
所有任务ID放到一个set中,假设为ALL
所有已完成的任务ID放到一个set中,假设为COMPLETED,它是ALL的子集
ALL - COMPLETED => UNCOMPLETED






 浙公网安备 33010602011771号
浙公网安备 33010602011771号