数据结构(一) - 教程
大纲
1. 数据结构、算法
2. 线性表:顺序表、链表、栈、队列
3. 树:性质、遍历方法、二叉树
4. 查询方法、排序方式
1.为什么要学习数据结构?
C语言告诉大家如何写程序,数据结构是告诉大家如何简洁高效的写程序。
2.遇到一个实际问题,需要写程序来实现相应的功能,需要解决哪两个方面的问题?
1) 如何表达数据元素之间的逻辑规律,以及如何将数据存储到计算机中去?
使用数据结构:数据的逻辑结构、存储结构、数据的操作(数据的运算)
数据:不再是单一的数值,而是类似集合
结构:数据元素之间的关系
2)采用什么方法解决?
算法
数据结构+算法=程序
1.数据结构
数据结构是数据的逻辑结构、存储结构、数据的操作(数据的运算)
1.1 数据
数据:不再是单一的数值,而是类似集合。(ex:英雄联盟中的英雄)
数据元素:是数据的基本单位,由若干个基本项组成。(ex:英雄联盟里面组成英雄这个整体的每一个英雄)
数据项:数据的最小单位,描述数据元素的信息。(ex:每个英雄的皮肤、技能等等)
节点:就是一个个的数据元素。
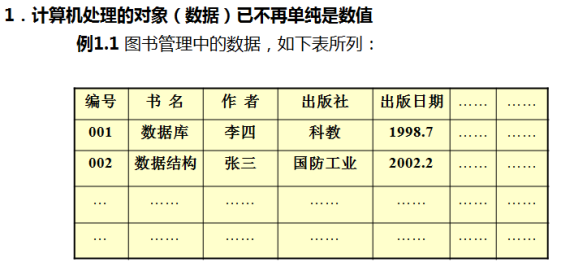
每一行是数据元素,每一列是数据项。
1.2 逻辑结构
逻辑结构:元素和元素之间的关系。
数据的逻辑结构有线性结构、树形结构、图状结构三种。
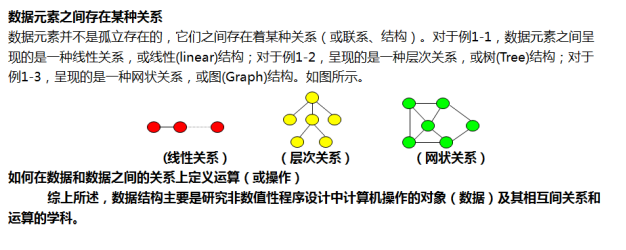
关系 | 结构 | 特点 | 应用 |
线性关系 | 线性结构 | 一对一 | 线性表 |
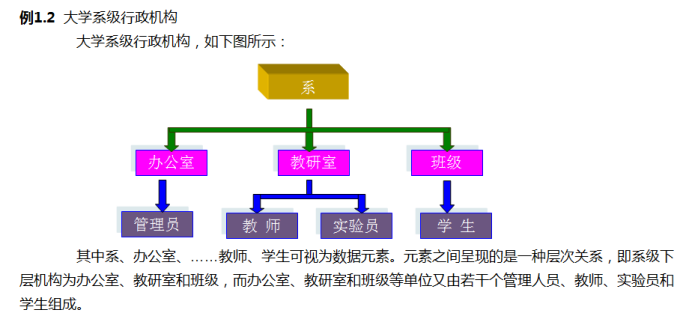
层次关系 | 树形结构 | 一对多 | 树 |
网状关系 | 图状结构 | 多对多 | 图 |
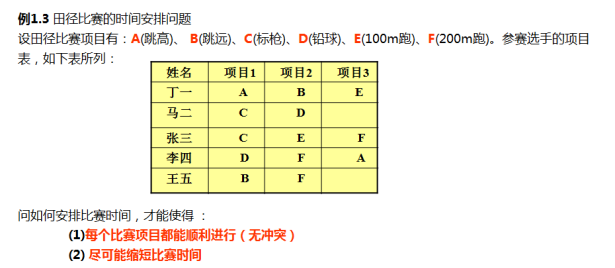
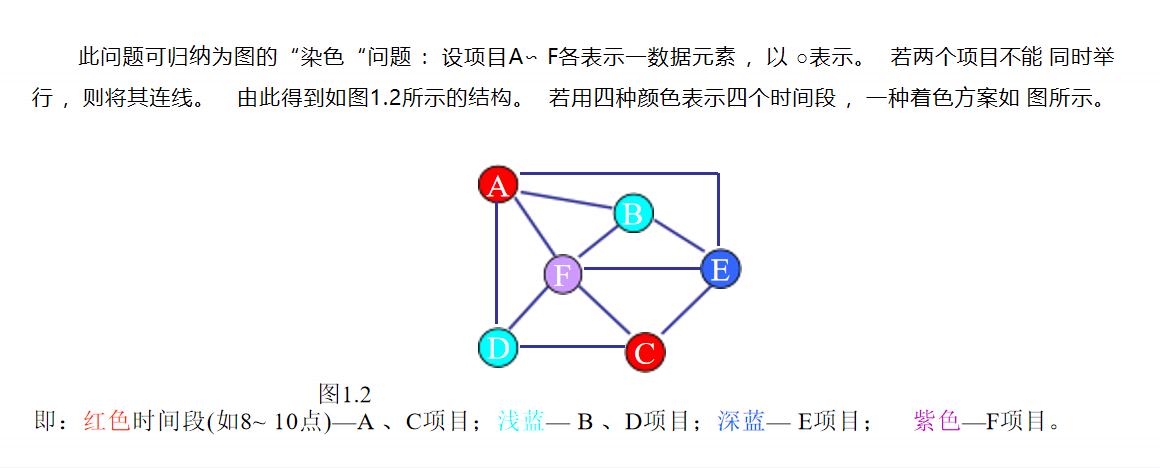
【思路】先看每个项目与其他的哪个项目有冲突:
A与B、D、E、F有冲突,所以A可以与C组合;
B与A、E、F有冲突,所以B可以与C、D组合;
C与D、E、F有冲突,所以C可以与A、B组合;
D与A、C、F有冲突,所以D可以与B、E组合;
E与A、B、C、F有冲突,所以E可以与D组合;
F与A、B、C、D、E都有冲突,所以不能组合。
再对不冲突的项目进行排列组合,则可以有多种安排,例如:
例 | 时间1 | 时间2 | 时间3 | 时间4 |
方案一 | AC | BD | E | F |
方案二 | A | BC | DE | F |
1.3 存储结构
存储结构:数据的逻辑结构在内存中的集体实现。
包括顺序存储结构、链式存储结构、索引存储结构、散列存储结构。
1)顺序存储结构
数组开辟、malloc开辟堆区空间
数组:在内存当中一段连续的内存空间中保存数据(如c语言中的一维数组)
开辟的空间较少;但是固定的开辟一块空间,前后开辟有可能会产生碎片空间,浪费空间。
特点:顺序存储,内存连续。

2)链式存储结构
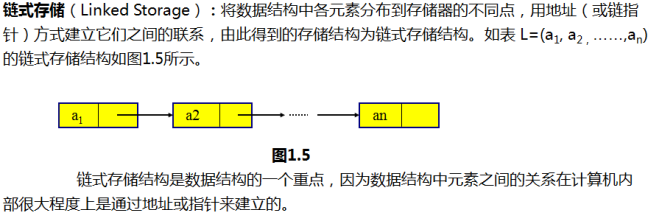
每一个节点(相当于一个结构体变量)都有数据域和指针域(相当于结构体成员),数据域存储数据信息,指针域存储的是下一个节点的地址。
优点是可以利用每一个存储单元,不会产生碎片空间。
特点:内存不连续,通过指针进行连接。
【链表结构体】
struct node_t
{
int date; // 数据域。根据存放数据的类型定义。struct node_t *next; // 指针域。存放下一个节点的地址,是结构体类型指针,指向自身结构体类型。
}
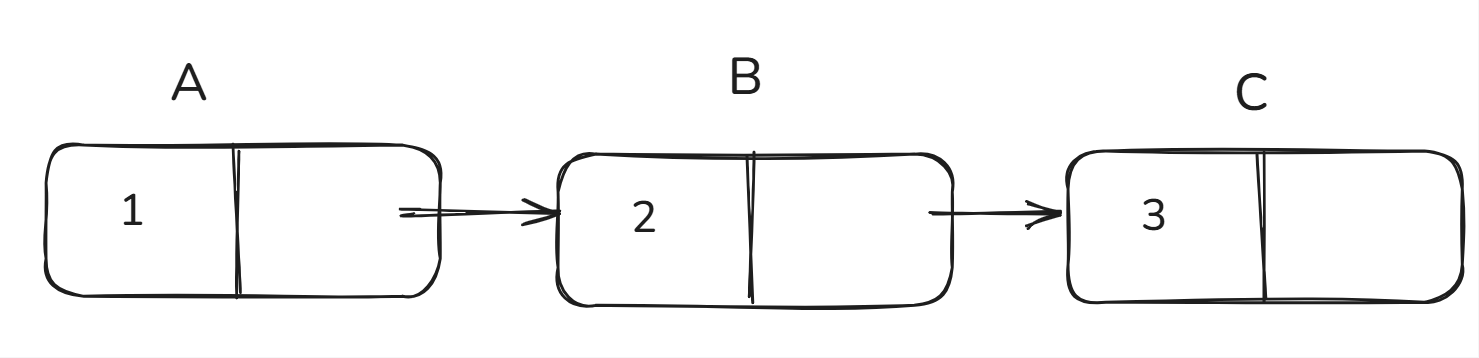
[举例-简单的单向链表]
struct node_t A = {1,NULL};
struct node_t B = {2,NULL};
struct node_t C = {3,NULL};
A.next = &B;
B.next = &C;
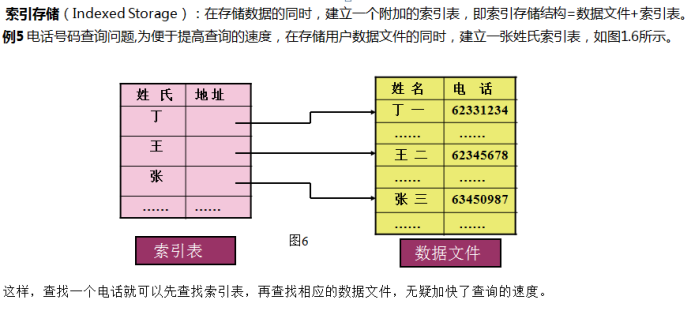
3)索引存储结构
索引表 + 数据文件;
优点:提高了查找速度。
缺点:存储空间占用增多,并且需要增删改时也需要管理索引表增加了部分工作量。
4)散列存储结构
应用:哈希表
数据在存储的时候与关键码之间存在某种对应关系
存的时候按照对应关系存
取的时候按照对应关系取
1.4 操作(数据的运算)
增删改查
2.算法
算法就是解决问题的思想方法。
2.1 算法和程序
程序:用计算机语言对算法的具体实现。
2.2 算法和数据结构
算法 + 数据结构 = 程序
算法的设计:取决于数据的逻辑结构关系。
算法的实现:一定会依赖于所使用的存储结构。
2.3 算法的特性
1)有穷性 // 算法的执行步骤的有限的
2)确定性 // 每一个步骤都是有明确含义的,无二义性
3)可行性 // 算法是能够在有限的时间内去完成的,能获得结果。
4)输入 // 可以有0~n个输入
5)输出 // 可以有0~n个输出
2.4 评判标准
● 如何去评价一个算法的好坏?
1)正确性:保证算法可以正确实现功能,能运行。
2)易读性:容易被自己和他人解读、理解。
3)健壮性:增加容错处理。(增加免疫力)
4)高效性:执行效率。
算法执行快慢容易受到计算机性能的影响,不可以作为评判算法高效性的标准,这通过可执行语句重复执行的次数来衡量算法是否高效 。(时间复杂度:看代码重复执行语句的次数。)
5)低存储性:占用空间少(空间复杂度)。
2.5 时间复杂度
通常时间复杂度用一个问题规模函数来表达:
T(n)=O(f(n))
T(n) // 问题规模的时间函数
n // 问题规模:输入量的大小
O // 时间数量级
f(n) // 算法的可执行语句重复执行的次数,用问题规模n的某个函数f(n)来表达
【例1】求1+2+3+......+n
方法1:
int sum=0;
for(i = 1; i<=n ; i++) //n==1000,1000次
sum += i;
f(n) = n;
T(n) = O(n)方法2:
等差数列{an}的通项公式为:an=a1+(n-1)d。
前n项和公式为:Sn=n*a1+n(n-1)d/2 或 Sn=n(a1+an)/2 。
int sum = n*(1+n) / 2;
f(n)=1;
T(n)=O(1)【例2】
int i,j;
for(i=0;i
时间复杂度:
f(n)=n*n;
T(n)=O(n*n)
【例3】
int i,j;
for(i=0;i
时间复杂度:
i 次数
0 1
1 2
2 3
3 4
n-1 n
f(n)=1+2+3+4+......+n = n*(1+n)/2 = n/2+n*n/2 (重复执行的次数)
保留最高项:n*n/2
除以最高项系数:n*n
T(n)=O(n*n)
【计算O的方法】
(1) 根据问题规模n写出表达式 f(n) // 重复执行的次数
(2) 只保留最高项,其它项舍去
(3) 如果最高项系数不为1,除以最高项系数
(4) 如果只有常数项,直接置1
2.6 空间复杂度
算法占用的空间大小。一般将算法的辅助空间作为衡量空间复杂度的标准。
算法占用的存储空间包括:
1)输入输出数据所占空间
2)算法本身所占空间
3)额外需要的辅助空间





 浙公网安备 33010602011771号
浙公网安备 33010602011771号