地球和太空中无线功率传输的Transmitarrays - 实践
大家读完觉得有帮助记得关注和点赞!!!
摘要:
导言
远距离的无线电力传输 (wpt-ad) 具有实现其中物理连接过于昂贵、机械上不切实际或以其他方式难以实现的应用的巨大潜力。这些包括在两个地球上运行的平台在太空中。空间太阳能发电作为清洁能源的替代来源,允许帮忙应对气候变化带来的日益严峻的挑战。空间太阳能概念,由艾萨克·阿西莫夫在他的短篇小说《理性》中首次提出设想在地球轨道上有一个太阳能发电站,不受昼夜周期或恶劣天气的影响,全年几乎24/7全天候获得阳光。加州理工学院拟议的实施方案包括一个平面的片状电站,该电站涂有柔性光伏器件,该电站启用微波相控阵将收集到的功率发射到地球[22]。因为微波状态受大气的影响很小1,这些位置可以包括使用传统电力基础设施难以到达的区域。就是无论天气状况如何,发电站都可以管用地发射电力,为传统太阳能不切实际的地方提供清洁的太阳能。由电子控制的相控阵列架构提供的另一优点是,功率可以根据需要动态地且同时地分派到不同的位置,具有实时调整功率分配的能力。值得注意的
设计长距离无线电力传输系统时最要紧的挑战是它们的尺寸。衍射极限表明,功率可以聚焦的最小直径与距源的距离成正比,与源的直径成反比。艾里斑半径方程[23]说明了半径均匀照明的透射圆形孔径的这种关系a(此处使用的是半径,而不是典型的直径)。在一个距离右从以波长传输的源λ,主光束的半径 (在第一个零点处测量) 由下式给出 \ begin {方程 *} r_{0} = \ frac{0.61 \ lambda r}{a} \ tag{1}\ end {方程 *}
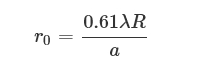
模式中总功率的84%。因此,为了捕获84% 的发射功率,发射机或接收机必须至少与距离成线性比例。例如,在地球静止轨道 (GEO) 中以10 GHz运行的发射机 (∼高于地球表面36,000公里) 需要1.6公里的直径才能将其主光束聚焦到地球上1公里直径的接收站。就是径向积分功率从0到右0大约
这种尺寸的相控阵列中的阵列元件的数量进一步加剧了这种缩放挑战。相位阵列的高效空间功率组合和使用电子转向创建动态焦点的能力使其成为无线功率发射器的理想选择。但是,它们必须密集的元素间距 (∼ λ/2),以避免栅瓣 (所谓的 “稀疏阵列诅咒”),从而导致非常大的元素数量。避免栅瓣对于无线功率传输尤其重要,因为它们导致主要的效率降低。
数十亿个元素,令人生畏。就是此外,元件必须与相同的频率源同步,并且它们的相对相位必须在所有操作条件下保持。需要复杂的分配网络来为这种阵列中的元件提供相位稳定的低相位噪声频率参考。对于其中假定 (有时隐含地) 绝对相位参考以便执行必要的相位共轭的回射阵列也存在该挑战。已经进行了工作以处理与超出典型RF分配网络的相控阵列的大规模同步相关联的挑战。其中包括长距离低损耗分布的光分布手艺和用于分布式阵列同步和定时对准的无线技术。尽管如此,同步大量元素的前景,在空间太阳能发电的情况下可能
应对这一挑战的一种方法是应用作为无源中继器工作的transmitarray重新聚焦从发射器 (以下称为有源阵列) 到接收器的功率,如图所示。1电子可调谐移相器和基本数字控制。就是。有源阵列聚焦到作为微波透镜的透射阵列,重塑波前并将光束重新聚焦到接收器 (或再聚焦到另一个transmitarray以形成多级中继链)。由于透射阵列重新聚焦有源阵列的波束,因此可能在不增加整流天线阵列的尺寸的情况下使有源阵列明显更小。出于两个原因,这是期望的。开始,与有源阵列不同,transmitarray不需要同步,因为入射波前是transmitarray的参考。其次,透射阵列比有源阵列便宜得多,缺少后者的许多有源组件和复杂性。请注意,transmitarray是无源中继器; 它不会向波束引入新的能量,也不会修改波束的频率。透射阵列所需的唯一电子组件
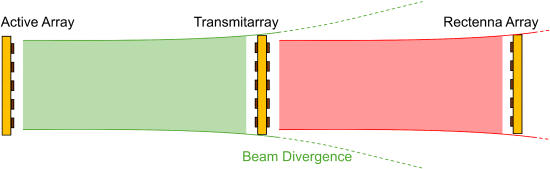
Transmitarray无线电力传输体系。transmitarray重新聚焦来自发射器的发散光束,扩展其范围。
在这项工作中,我们提出了一种10 GHz的空间太阳能概念,该概念由对地静止轨道 (GEO) 中的相控阵的多轨道星座和中地球轨道 (MEO) 中的透射阵列组成。根据最近在X波段进行的无线功率传输研究的趋势,选择了10 GHz。使用物理光学和技术经济分析,建立了系统的成本模型。表明,对于某些有源阵列直径,将透射阵列用于空间太阳能可以大大降低体系的LCOE。
硬件解决方案
对于天基太阳能发电系统,环境效率和成本以及空间太阳能电站的物理灵活性和面积质量是决定系统实用性的驱动因素。许多解决方案,最大限度地减少面积质量和成本,同时最大限度地提高不同系统组件的效率和灵活性。虽然这项研究的大部分涉及有源相控阵,但由于它们之间的相似性,许多技巧都延续到透射阵列。
中探索的相控阵分层方式是满足对灵活性和面积质量的严格要求的一种方法。然而,为了增加灵活性和机械鲁棒性,我们将我们的设计空间限制为没有层间电连接的分层设计,而是依赖于层之间的电磁耦合。我们考虑了两种符合我们目标的可能的设计方法: 频率选择表面方法和接收器-发射器方法。我们证明后者对于我们的独特应用是可取的。
A.多层频率选择表面法
Ml-fss由N,任意图案化,导电层由基板隔开。气隙基板非常适合我们感兴趣的大型,灵活,可折叠的结构。3不幸的是,正如所讨论的[34],ml-fss涉及层数,传输损耗和传输相移范围之间的固有权衡。这种权衡在传输线模型中最为明显,其中ml-fss中的每一层都由具有ABCD参数矩阵的单个无功分流不连续性表示
在哪里B是并联阻抗的电纳。通过就是计算S参数的幅度和相位,我们发现这两个分量不是独立的,而
改变传输相位必然导致传输幅度的改变。这意味着对于给定的损耗量,在可实现的相位范围上存在上限。例如,如果我们需要|S21|2>0.9(<1dB损耗),只能实现52度的相位范围,与期望的360度相差甚远。
参考经验上将此结果扩展为2层、3层和4层ml-fss设计相同,如果允许不相同的层,则可以用3层获得360度相位范围。然而,这种设计需要对所有三层进行单独的、独立的控制,从而大大增加了数字布线要求。就是图层。特别地,它们证明需要4层ml-fss来实现具有小于1dB的损耗的360度传输相位范围。重点的
B.接收机-发射机方法
接收器-发射器方式借助打破支撑传输线模型的假设,即,克服了ml-fss方法的局限性。当入射波通过透射阵列传播时,入射波保持在TEM模式。这种方法应用由传输线耦合的两个背对背天线,如。对于跨阵列的相移梯度固定的静态透射阵列,改变跨阵列的传输线长度会引入相位梯度; 对于可重构透射阵列,沿着传输线添加可编程移相器。而在ml-fss中,每一层都对传递函数贡献一个极点,可以使用集总元件和/或传输线段沿着传输线将任何数量的极点引入接收器-发射器透射阵列。利用三个机械层 (两个天线层和一个传输线层),可以实现任意相移范围,仅受传输线和移相器中的损耗的影响。这些损失并非微不足道,但并不像ml-fss那样从根本上受到限制,如(3)。
为了验证我们的结论,我们设计并仿真了静态接收器-发射器3层传输阵列4晶胞,工作在10 ghz。由于这种设计满足了我们独特的一组要求,因为它是灵活的,在层之间没有电互连,并且可以实现低于1dB的损耗,它可以作为未来设计无线功率传输透射阵列的起点。
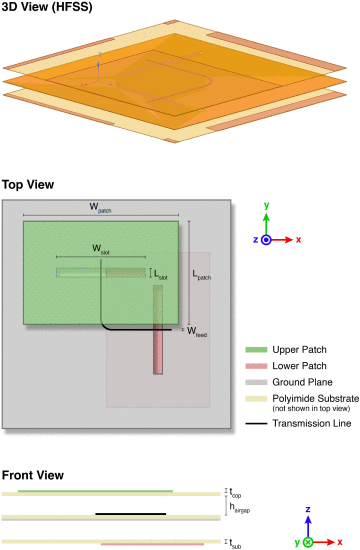
各层如下 (见图。2):
接收贴片天线
由聚酰亚胺基板分隔的传输线和接地平面
发射贴片天线
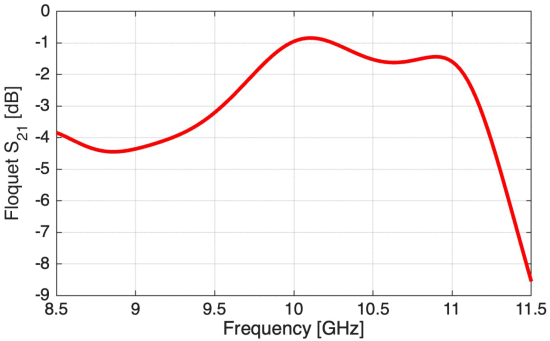
法向入射下透射阵列晶胞的模拟S21。
成本分析
A.物理光学模型
虽然基于晶胞的无限阵列模拟对于设计晶胞本身很有效,我们寻求另一种工具来对具有大量元素的数组的效果进行建模,这些元素的范围仍然有限。由于空间太阳能系统中阵列的尺寸远大于波长,因此物理光学是分析它们的合适工具。特定是,由于透射阵列,有源阵列和整流天线阵列位于彼此的辐射近场区域中,因此我们使用菲涅耳衍射模型。
如图所示。4,我们与预计彼此平行且与传播方向正交的源平面和图像平面。这使我们能够在大转向角下计算近似衍射图案。重点的是要注意,对于一个任意的光圈来引导专注波束到空间中的特定点,它必须引入两个相位梯度: 线性梯度在特定方向上引导波束,并且二次梯度将波束聚焦在距孔径给定距离处。
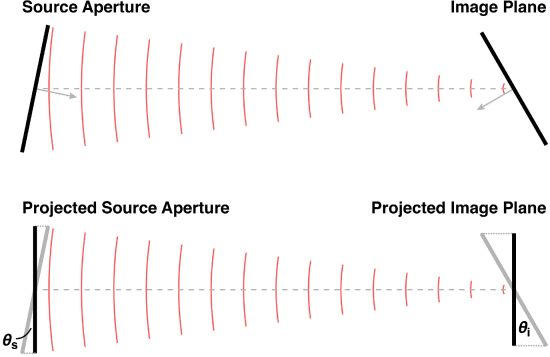
我们近似的几何形状允许将菲涅耳衍射公式应用于大衍射角。
显示全部
为了计算模式,我们遵循该简单的过程:
将源孔径替换为其在投影孔径平面上的投影,即通过cosθs。因为投射的源垂直于传播方向,所以线性相位梯度被从相位分布中去除。
计算投影孔径的菲涅耳衍射图样
“取消投影” 源平面,即拉伸图案1/cosθ我
为了验证其有效性,我们对该手段进行了测试,并将其与惠更斯-菲涅耳原理进行了比较。独特是,我们将圆形区域中的积分功率作为圆半径的函数进行了比较。我们发现即使在大衍射角下,偏差也小于1% (∼ 50∘)。径向积分功率度量对于无线功率传输是重要的,因为我们最终关心给定半径的接收器捕获多少功率。
B.单位面积成本模型
一旦计算出衍射图案,我们就可以确定接收孔径 (无论是透射阵列还是整流天线阵列) 捕获的功率量,作为该孔径面积的函数。因为我们最终想要最小化一些成本函数,故而我们运用每单位面积成本将每个阵列的面积与其总成本相关联。对于有源阵列和整流天线阵列,我们依赖于[22](参见表2,“中间” 列) 来计算有源阵列和整流天线阵列 (地面站) 的单位面积成本。单位面积成本的计算方法是将每个阵列的总成本除以 (COSTtotal=COST我n我t我al+15⋅COSTannual) 按每个数组的面积计算。对于有源阵列,我们获得ctx=354$/m2,对于整流天线阵列,crx=121$/m2。这些值自然假设所有成本与面积线性缩放,只要阵列都不会变得太大或太小,这近似为真。
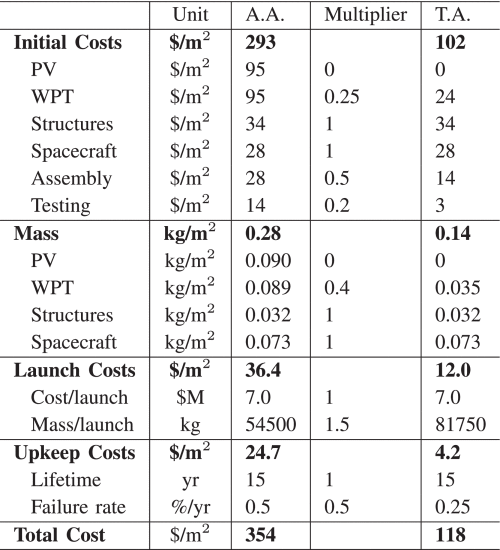
因为transmitarrays不是的一部分[22],由于transmitarray和有源阵列硬件之间的许多相似之处,我们使用有源阵列成本细分作为我们的transmitarray成本模型的基础。在表中2GEO中。就是我们将transmitarray成本分解为初始,启动和年度维护成本 (transmitarray模块更换),并说明如何从有源阵列成本模型中得出这些成本。WPT成本和质量的降低是由于缺少RF集成电路、弹出式天线和重型DC传输线。由于透射阵列比有源阵列复杂得多,因此还降低了组装、测试成本和故障率。最后,每次发射的质量增加,因为传输阵列位于MEO而不
由于与GEO相比,MEO中的辐射效应更高,因此比有源阵列更昂贵的透射阵列的一部分将是辐射屏蔽。然而,基于绝大多数的透射阵列是无源的,所以电子器件所需的附加屏蔽是小的。
C.Transmitarray星座
通过在由一个有源阵列、一个发射阵列和一个整流天线阵列组成的系统中,该环境将仅能够按照预期针对发射阵列的轨道的一小部分进行操作。当transmitarray绕地球运行时,它将周期性地接近活动和整流天线阵列之间的视线路径,穿过该路径,然后移开,最终被地球黯然失色。对于其中透射阵列与其他两个阵列或多或少对齐的小轨道段,能够按预期发生通过透射阵列的透射 (参见图5(a))。否则,transmitarray处的到达/离开角以及阵列之间行进的额外距离都将导致能量损失,从而使transmitarray几乎无用 (参见图5(b))。
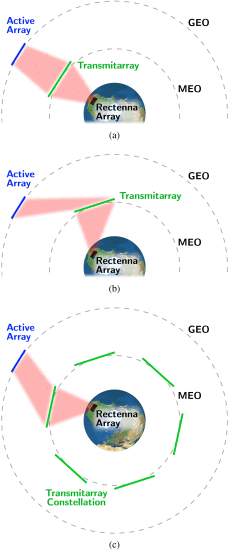
显示 (a) transmitarray与功率传输方向对齐时的功率传输,(b) transmitarray与功率传输方向不对齐时的功率传输,以及 (c)应用transmitarray星座进行功率传输-有源阵列现在可以通过与功率传输方向更紧密且更好地对齐的transmitarray进行波束传输。
显示全部
为了避免此种能量损失,我们提出了一个星座N助教等间距的透射阵列占据相同的轨道。当一个transmitarray从有源阵列移开时,另一个transmitarray将接近,以便当第一个移出范围时,有源阵列将迅速将其波束重新聚焦到下一个transmitarray (见图。5(c))。虽然这会增加系统的总成本,但会降低其LCOE。例如,如果单个transmitarray只能用于其轨道的1/5,则使用5的transmitarray星座将使发射到地球的能量增加5倍。同时,该架构的总成本增加了远小于5倍。
我们还建议增加活动阵列和整流天线阵列的数量,以匹配透射阵列的数量 (见图。6)。如果仅使用一个有源阵列和整流天线阵列,则在给定时间将仅使用一个透射阵列,从而导致显著的开销。可以借助将每个未使用的transmitarray与其自己的有源阵列和整流天线阵列相匹配来消除这种开销 (当然,给定有源阵列使用的特定transmitarray将随着transmitarray的轨道而改变)。这个三重星座将进一步降低LCOE: 相对于具有10个透射阵列但只有一个有源阵列和整流天线阵列的系统,与10个透射阵列一起使用的10个有源阵列和整流天线阵列的星座将框架的总能量输出增加10。但是,系统的总成本明显增加了不到10倍,这意味着LCOE必须降低。
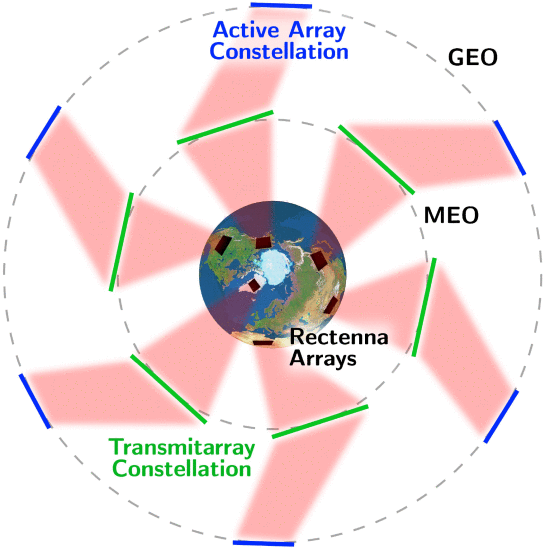
卡通表现了一个完整的星座,包括有源阵列,transmitarray和整流天线阵列。当透射阵列移动利用它们的轨道时,有源阵列连续地调整它们的波束以聚焦在最近的透射阵列上。
显示全部
完整的星座图如图所示。6其中每个数组有6个。每个活动阵列将始终引导到最接近的transmitarray。当transmitarray绕地球运行时,有源阵列将周期性地将其波束重新聚焦到下一个transmitarray。
D.结果
较大,源于得如前面部分所讨论的星座。另一方面,增加一个transmitarray星座就是如开发于[22],系统的LCOE和框架的总成本是两个可能的成本函数。当应用transmitarray时,系统的总成本老can否有利。就是降低LCOE。当然,如果仅考虑LCOE,则应使用最大可能的有源阵列。显然,这是不切实际的,因为可能由于同步挑战,将存在一些实际的最大活动阵列大小。由于正在进行大规模阵列同步方案的研究,因此我们将活动阵列大小作为分析中的自变量。对于每个有源阵列大小,我们计算有和没有透射阵列的系统成本,以确定对于该特定有源阵列,透射阵列
用于计算LCOE的代码采用以下参数:
活动数组的大小: 自变量
所需的transmitarray捕获效率:ηTA,cap=0.7(捕获效率指定入射在透射阵列上并由透射阵列捕获的有源阵列的辐射功率的百分比。)
发射器阵列的内部效率 (包括移相器和天线的损耗):ηTA=0.9
星座中有源阵列/透射阵列/整流天线阵列的数量:
N=10
工作频率: 10 ghz
阵列轨道/位置: 活动阵列位于GEO中,整流天线阵列位于活动阵列的正下方,透射阵列位于MEO中,高度为GEO的一半
阵列方向: 活动阵列和transmitarrays指向最低点
transmitarray离散轨道上的点数
由于非统一捕获效率以外的因素而导致的体系效率。这包括光伏损耗、直流到射频转换损耗、整流损耗等: 6% (见[22])
通过通过启用更大的星座来建立的。就是我们忽略了大转向角下的偏振失配和附加损耗的影响。后者可能是由于天线元件图案和由互耦变化导致的阻抗失配。这些因素有可能增加损失,超出此处考虑的范围,但可以减轻。通常依据使用圆偏振来减轻偏振失配。能够借助限制最大扫描角来减少大扫描角处的挑战; 在该系统中,这
给定上述参数,程序计算可实现的最小LCOE。程序选择最小LCOE,基于整流天线阵列大小不固定; 对于每个整流天线大小,都有不同的LCOE。然而,transmitarray的大小是通过指定间接固定的ηTA。该算法的摘要如下。
管用发射阵列轨道跨度计算为360∘/N。由于衍射图案是周期性的,因此轨道跨度是实际用于计算的transmitarray轨道的一部分。
有源阵列的聚焦和转向衍射图案是在transmitarray的位置处针对transmitarray的轨道跨度中的每个点计算的 (参见图7中排)。
根据衍射图案计算出透射阵列的捕获功率随其直径的变化。
确定transmitarray的大小以满足指定的捕获效率参数。
对于透射阵列轨道跨度中的每个点,在整流天线阵列的位置处计算透射阵列的聚焦和转向衍射图案 (参见图7底行)。
整流天线阵列的捕获功率作为其直径的函数是根据衍射图案计算的,并且根据衍射图案计算的LCOE是直径的函数。
最后,选择整流天线阵列大小以最小化LCOE。
此过程的关键部分是计算透射阵列上的有源阵列和整流天线阵列上的透射阵列的衍射图案。示例性图案在图i中示出。7周期性的,因此做出此假设会大大减少计算时间。仅必须为一个活动阵列/transmitarray/rectenna阵列集计算模式,并且仅需要为transmitarray轨道中最接近活动阵列的部分计算模式,即,有效轨道跨度360∘/N。就是。大家假设有源阵列,透射阵列和整流天线阵列在地球周围周期性地间隔开。即使整流天线不一定是周期性的,但由于每种阵列类型的周期性意味着模式本身在transmitarray移动通过其轨道时
在无花果中。8(a),大家表明了最小LCOE,LCOE最小,这可以依据3层星座来实现。我们还绘制了在只有一个有源阵列和整流天线阵列但没有透射阵列的系统中可以实现的最小LCOE (黑色虚线)。与没有透射阵列的平台相比,LCOE的百分比增加/减少在图i中示出。8(b))。这是一个关键的比较,因为它告诉我们哪些平台 (就有源阵列直径而言) 受益于使用transmitarray。我们得出的结论是,将透射阵列引入系统可将有源阵列直径的LCOE降低到大约以下∼此特定参数组为1000 m。
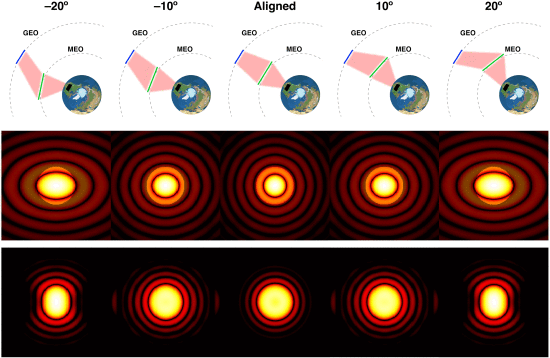
当透射阵列移动通过其轨道 (顶部) 时,有源阵列在透射阵列平面 (中间) 和透射阵列在整流天线平面 (底部) 的五个点的衍射图案。有源阵列图案中落在transmitarray之外的部分变灰; transmitarray将圆圈中的功率重新辐射到整流天线阵列。在这种情况下,N=9因此,每个transmitarray的有效轨道跨度为40∘。
显示全部
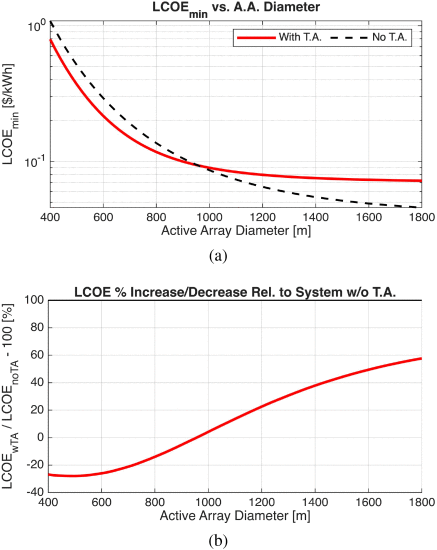
成本分析结果。A.A. = 活动阵列。T.A. = transmitarray。对于每个有源阵列直径,我们绘制 (a) 具有和不具有透射阵列的最小可实现的LCOE,以及 (b) 相对于不具有透射阵列的LCOE增加/减少百分比。
显示全部
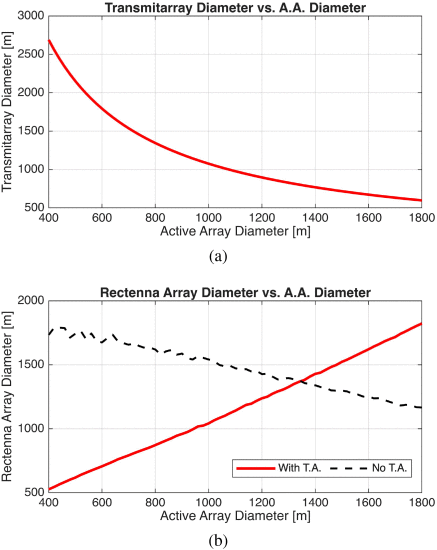
直观地说,这是由于衍射图案相对于其源尺寸的逆缩放引起的。由于有源阵列照亮了transmitarray,因此transmitarray直径与有源阵列直径成反比。9(a))。同样,整流天线阵列与transmitarray成反比,因此它必须直接与有源阵列成比例 (见图。9(b))。如果有源阵列做得极其大,则传送阵列将变得非常小,得采用非常大的整流天线阵列。在某些时候,transmitarray将足够小,以至于最好直接向地球发射光束。
该分析的一个重要的副作用是,在透射阵列有利的情况下,架构在地面上将具有非常小的光斑尺寸,如图i所示。9(b)相当有价值的。小型整流天线阵列也可用于军事应用和自然灾害救济。小型临时整流天线阵列可以非常快速地构建,并且在不再需要时同样高效地拆除。就是。对于土地溢价可用的位置,这可能
使用transmitarray系统的缺点是双重的。最初,transmitarray的大小有效地替代了活动数组的大小。因此,透射阵列的尺寸非常大,如图3所示,直径在1-3km的数量级。9(a)。只是,我们注意到,构造这种大小的transmitarray比构造类似大小的有源阵列要可行得多,因为不需要同步方案。其次,要实现图1所示的LCOE。8(a),架构需要在每个级别上有10个阵列的星座。随着星座大小超过10,图中的两条曲线之间的间隙。8(a)增长,但只到一个点。倘若星座大小被充分地减小,则间隙将闭合,并且将不存在其中透射阵列是有益的任何点。这表示总系统成本和复杂性与系统的LCOE之间的权衡。
发射阵列原型
上述成本分析的一个重要假设是,可以廉价地制造透射阵列,并且面积质量非常低。为了证明重量轻且价格合理的透射阵列的可行性,我们使用低成本,标准,商业柔性PCB工艺和低成本现成材料制造了静态透射阵列。该原型的设计依赖于用于transmitarray设计的更常见的ml-fss手段,因为该原型的目的是说明该PCB工艺的可行性,而不是创建一个非常低损耗的transmitarray。
每一层都由一个柔性单层PCB组成,每个PCB都构建在一个25μm厚的聚酰亚胺基板与1/2盎司铜。采用具有1.12的测量介电常数和可忽略的损耗的低成本EVA泡沫在各层之间保持2 mm的间隙。电磁,传输阵列是一个16 × 16λ/2单位单元网格,其中每个单元由经过缝隙耦合的两个相同的贴片天线 (外部两层) 组成 (图10)[40],[41]。通过跨透射阵列在4 mm和9 mm之间改变缝隙长度来引入相位梯度。制造的原型的照片如图所示。11。
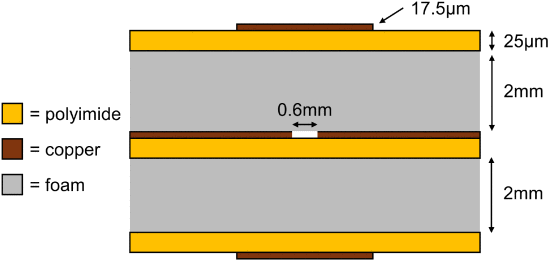
Transmitarray原型堆叠。外层是在中间具有用于耦合的槽的贴片天线。
显示全部

制造的透射阵列原型: 单个层 (左) 和组装阵列 (右)。
显示全部
为了测量透射阵列的聚焦能力,大家使用位于透射阵列正后方2.5 m处的256元素相控阵对其进行了照明。在transmitarray另一侧1.3m的距离处,应用近场扫描仪测量在大约1 m × 1 m的正方形上的功率分布,无论是否放置了transmitarray (图13)。测量设置如图所示。12。与相控阵本身相比,发射器阵列将峰值功率密度提高了3.5db,并将-3dB波束面积降低了约75%。

原型透射阵列测量设置。
显示全部
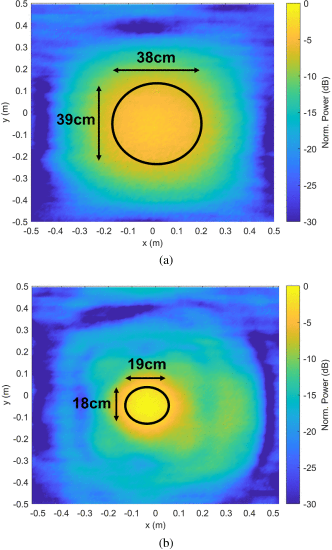
(a) 没有透射阵列的归一化功率密度和 (b) 具有透射阵列的归一化功率密度。将强度值归一化为测得的最大强度与transmitarray。黑色椭圆对应于每个图各自峰的-3db等高线。
显示全部
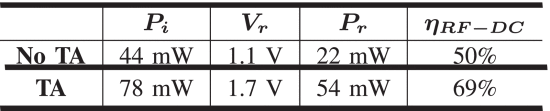
为了演示transmitarray提高传输到整流天线阵列接收器的功率的能力,0.5λ间距 (7.5cm × 7.5 cm) 整流天线阵列[7]使用探头扫描仪将其放置在主光束的中心。使用闭环反馈算法将相控阵聚焦到整流天线,以最大化功率传输[30]聚焦时整流带处的电压图如图所示。14。峰值整流电压,V右,它馈送到一个54Ω负载增加1.54倍,对应于整流功率增加2.37倍,P右。
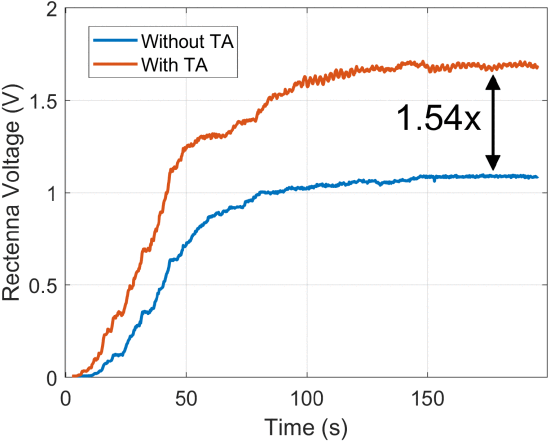
聚焦时整流天线输出电压。Retenna DC输出由54终止Ω负载在这两种情况下。
显示全部
表提供了整流器测量的摘要3。源于整流条的效率,η右F−DC,作为入射功率的函数而变化,P我,需更多的信息才能说明P右意味着增加P我。通过对图中的功率测量进行积分。13在整流带区域,我们发现P我当添加整流天线时,增加了1.77倍,确认了transmitarray是否增加整流带的功率密度。因此,2.37倍的增长P右部分原因是效率从50% 提高到69%[7]部分原因是由于transmitarray的聚焦。
结论和今后的工作
任何无线功率传输架构中的首要问题。在平台级别,成本分析表明,transmitarray可以通过降低平台的LCOE来提高空间太阳能发电的可行性,从而降低向消费者给予的电力成本。在灵活性方面,transmitarrays还减小了地面整流天线阵列的尺寸,增加了系统在紧急和军事应用中的潜力,在这些应用中,敏捷获得电力至关重要。最后,我们以实际演示作为结论,该演示表明低成本,低质量的透射阵列可以显着增加无线功率传输系统中传输的功率量。就是上面我们供应了在无线功率传输,特别是空间太阳能的背景下对透射阵列的理论讨论。我们提供了transmitarray晶胞设计的初步工作,该设计可实现大范围的传输相位设置,同时保持低损耗,这
在无线功率传输的背景下,对透射阵列的未来工作可能包括第节中讨论的设计的制造二以及替代设计。关于成本分析,本文忽略的一个重要变量是工作频率。如中的频率分析所示[22],最佳频率的演算可以根据成本函数而显着变化。我们预计,做一个包括频率的成本研究将表明,在给定衍射的其他频率下,进一步的LCOE降低是可能的 lambda-依赖。
但是,即使仅考虑单个频率,大家也认为我们的结果表明,透射阵列可以在经济上可行的空间太阳能系统的实施中发挥重要作用。更重要的是,它们可能被证明是从技术角度依据降低同步要求来实现空间太阳能发电的关键,这是当今空间太阳能发电面临的最重大挑战之一。本文介绍的工作可以作为富有成效的讨论,研究和开发的起点,使我们更接近从太空提供清洁太阳能的愿景。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号