实用指南：2025牛客多校第六场D题解

题目大意：

给出大小为 $n\ast n$ 的矩阵 $A$，需满足以下要求。
1.元素均小于等于$m$ ；
2.第一行元素全为0，每行元素单调不减
3.对于任意的$1\le i<k\le n$ 和 $1\le j<l\le n$，均有 $A_{i,j}+A_{k,l}\le A_{i,l}+A_{k,j}$
4.$1\le n,m\le 5\times 10^5$
将符合的方案数对 998244353 取模。

首先，大家观察$A_{i,j}+A_{k,l}\le A_{i,l}+A_{k,j}$这个式子，可以对其进行公式的转换，令$k=i+1$，$l=j+1$，及 $A_{i,j}+A_{i+1,j+1}\le A_{i,j+1}+A_{i+1,j}$，进一步转换为$A_{i+1,j+1}-A_{i+1,j}\le A_{i,j+1}+A_{i,j}$通过，之后我们能够用差分数组$b_{i,j}$ 来表示 $A_{i,j+1}-A_{i,j}$，则有 $b_{i+1,j}\le b_{i,j}$，及位于同一列的差分元素单调不增，又基于题目所说的每行元素单调不减，也就相当于每行的差分元素均大于0，而给个元素小于$m$的条件也就相当于第一行的差分数组相加之和不大于$m$，至此，题目所求转换为以下内容：

求满足一下条件的大小为$n\ast (n-1)$的矩阵 $b$ 的个数。
1.第一行的所有元素相加不大于$m$.
2.满足$b_{i+1,j}\le b_{i,j}$，及同一列的数组单调不增。

形象化的
我们不妨以第一列为例子，设第一列第一行的元素为$x$，及 $b_{1,1}=x$通过，第一列大家能够在用一个差分数组$c$ 来表示，及 $c_{i,j}=b_{i,j}-b_{i+1,j}$，那么同一列中所有的$c$数组元素相加总和为$x$，那么对于差分数组$c$，其构成相当于将元素$x$分为行为空的$n$份，并使得每份的相加之和为$x$，用隔板法的思想进行求解，那么方案数为$\left(\genfrac{}{}{0ex}{}{x+n-1}{n-1}\right)$。

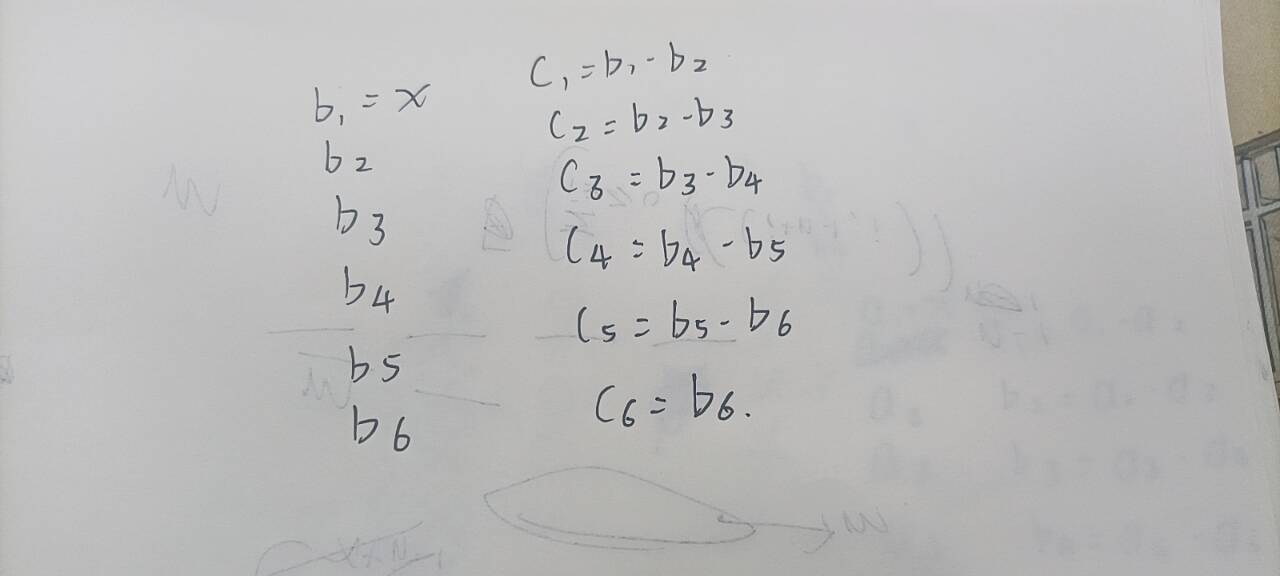
大家现在已经知道了第一列的求法了，那么我们如何推广到每一列呢？考虑到对于第一列的求法，其形式相当于将$b_{1,1}$个相同的小球放入$n$个盒子中，那么对于第$j$ 列，也是将 $b_{1,j}$个相同小球放入$n$个盒子中，且满足${\sum }_{i=1}^{n-1}{b}_{1,i}\le m$，因为每一列的求解是相互不会影响的，那么我们就可以想到将 0 到$m$个相同小球放入$n\ast (n-1)$个盒子的方案数，缘于转换为差分数组$c$后，矩阵中所有的差分数组$c$的总和即为第一行的差分数组$b$的和，换句话说，设第一行的数组$b$的总元素和为$ans$，再将 $ans$用隔板法分成可以为空的$n-1$份，然后对于每个分配的值再进行上述的分别隔板，其方案等价于将$ans$个相同的小球分成允许为空的$n\ast (n-1)$份，方案数为${\sum }_{i=0}^m\left(\genfrac{}{}{0ex}{}{i+n\ast (n-1)-1}{i}\right)$

对于上述式子借助递推的方式已经可以过了，当然也可以对其进行进一步的更改，相当于将$m$ 个小球放入 $n\ast (n-1)+1$个盒子的方案数，多出来的一个盒子是用来存放不需要的小球的，也就相当于前面的放入方式，那么总的方案数为$\left(\genfrac{}{}{0ex}{}{m+n\ast (n-1)}{m}\right)$。