树状数组学习笔记。在前面的文章我们学习了数组数组，也写了一篇学习笔记，树状数组一般就是用于范围增加单点查询，虽然范围增加范围查询也可能做，但是不如线段树方便。而线段树除了能支持范围增加、范围查询，可以帮助在 O(logn) 时间内完成多种在线区间操作，例如区间求和、区间最大值、区间最小值、区间重置左程云算法讲解110【扩展】线段树专题1-线段树原理和代码详解。

文章目录

1. 什么是线段树
2. 线段树结构和代码（区间和为例）
- 2.1 线段树查询
- 2.2 线段树更新
3. 题目

1. 什么是线段树

前置文章：树状数组学习笔记。在前面的文章我们学习了数组数组，也写了一篇学习笔记，树状数组一般就是用于范围增加单点查询，虽然范围增加范围查询也可以做，但是不如线段树方便。而线段树除了能支持范围增加、范围查询，可以支持在 O(logn) 时间内完成多种在线区间操作，例如区间求和、区间最大值、区间最小值、区间重置等操作，总之就是树状数组能做的线段树都能做，学习视频地址：左程云算法讲解110【扩展】线段树专题1-线段树原理和代码详解。

2. 线段树结构和代码（区间和为例）

首先来看下线段树的结构，假设现在有一个数组 [1，2，3，4，5，6，7，8]，我们要维护区间查询信息，就可以构建出线段树，如下图所示：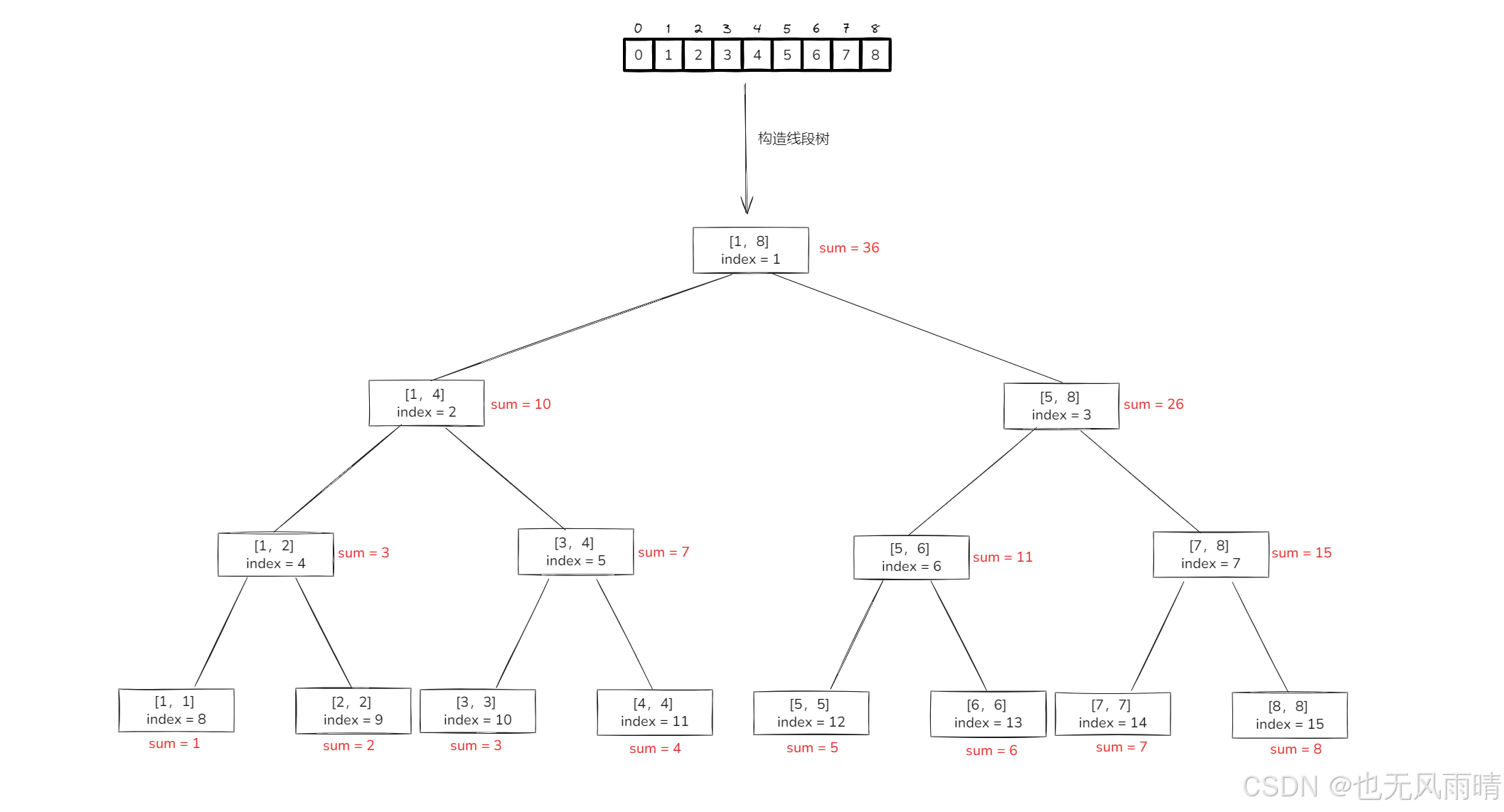

可以看到，上面构建出来的就是 维护区间求和 的线段树的结构，线段树也是用数组来存储，index 就是数组下标，上面的区间表示这个下标维护的是哪个区间的总和，比如根节点 index = 1 维护的就是范围 [1，8] 的总和。

每一个节点的孩子节点分别维护了一半区间的求和，假设当前节点是 i，那么左右子节点就是：i * 2 和 i * 2 + 1，需要注意的是这个规则要求下标从 1 开始，因此后面出现线段树的题目都是从下标 1 开始计算的。

那么对于线段树，维护长度为 n 的数组需要多少空间呢？可以看这篇文章，说的比较详细：线段树基础 OI。总之就是如果输入 n 个数字，要维护这 n 个数字直接开 4n 的空间就行。

对于线段树，由于 n 个节点，加上补齐的没用节点之后可以构造出一棵完全二叉树，而我们知道完全二叉树的节点个数为： $2^h - 1$ ，其实 h 就是高度，对于完全二叉树节点是 k 的情况下，最终可以得到 $k = 2^h - 1 => h = log_2{(k+1)}$ 的时间复杂度来算出，当然了由于 k 肯定是最大值的情况，所以最终不管是查询还是范围修改，都可以在 $log_2n$ 的时间复杂度内完成。下面来看下树的构造方法以及参数。

// 数组最大值
public static int MAXN = 100001;
// 原数组
public static long[] arr = new long[MAXN];
// 线段树，维护区间和
public static long[] sum = new long[MAXN <<
2];
// 线段树区间增加的维护数组
public static long[] add = new long[MAXN <<
2];

sum 就是线段树数组，用于维护区间总和信息，arr 就是数组信息，我们上面说过 n 个数字对应的线段树大小直接开 4n，所以 sum 的长度就是 MAXN << 2，这个 MAXN 是根据题目的最大值设置的，不同题目有不同的值。add 数组是添加数组，用于线段树范围增加的，后面 2.2 小节会说，这篇文章就是以线段树区间增加，区间查询为模板。然后下面就是 build 方法，build 方法用于构建线段树。

// 递归建树
public static void build(int l, int r, int i) {
if (l == r) {
sum[i] = arr[l];
} else {
int mid = (l + r) >>
1;
// 递归左边建树
build(l, mid, i <<
1);
// 递归右边建树
build(mid + 1, r, i <<
1 | 1);
// 求出当前 i 节点的 sum 累加和信息
up(i);
}
// 初始化 add 数组
add[i] = 0;
}
// 维护当前节点的累加和
public static void up(int i) {
// 父节点的累加和 = 左子节点的累加和 + 右子节点的累加和
sum[i] = sum[i <<
1] + sum[i <<
1 | 1];
}

2.1 线段树查询

上面就是线段树的结构了，下面来看下线段树查询，假设现在我们要查询区间 [2，7] 的总和，那首先就是从根节点出发了。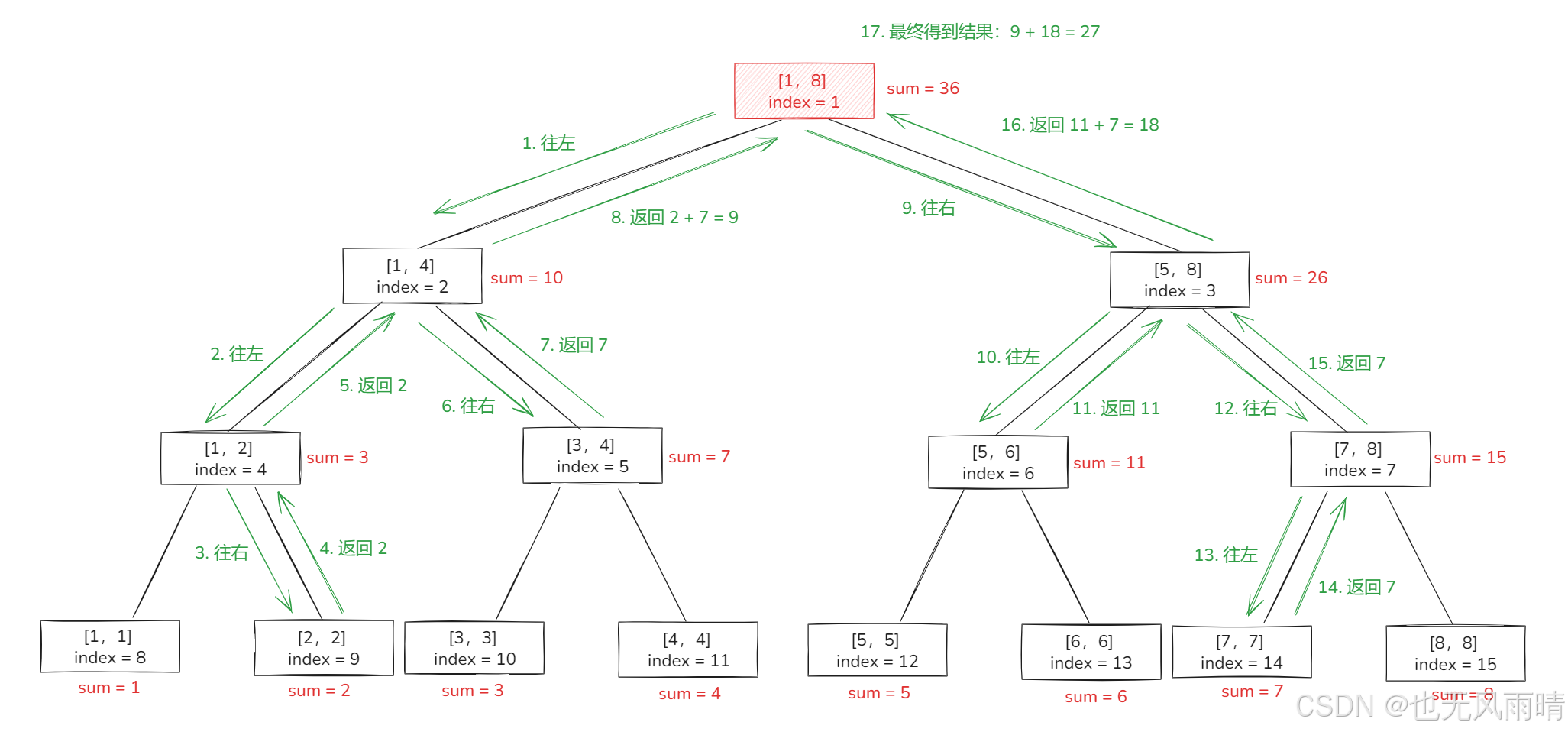

查询的流程如下：

从根节点出发往左遍历，来到 [1，4] 这个范围，发现 [2，4] 在这个范围内，且需要继续往左遍历。
往左遍历来到 [1，2] 这个节点，发现 [2] 在这个范围内，需要向右遍历。
向右遍历到 [2，2] 这个节点，发现 [2，2] 在 [2，7] 范围内，返回 sum[9] = 2。
继续返回结果到 [1，4]，向右遍历来到 [3，4]，发现 [3，4] 在 [2，7] 范围内，不再继续往下遍历，返回 sum[5] = 7。
[1，4] 节点汇总左右两边的结果，得到 9，返回给 [1，8] 节点。
[1，8] 向右遍历，下面流程就不多说了，跟上面 1-5 是一样的，最终右边返回的结果是 18，于是最终结果就是 sum(左) + sum(右) = 18 + 9 = 27。

可以看到上面查询的思路就是从根节点出发，判断当前节点的范围在不在需要查询的结果范围内，然后再继续往左右两侧查询结果，如果发现节点的范围在我们要查询的范围内，直接返回当前下标的总和，比如当遍历到 index = 5 的时候发现 [3，4] 在 [2，7] 之间，于是直接返回 sum[5]，这个 sum[5] 就代表了 index = 3 和 index = 4 的总和，也就是说不需要再遍历 index = 5 左右两个节点。

查询的时间复杂度是 $O (l o g (n))$ ，因为树的高度就是 $O (l o g (n))$ ，在遍历的过程中当遇到节点的范围是要查询的范围之间的就可以直接返回 sum 下标值，加快遍历速度。下面来看下遍历的方法。

// 查询累加和, 比如要查询的范围是 [2, 7]
// jobl: 要查询的区间左边界 2
// jobr: 要查询的区间右边界 7
// l: 当前区间左边界
// r: 当前区间右边界
// i: 当前节点下标
public static long query(int jobl, int jobr, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
// 比如 [3, 4] 在 [2, 7] 之间, 直接返回 sum[i]
return sum[i];
}
int mid = (l + r) >>
1;
down(i, mid - l + 1, r - mid);
long ans = 0;
if (jobl <= mid) {
// 左边查询, 左子节点的下标是当前下标 * 2
ans += query(jobl, jobr, l, mid, i <<
1);
}
if (jobr > mid) {
// 右边查询, 右子节点的下标是当前下标 * 2 + 1, i << 1 | 1 跟 i * 2 + 1 是一样的
ans += query(jobl, jobr, mid + 1, r, i <<
1 | 1);
}
return ans;
}

上面的 down 方法先不管，这个跟线段树的懒更新有关，其他的代码就是求出区间中点，然后分别向左向右遍历查询结果，下面来看下线段树的更新。

2.2 线段树更新

假设现在要设置 [1，4] + 3，[2，6] + 4，也就是原数组 [1，4] 范围的值都 + 3，[2，6] 范围的值都 + 4，那么对于线段树又是怎么维护的呢？首先来看下 [1，4] + 3 这个操作，过程如下图所示。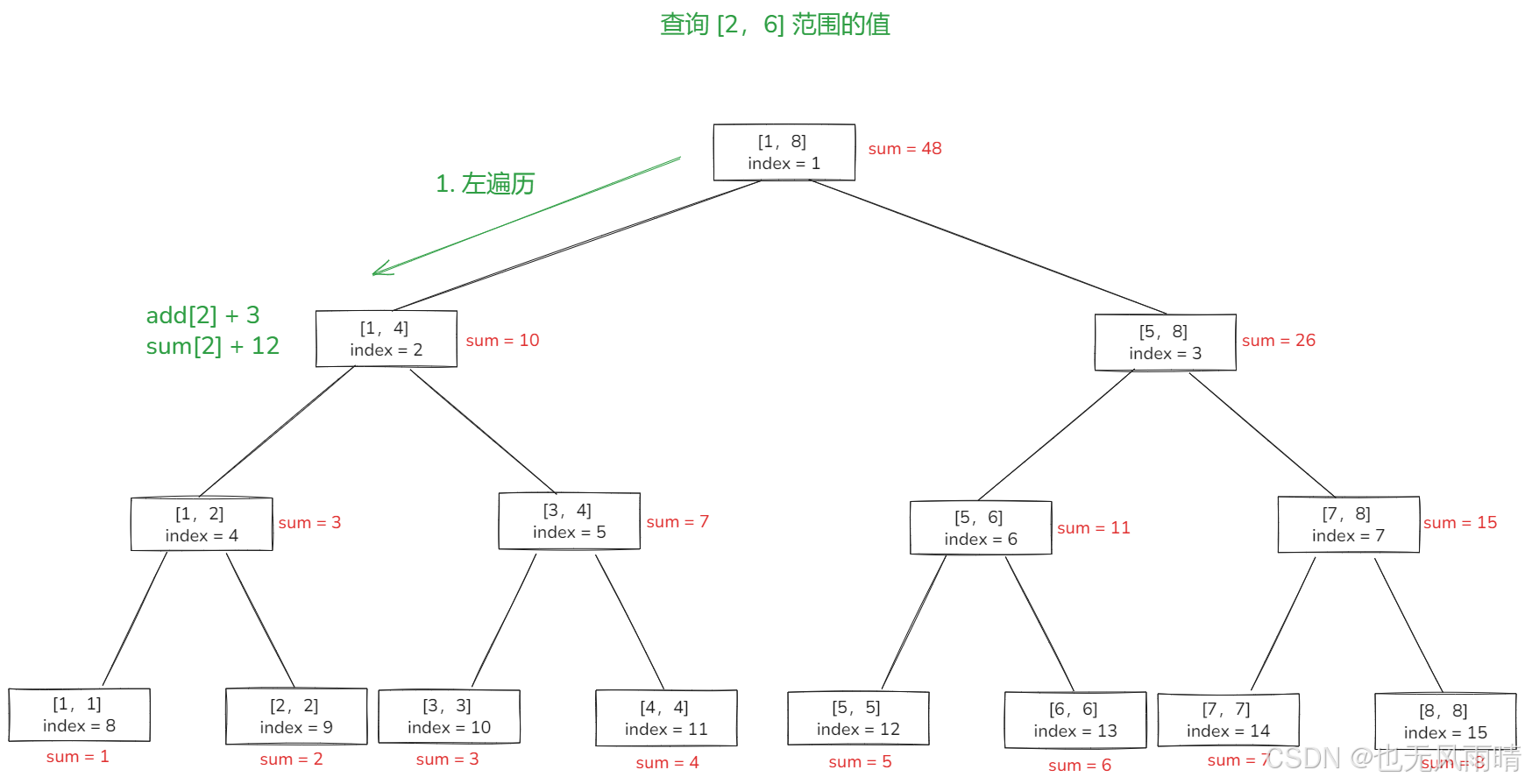

向左遍历，发现 index = 1 的左节点刚好就是 [1，4]，于是设置 add[2] + 3，sum[2] + 12，结束。注意懒更新完之后，index = 1 的值已经变成 48 了，上面忘记画出来了，下面的图你就当 48 去看就行了。当左右节点的值都懒更新完之后，当前节点的 sum 值也会跟着去维护的。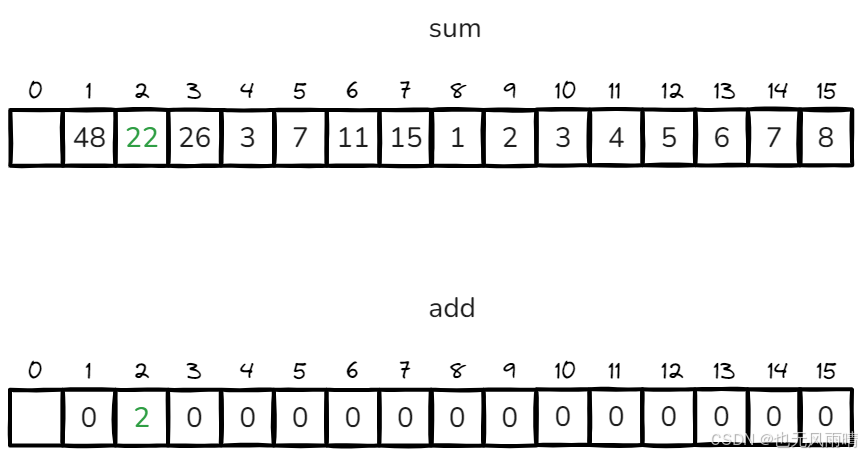

那为什么要这么设置呢？其实就是线段树的 懒更新。所谓懒更新，就是更新的时候我找到了对应的范围，先对这个大范围修改，比如上面要更新 [1，4] + 3，在 index = 1 向左遍历的过程中发现子节点 [1，4] 就刚好是我们要更新的范围，所以直接更新 sum[i] += 12 和 add[i] += 2，然后返回就行了。

假设现在我们要查询 [1，6] 的范围总和，那么大家可以模拟下，其实就是 [1，4] + [5，6] 这两个节点的 sum 值，也就是 sum[2] + sum[6] = 22 + 11 = 33，那现在我要查询 [2，6] 这个范围的总和呢？这就涉及到懒更新的下发了，接着上面的线段树。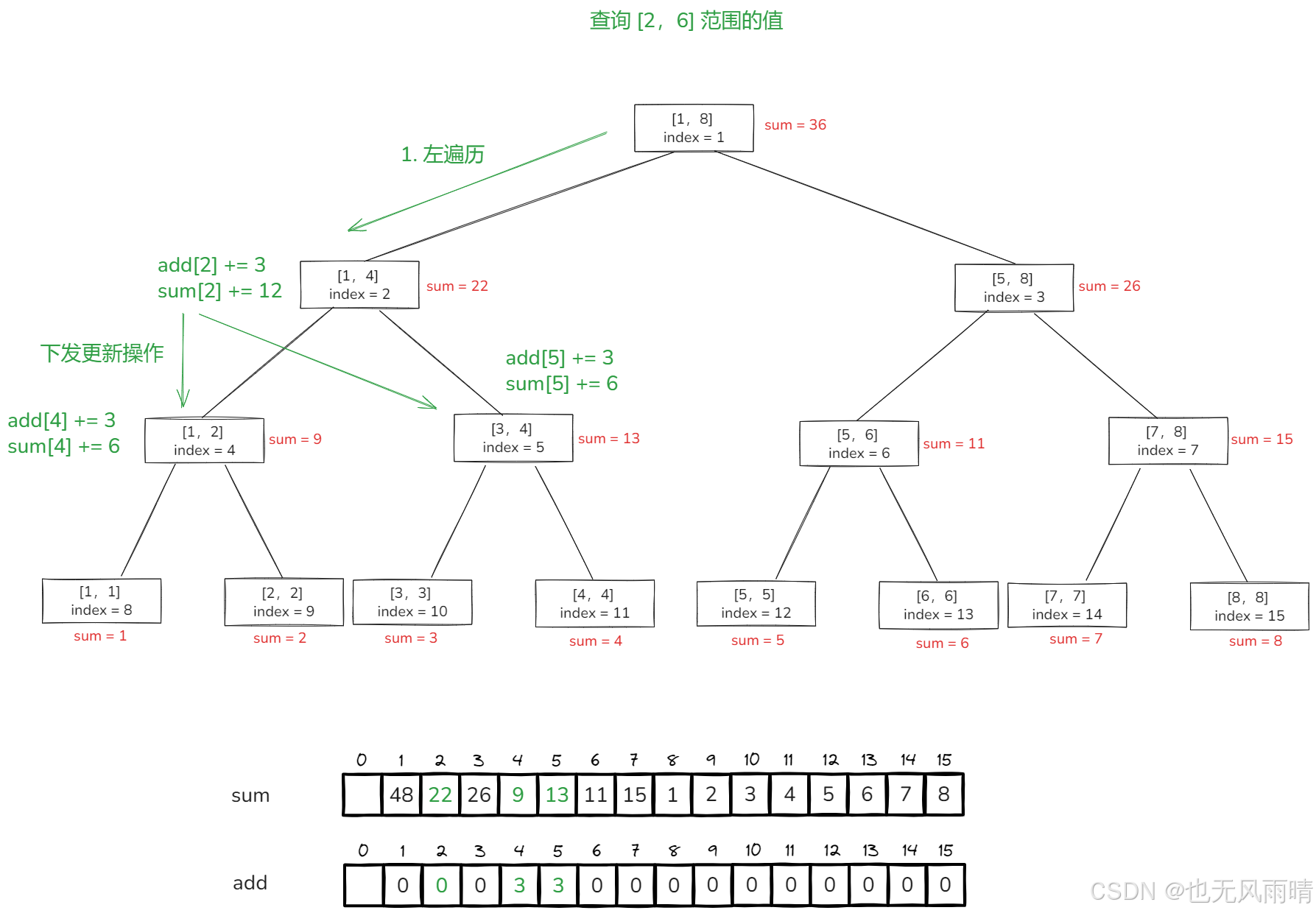

可以看到，当我们向左遍历的时候来到 [1，4] 节点，这个节点还攒着上一次懒添加的操作，这次我们发现要查询的范围 [2，6] 并没有被当前节点包住，这时候需要往 [1，4] 的左右两边递归，那么这种情况下就 下发懒更新操作，也就是说当我们遍历到一个节点之后，发现还得继续往这个节点的左右两个子节点去遍历，这时候才会将这个节点的懒更新下发给子节点，下发的操作也很简单。

add[2 * 2] += 3
sum[2 * 2] += 3 * 2
add[2 * 2 + 1] += 3
sum[2 * 2 + 1] += 3 * 2
add[2] = 0

下发的逻辑也很简单，就是左右两个节点分别更新 add 数组和 sum 数组，最后由于当前节点的 add 已经下发了，设置 add[2] = 0，表示当前节点没用需要懒更新的数据，然后我们接着往下看。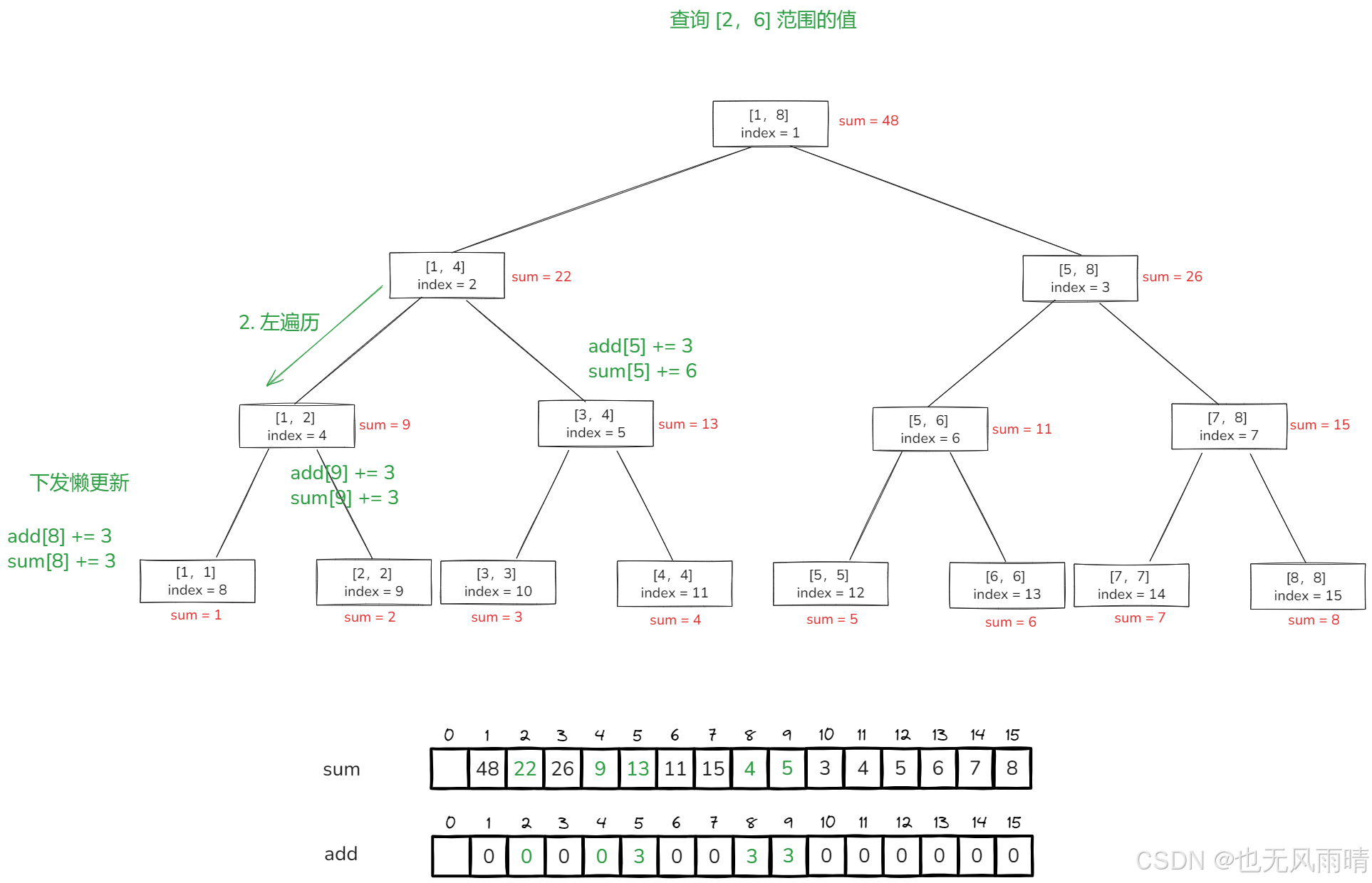

由于 [1，4] 节点还需要向左遍历，来到了 [1，2] 节点，然后发现 [1，2] 也没有被 [2，6] 包住，所以还得继续往右遍历，这时候懒更新 [1，2] 节点上面的值，下发逻辑和上面的一样：

add[4 * 2] += 3
sum[4 * 2] += 3
add[4 * 2 + 1] += 3
sum[4 * 2 + 1] += 3
add[4] = 0

更新完成之后，接着往右遍历，发现 [2，2] 被 [2，6] 包住了，直接返回 sum[9] = 5，一路返回到 [1，4] 节点，这个节点左节点查出来的结果是 5，继续往右遍历。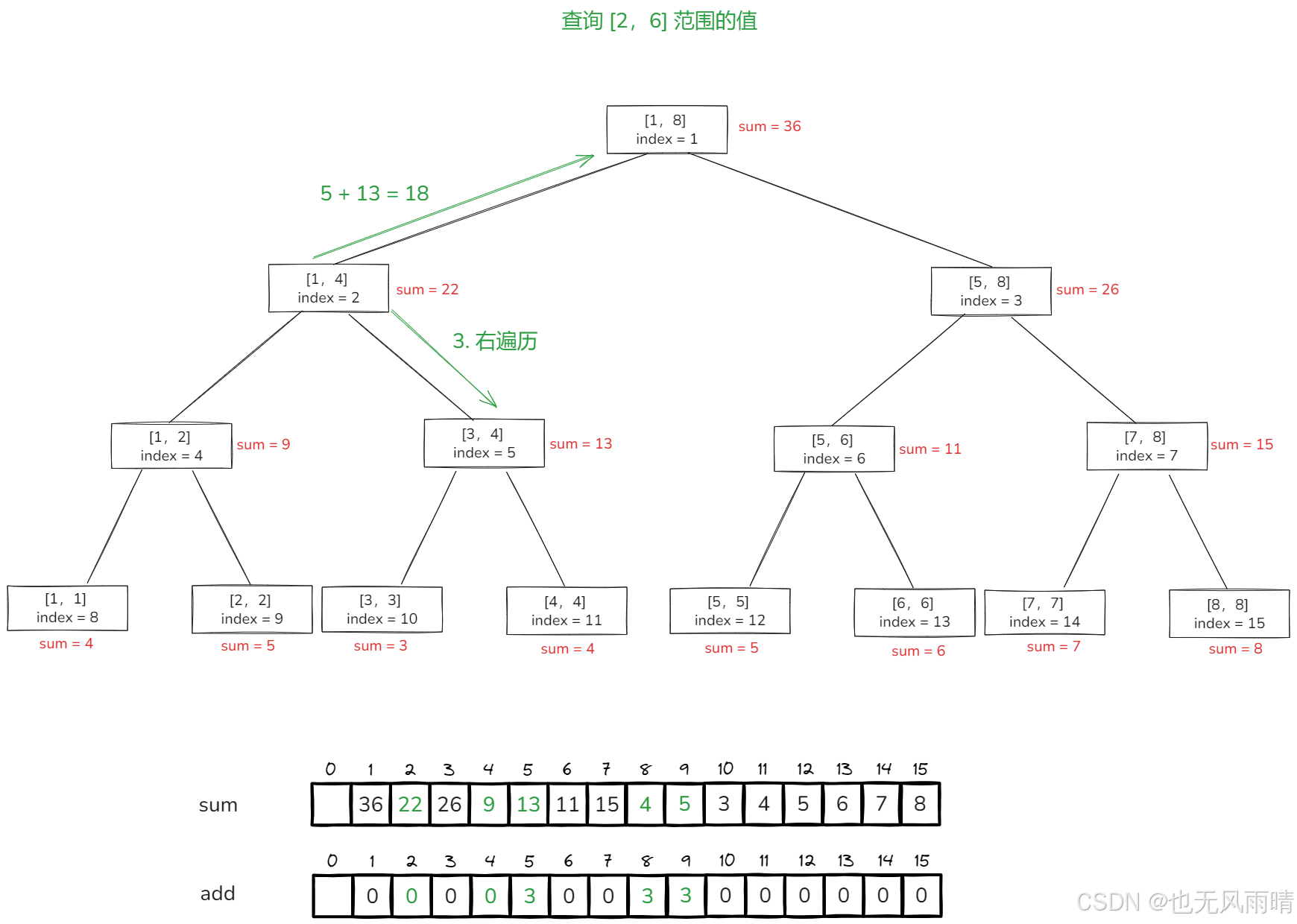

当遍历到 [3，4] 这个节点，发现 [3，4] 被 [2，7] 包住了，这种情况下我们可以直接返回 sum[5] = 13，所以这里就能明确了为什么懒更新下发的时候要更新 sum 数组，因为当查询遍历到某个节点的时候，如果发现这个节点的范围在我们要查询的范围之内，就直接返回 sum 值，而不是来到了这个节点先更新 sum 数组再去判断，所以懒更新下发的时候要把下发的那两个节点维护的总和信息给提前设置好。

接着继续从 [1，8] 节点向右遍历，由于没用涉及到懒更新信息了，所以跟上面查询的流程是一样的，最终右边会返回 11，最终结果就是 18 + 11 = 29。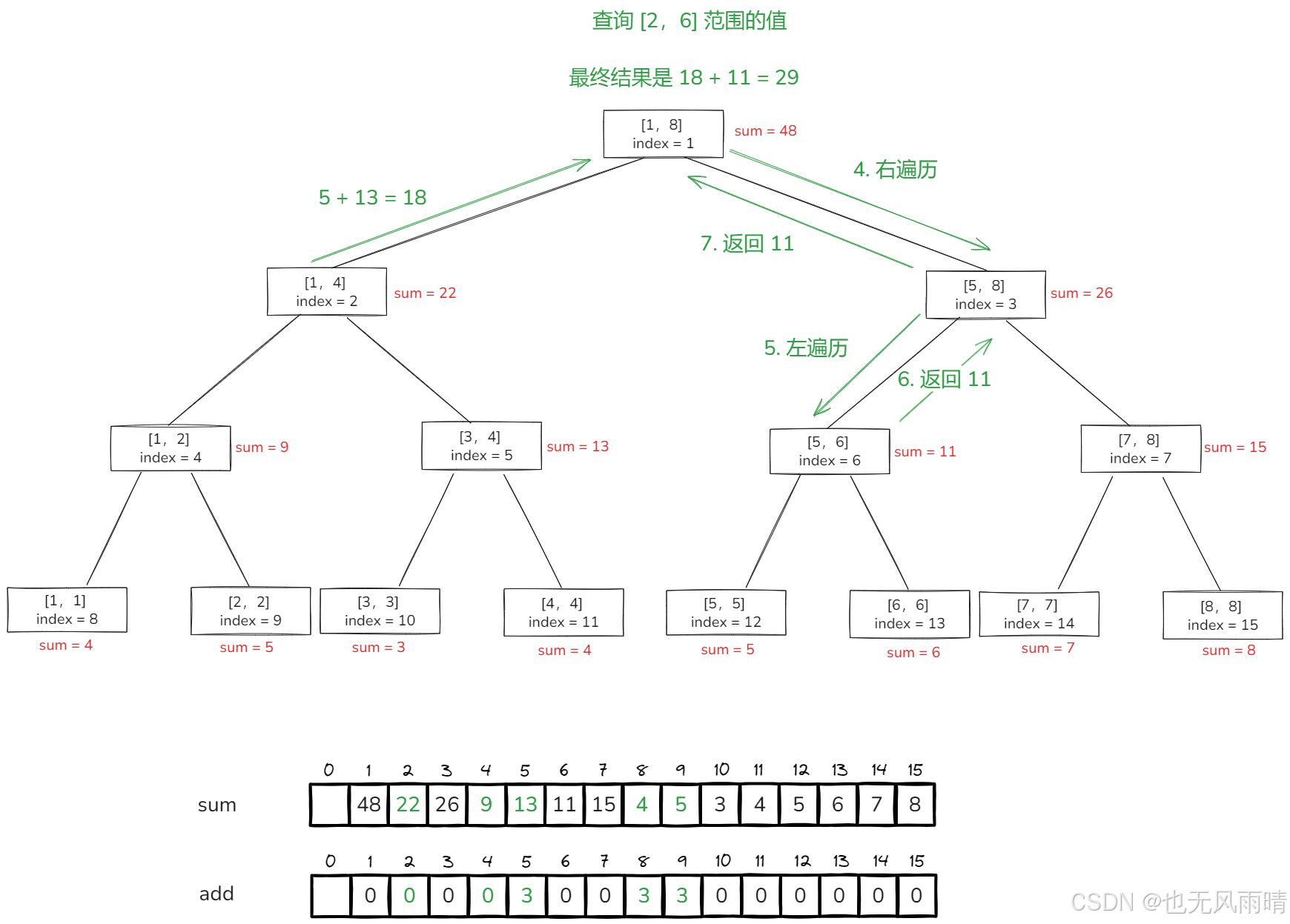

这里就是更新完 [1，4] 了，那下面 [2，6] + 4 的我就不再演示了，大家也可以在看完代码之后用代码去调试，一步一步去看就行了。下面就来看下代码逻辑，首先就是 add。

// 范围修改操作, [jobl, jobr] 范围 + jobv
public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
// 如果当前的下标范围被我们要查询的范围包住了, 直接懒更新
lazy(i, jobv, r - l + 1);
} else {
// 否则左右遍历
int mid = (l + r) >>
1;
// 先把当前节点的懒更新操作给下发下去
down(i, mid - l + 1, r - mid);
if (jobl <= mid) {
// 往左找对应范围更新
add(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
// 往右找对应范围更新
add(jobl, jobr, jobv, mid + 1, r, i <<
1 | 1);
}
// 汇总
up(i);
}
}

下面是 lazy 方法，就是懒更新，当来到 [l，r]，发现这个范围在 [jobl，jobr] 之间，就直接对这个范围的下标 i 懒更新，这个懒更新有可能是第一次到这个范围就把当前线段树的全范围覆盖，也有可能是从父结点下发下来的，总之懒更新的逻辑都是把 sum 和 add 调整好就行。从这里也可以看出，如果范围更新操作使用懒更新可以在 O(1) 时间内完成，那么更新的整体时间复杂度就可以在 O(logn) 时间内完成。

public static void lazy(int i, long v, int n) {
// 这个范围有 n 个数字, 每一个数字需要增加 v, sum 维护就直接加上 n * v
sum[i] += v * n;
// add + v
add[i] += v;
}

因为懒更新就是直接对 sum 和 add 修改，然后这个区间 [l，r] 就算更新完了，所以需要维护的信息在懒更新的时候能够 O(1) 的时间内完成，那么更新就可以一直遍历往根节点走，整体时间复杂度就是树的高度，就是 O(logn)，但是如果懒更新不能在 O(1) 时间内完成，比如那种对范围上的数字求 mod，没办法在 O(1) 时间内完成，这种情况下就需要扫描整棵树了，时间复杂度会来到 O(nlogn)。

还有一点，注意这里更新是 add[i] += v，而不是 add[i] = v，之前写题目总是写错，因为要懒更新的节点可能前面就已经攒了一些懒更新数据了，所以这里是直接叠加上去而不是用等于重置。

// 懒信息的下发
public static void down(int i, int ln, int rn) {
if (add[i] != 0) {
// 下发懒更新信息到左节点
lazy(i <<
1, add[i], ln);
// 下发懒更新信息到右节点
lazy(i <<
1 | 1, add[i], rn);
// 清空父节点的懒更新信息
add[i] = 0;
}
}

上面是懒更新的下发，当前节点下发懒更新信息到左右两个节点，下发之后就清空当前节点的更新信息，避免重复更新。到这里就说完更新和查询了，下面来看题目。

3. 题目

3.1 范围维护累加和

P3372 【模板】线段树 1，这道题是洛谷上面的题目，就是线段树维护区间和，链接：P3372 【模板】线段树 1。

就是上面第二节的代码，下面是完整的代码。

import java.io.*;
public class Main
{
public static int MAXN = 100001;
public static long[] arr = new long[MAXN];
public static long[] sum = new long[MAXN <<
2];
public static long[] add = new long[MAXN <<
2];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
in.nextToken();
int n = (int) in.nval;
in.nextToken();
int m = (int) in.nval;
for (int i = 1; i <= n; i++) {
in.nextToken();
arr[i] = (long) in.nval;
}
build(1, n, 1);
for (int i = 1; i <= m; i++) {
in.nextToken();
int op = (int) in.nval;
if (op == 1) {
in.nextToken();
int jobl = (int) in.nval;
in.nextToken();
int jobr = (int) in.nval;
in.nextToken();
long jobv = (long) in.nval;
add(jobl, jobr, jobv, 1, n, 1);
} else if (op == 2) {
in.nextToken();
int jobl = (int) in.nval;
in.nextToken();
int jobr = (int) in.nval;
out.println(query(jobl, jobr, 1, n, 1));
}
}
out.flush();
out.close();
br.close();
}
public static void build(int l, int r, int i) {
if (l == r) {
sum[i] = arr[l];
} else {
int mid = l + ((r - l) >>
1);
build(l, mid, i <<
1);
build(mid + 1, r, (i <<
1) | 1);
buildSum(i);
}
add[i] = 0;
}
public static void buildSum(int i) {
sum[i] = sum[i <<
1] + sum[(i <<
1) | 1];
}
public static long query(int jobl, int jobr, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
return sum[i];
}
int mid = l + ((r - l) >>
1);
down(i, mid - l + 1, r - mid);
long ans = 0;
if (jobl <= mid) {
ans += query(jobl, jobr, l, mid, i <<
1);
}
if (jobr > mid) {
ans += query(jobl, jobr, mid + 1, r, (i <<
1) | 1);
}
return ans;
}
public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
lazy(i, jobv, r - l + 1);
} else {
int mid = l + ((r - l) >>
1);
down(i, mid - l + 1, r - mid);
if (jobl <= mid) {
add(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
add(jobl, jobr, jobv, mid + 1, r, (i <<
1) | 1);
}
buildSum(i);
}
}
private static void down(int i, int ln, int rn) {
if (add[i] != 0) {
lazy(i <<
1, add[i], ln);
lazy((i <<
1) | 1, add[i], rn);
add[i] = 0;
}
}
private static void lazy(int i, long v, int cnt) {
add[i] += v;
sum[i] += v * cnt;
}
}

3.2 范围增加维护最大值

上面是线段树范围增加维护累加和，这里是范围增加维护最大值，原理都是一样的，需要关注的就是 down 方法和 lazy 方法，也就是如何维护最大值，懒更新如何下发。

首先是最大值懒更新，假设当前数组还是 [1，2，3，4，5，6，7，8]，构建出来的线段树如下：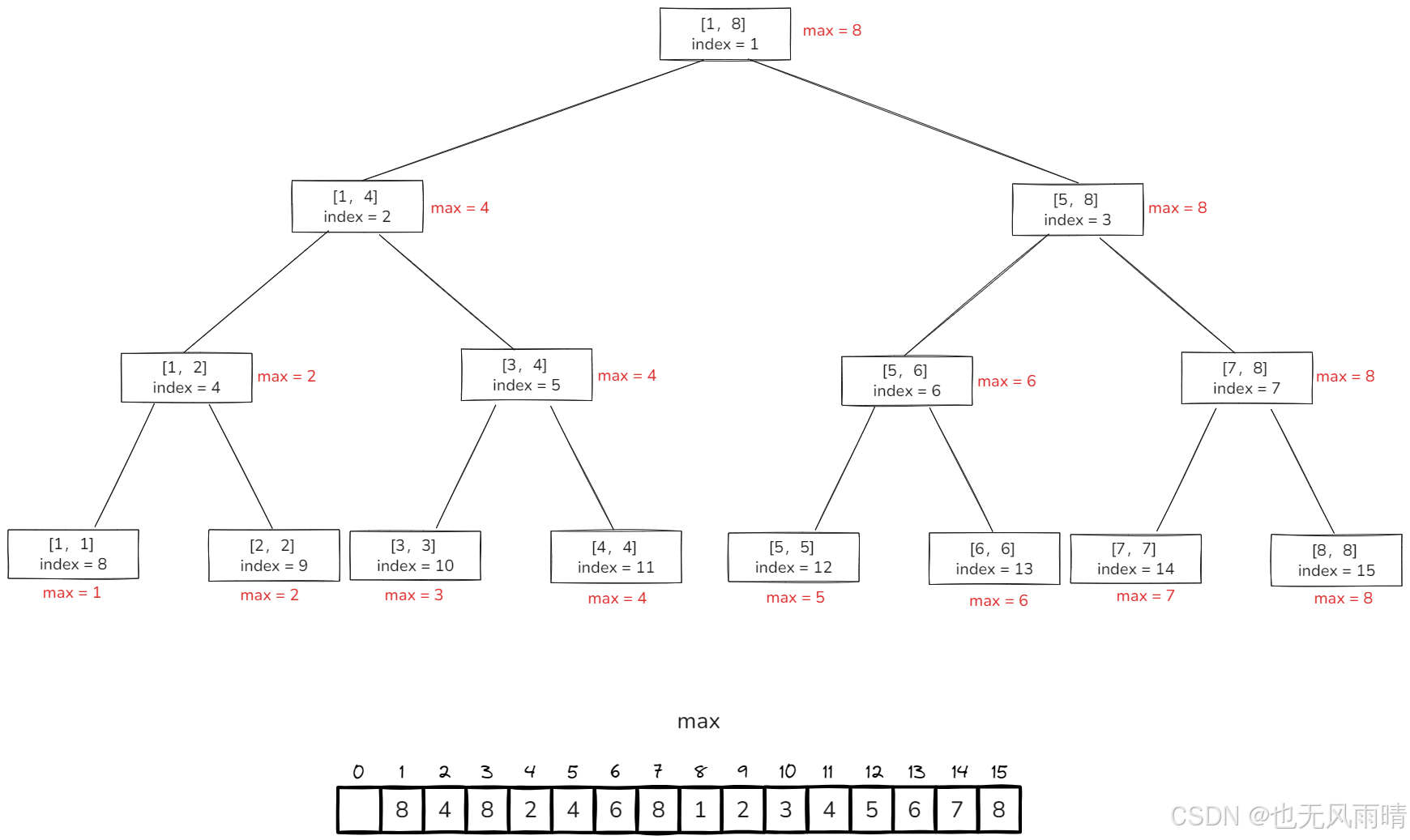

好了，然后我们来看下懒更新，假设现在需要在 [1，4] 范围 + 4，懒更新之后结果如下：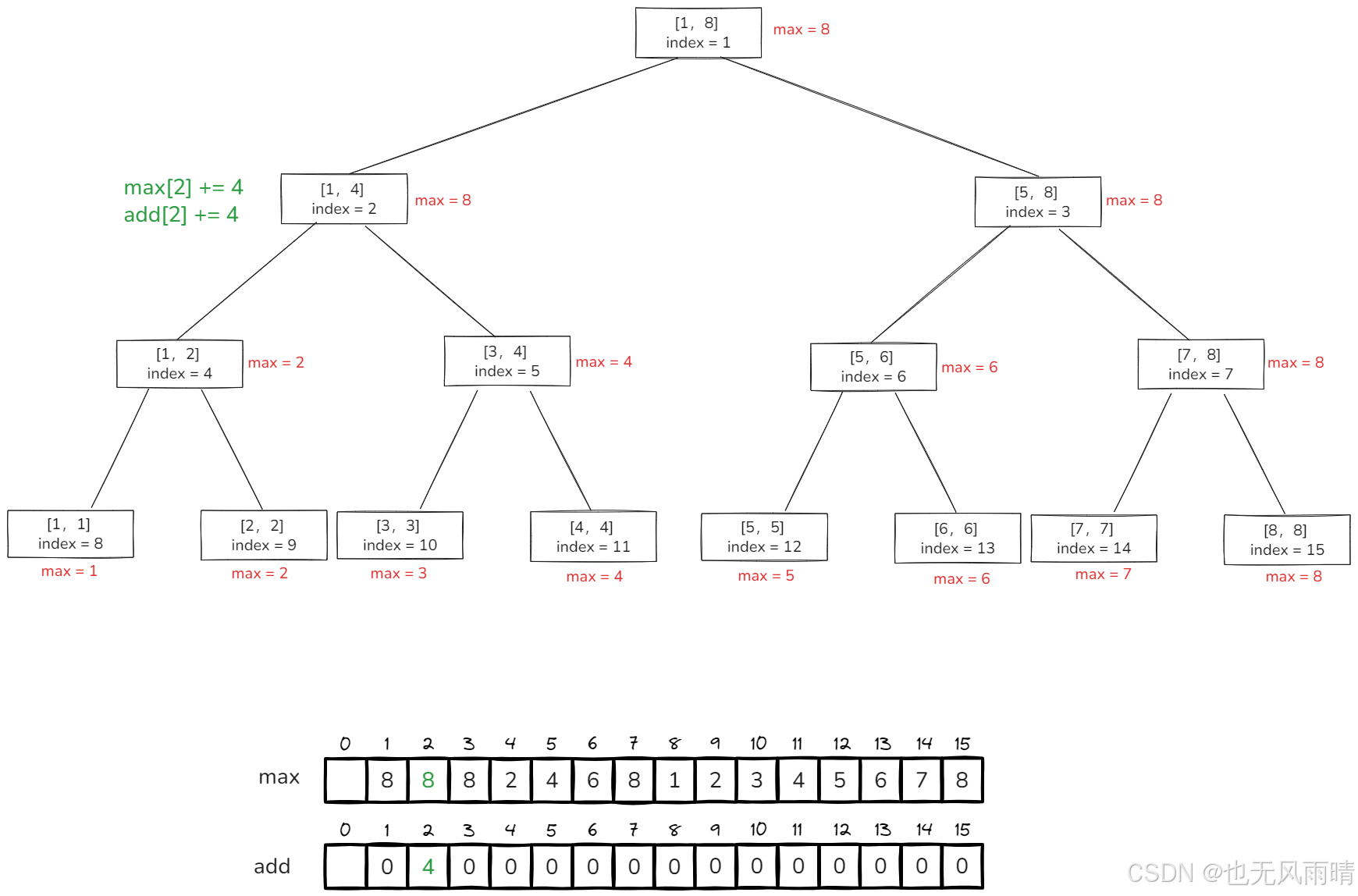

可以看到最大值的懒更新维护还是一样，更新 add 数组和 max 数组就行，假设当前 [1，4] 范围最大值是 4，那么现在需要在 [1，4] 范围 + 4，最大值自然是 8 了。

那么当懒更新下发的时候，子节点能不能在 O(1) 时间内更新完呢？也就是 down 方法能不能在 O(1) 时间内弄完，当然是可以的，同样的，子节点下发的时候：

max[4] += 4
add[4] += 4
max[5] += 4
add[5] += 4
add[2] = 0

做完这几步就没问题了，子节点的更新也是直接加上 v，不需要加上 v * n (子节点范围的数字个数)，因为最大值不像 sum，sum 要求总和，下发当然要用节点个数 * 下发的值，但是最大值只需要看某一个节点的最大值就行。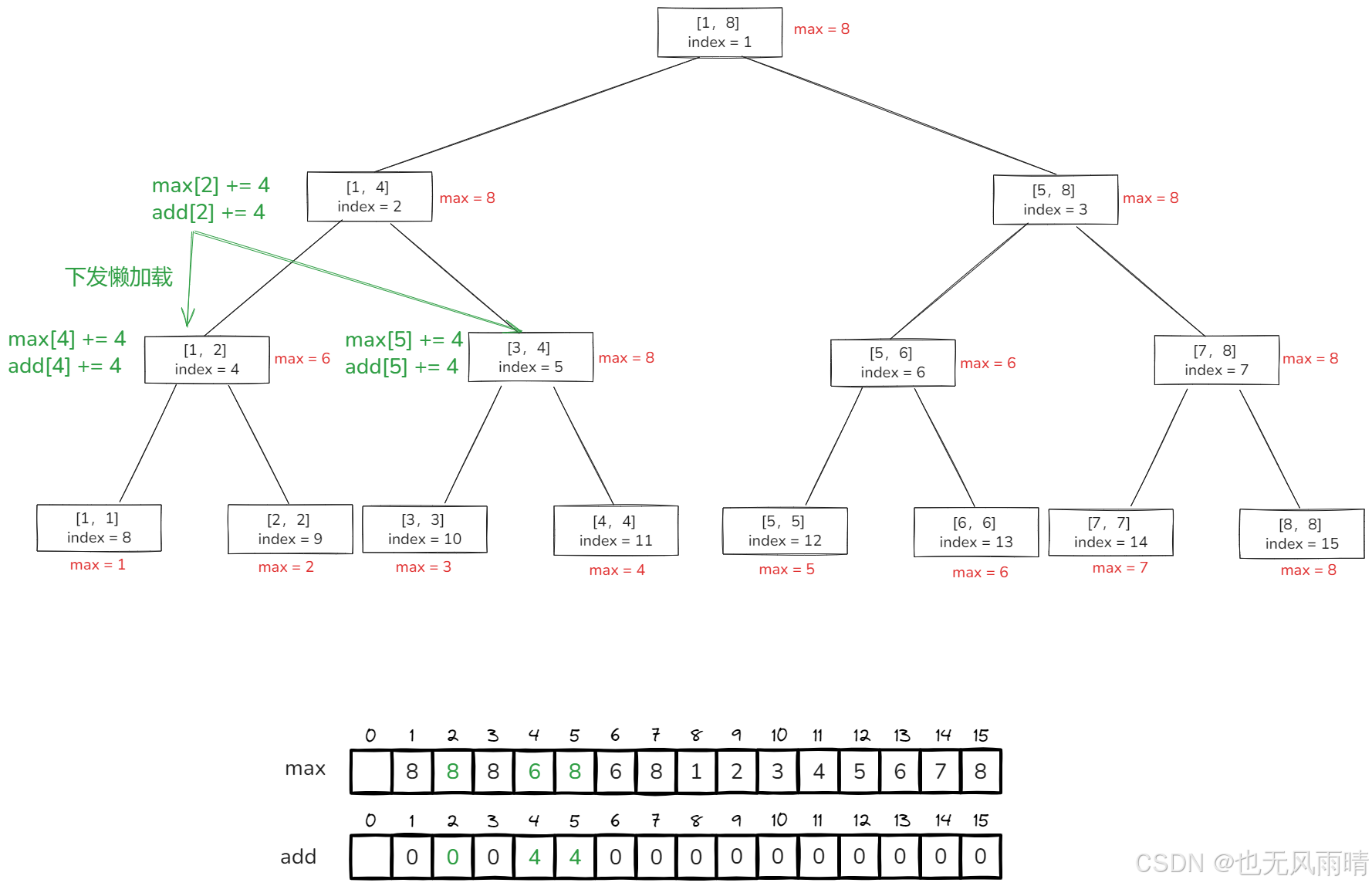

好了，上面就是懒加载和下发的流程了，然后我们来看下下发的代码。

public static void down(int i) {
if (add[i] != 0) {
lazy(i <<
1, add[i]);
lazy(i <<
1 | 1, add[i]);
add[i] = 0;
}
}
public static void lazy(int i, long v) {
max[i] += v;
add[i] += v;
}

由于不需要传入节点个数，所以 down 方法只需要传入当前下标就行，而懒更新子节点的也是直接加上 add[i] 的值即可，下面来看下全部的代码。

public class Main
{
public static int MAXN = 100001;
// 原数组
public static long[] arr = new long[MAXN];
// 线段树, 维护最大值
public static long[] max = new long[MAXN <<
2];
// 线段树的懒更新数组
public static long[] add = new long[MAXN <<
2];
// 当懒更新完左右节点之后维护当前节点最大值
public static void up(int i) {
max[i] = Math.max(max[i <<
1], max[i <<
1 | 1]);
}
// 下发懒加载
public static void down(int i) {
if (add[i] != 0) {
// 下发懒更新信息到左边
lazy(i <<
1, add[i]);
// 下发懒更新信息到右边
lazy(i <<
1 | 1, add[i]);
// 清空父结点的懒更新信息
add[i] = 0;
}
}
// 懒更新
public static void lazy(int i, long v) {
// 维护最大值
max[i] += v;
// 维护懒更新信息
add[i] += v;
}
public static void build(int l, int r, int i) {
if (l == r) {
max[i] = arr[l];
} else {
int mid = (l + r) >>
1;
build(l, mid, i <<
1);
build(mid + 1, r, i <<
1 | 1);
up(i);
}
add[i] = 0;
}
public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
lazy(i, jobv);
} else {
// 下发懒更新信息
down(i);
int mid = (l + r) >>
1;
if (jobl <= mid) {
add(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
add(jobl, jobr, jobv, mid + 1, r, i <<
1 | 1);
}
// 更新完左右节点，更新当前节点的 max 信息
up(i);
}
}
public static long query(int jobl, int jobr, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
return max[i];
}
// 下发当前的懒更新信息
down(i);
int mid = (l + r) >>
1;
long ans = Long.MIN_VALUE;
if (jobl <= mid) {
ans = Math.max(ans, query(jobl, jobr, l, mid, i <<
1));
}
if (jobr > mid) {
ans = Math.max(ans, query(jobl, jobr, mid + 1, r, i <<
1 | 1));
}
return ans;
}
}

这里要注意下就是 query 方法是不需要使用 up 方法的，因为 query 方法没用更新节点信息，只是把节点的懒更新下发下去，而下发懒更新的时候 max 数组和 add 数组就维护好了，根本不需要再 up 维护当前节点的最大值。

3.3 范围重置维护累加和

再来看下范围重置维护累加和，范围重置的意思就是 [L，R] 区间的数字都修改成数字 v，来看下这个线段树要怎么维护。

首先累加和还是使用 sum 数组来维护，然后范围重置我们可以用两个数组，分别是 change 和 update 来表示。

public static long[] change = new long[MAXN <<
2];
public static boolean[] update = new boolean[MAXN <<
2];

change[i] 表示这个范围的数字要重置成什么数，update[i] 表示这个范围的数字是否需要重置，为什么不用一个 change 数组来表示呢，只要 change[i] 不为 0 就代表需要重置，但是这种情况前面也说了 change[i] 不为 0 代表需要重置，如果为 0，不确定是需要重置为 0 还是不需要重置，所以另外使用一个数组 update 来表示是否需要重置。

然后再来看下范围重置的懒下发，由于重置代表 [l，r] 这个范围的数字都重置成了 v，那么懒更新的时候我们就设置 update[i] = true，change[i] = v，sum[i] = v * n。

public static void lazy(int i, long v, int n) {
// 范围总和变成了 v * n, v 是重置的数字, n 是这个范围的数字个数
sum[i] = v * n;
// 重置为 v
change[i] = v;
// 需要更新
update[i] = true;
}

下发操作的时候同样的判断 update[i] 是否为 false，如果是就不下发，如果不是就说明有重置操作，下发给子节点。

public static void down(int i, int ln, int rn) {
if (update[i]) {
// 下发左子节点
lazy(i <<
1, change[i], ln);
// 下发右子节点
lazy(i <<
1 | 1, change[i], rn);
// 重置当前节点
update[i] = false;
}
}

大家可以看到这里下发完成之后是不需要更新 change 数组的，因为下发只看 update，就算 change 不设置，update = false 也不会下发下去，而当 update[i] = true 的时候 change[i] 肯定就是我们要下发的值，所以不需要维护 change 数组，下面来看下所有代码。

public class Main
{
public static int MAXN = 100001;
public static long[] arr = new long[MAXN];
// 维护区间总和信息
public static long[] sum = new long[MAXN <<
2];
// 懒更新的值
public static long[] change = new long[MAXN <<
2];
// 是否需要懒更新
public static boolean[] update = new boolean[MAXN <<
2];
public static void up(int i) {
sum[i] = sum[i <<
1] + sum[i <<
1 | 1];
}
public static void down(int i, int ln, int rn) {
if (update[i]) {
// 下发左子节点
lazy(i <<
1, change[i], ln);
// 下发右子节点
lazy(i <<
1 | 1, change[i], rn);
// 重置当前节点
update[i] = false;
}
}
public static void lazy(int i, long v, int n) {
// 范围总和变成了 v * n, v 是重置的数字, n 是这个范围的数字个数
sum[i] = v * n;
// 重置为 v
change[i] = v;
// 需要更新
update[i] = true;
}
public static void build(int l, int r, int i) {
if (l == r) {
sum[i] = arr[l];
} else {
int mid = (l + r) >>
1;
build(l, mid, i <<
1);
build(mid + 1, r, i <<
1 | 1);
up(i);
}
change[i] = 0;
update[i] = false;
}
public static void update(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
// 懒更新
lazy(i, jobv, r - l + 1);
} else {
// 中点
int mid = (l + r) >>
1;
// 下发当前的懒更新操作
down(i, mid - l + 1, r - mid);
if (jobl <= mid) {
// 往左节点更新
update(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
// 往右节点更新
update(jobl, jobr, jobv, mid + 1, r, i <<
1 | 1);
}
// 维护当前节点的值
up(i);
}
}
public static long query(int jobl, int jobr, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
return sum[i];
}
int mid = (l + r) >>
1;
// 下发懒更新的重置操作
down(i, mid - l + 1, r - mid);
long ans = 0;
if (jobl <= mid) {
// 查询左
ans += query(jobl, jobr, l, mid, i <<
1);
}
if (jobr > mid) {
// 查询右
ans += query(jobl, jobr, mid + 1, r, i <<
1 | 1);
}
return ans;
}
}

3.4 范围重置维护最大值

这个跟上面 3.3 是一样的，只是换成了维护最大值，只需要修改下 up 操作就行了。

public class Main
{
public static int MAXN = 100001;
// 原数组
public static long[] arr = new long[MAXN];
// 线段树维护最大值
public static long[] max = new long[MAXN <<
2];
// 区间重置懒更新数组
public static long[] change = new long[MAXN <<
2];
// 区间重置是否需要懒更新
public static boolean[] update = new boolean[MAXN <<
2];
// 维护最大值
public static void up(int i) {
max[i] = Math.max(max[i <<
1], max[i <<
1 | 1]);
}
// 下发懒更新操作
public static void down(int i) {
if (update[i]) {
lazy(i <<
1, change[i]);
lazy(i <<
1 | 1, change[i]);
update[i] = false;
}
}
public static void lazy(int i, long v) {
max[i] = v;
change[i] = v;
update[i] = true;
}
public static void build(int l, int r, int i) {
if (l == r) {
max[i] = arr[l];
} else {
int mid = (l + r) >>
1;
build(l, mid, i <<
1);
build(mid + 1, r, i <<
1 | 1);
up(i);
}
change[i] = 0;
update[i] = false;
}
public static void update(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
// 懒更新
lazy(i, jobv);
} else {
// 下发懒更新
down(i);
int mid = (l + r) >>
1;
if (jobl <= mid) {
update(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
update(jobl, jobr, jobv, mid + 1, r, i <<
1 | 1);
}
// 维护当前下标的值
up(i);
}
}
public static long query(int jobl, int jobr, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
return max[i];
}
// 下发懒更新操作
down(i);
int mid = (l + r) >>
1;
// 求最大值
long ans = Long.MIN_VALUE;
if (jobl <= mid) {
ans = Math.max(ans, query(jobl, jobr, l, mid, i <<
1));
}
if (jobr > mid) {
ans = Math.max(ans, query(jobl, jobr, mid + 1, r, i <<
1 | 1));
}
return ans;
}
}

3.5 范围重置、范围增加维护累加和

这一小节我们再来看下范围重置、范围增加维护累加和要怎么写。由于一个区间上既可以添加，又可以重置，所以下发的时候前后顺序就比较重要了，首先来明确下懒重置和懒新增的逻辑。

// 懒重置操作
public static void updateLazy(int i, long v, int n) {
// 维护 sum 数组
sum[i] = v * n;
// 由于区间重置, 之前攒的区间增加也重置为 0
add[i] = 0;
update[i] = true;
change[i] = v;
}
// 懒新增
public static void addLazy(int i, long v, int n) {
sum[i] += v * n;
add[i] += v;
}

懒重置就是将这个区间内的数字全部重置为 v，既然重置了，那么之前攒下来的懒更新 add[i] 也得重置，不需要再往下发了。而懒新增就是更新 sum 数组和 add 数组，跟原来的是一样的。

那么 down 下发要怎么处理呢？假设一个节点 update[i] = true，同时 add[i] > 0，是先下发 update 还是先下发 add 呢? 先下发 update 再下发 add。

为什么呢？假设现在有三个操作：[1，4] 范围内区间新增 2，[1，4] 范围内区间重置为 1，[1，4] 范围内区间新增 3，下面先看下 [1，4] 范围新增 2。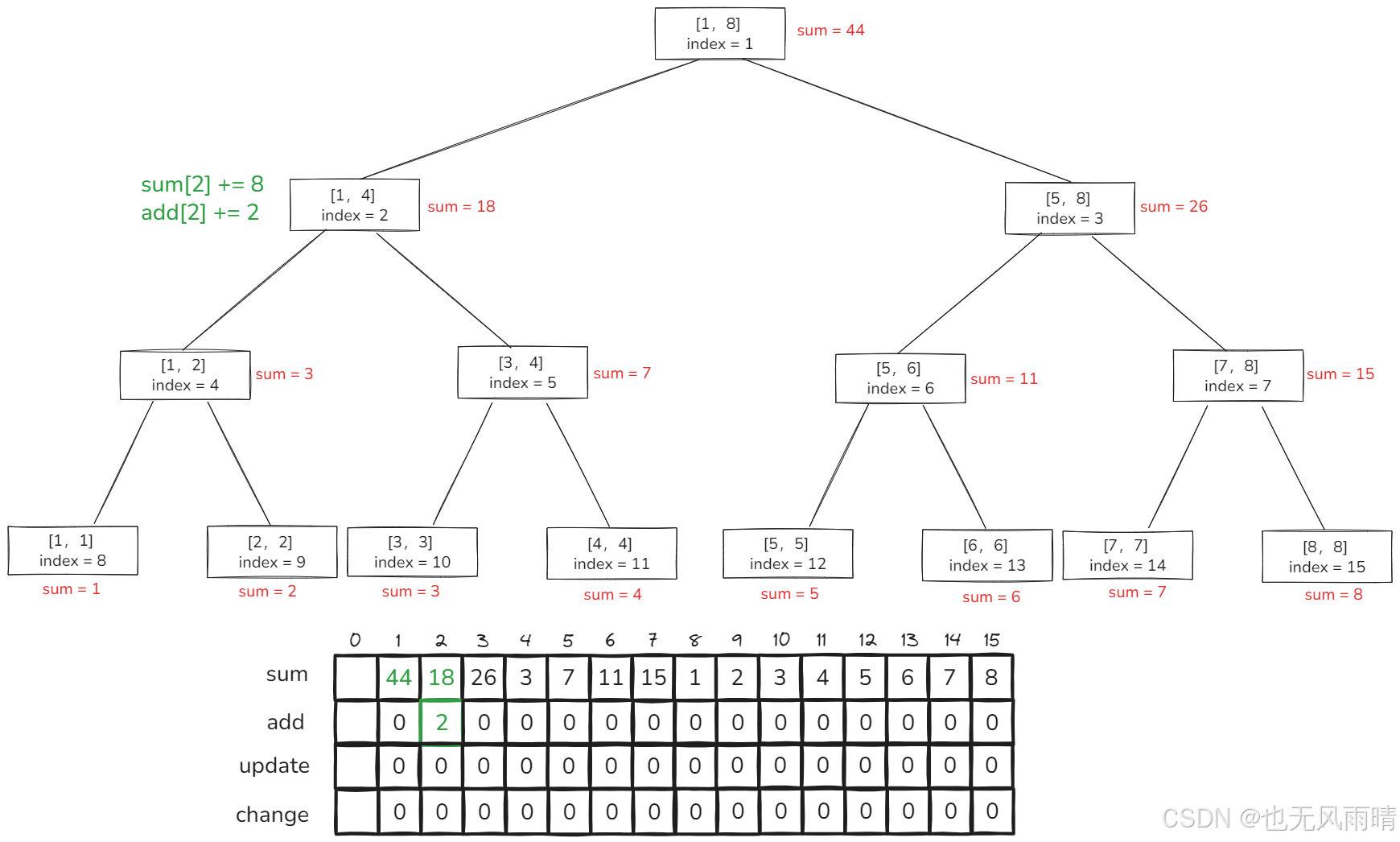

然后再来看下 [1，4] 范围内区间重置为 1，重置结果如下。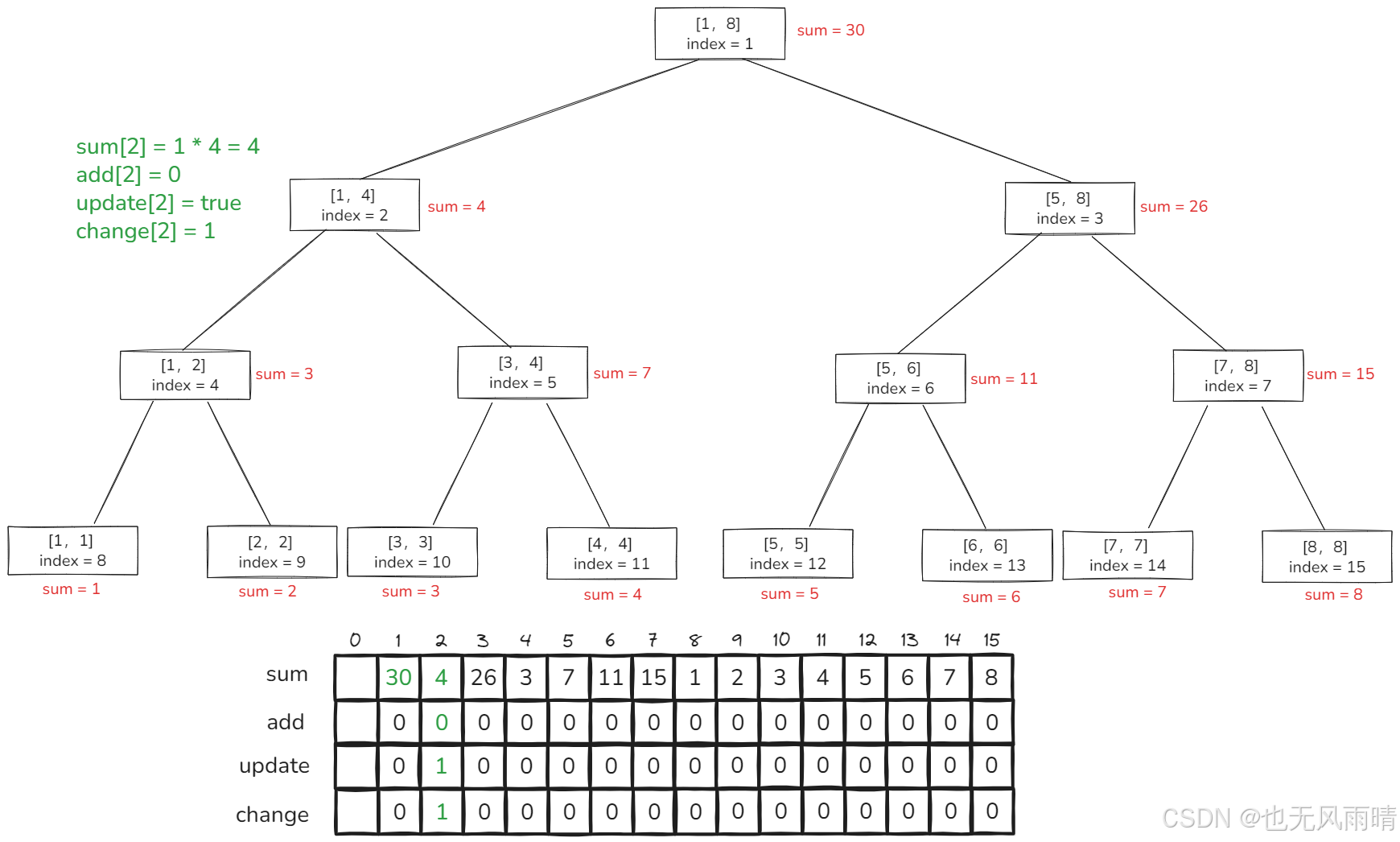

然后再设置 [1，4] 范围内区间新增 3，结果如下：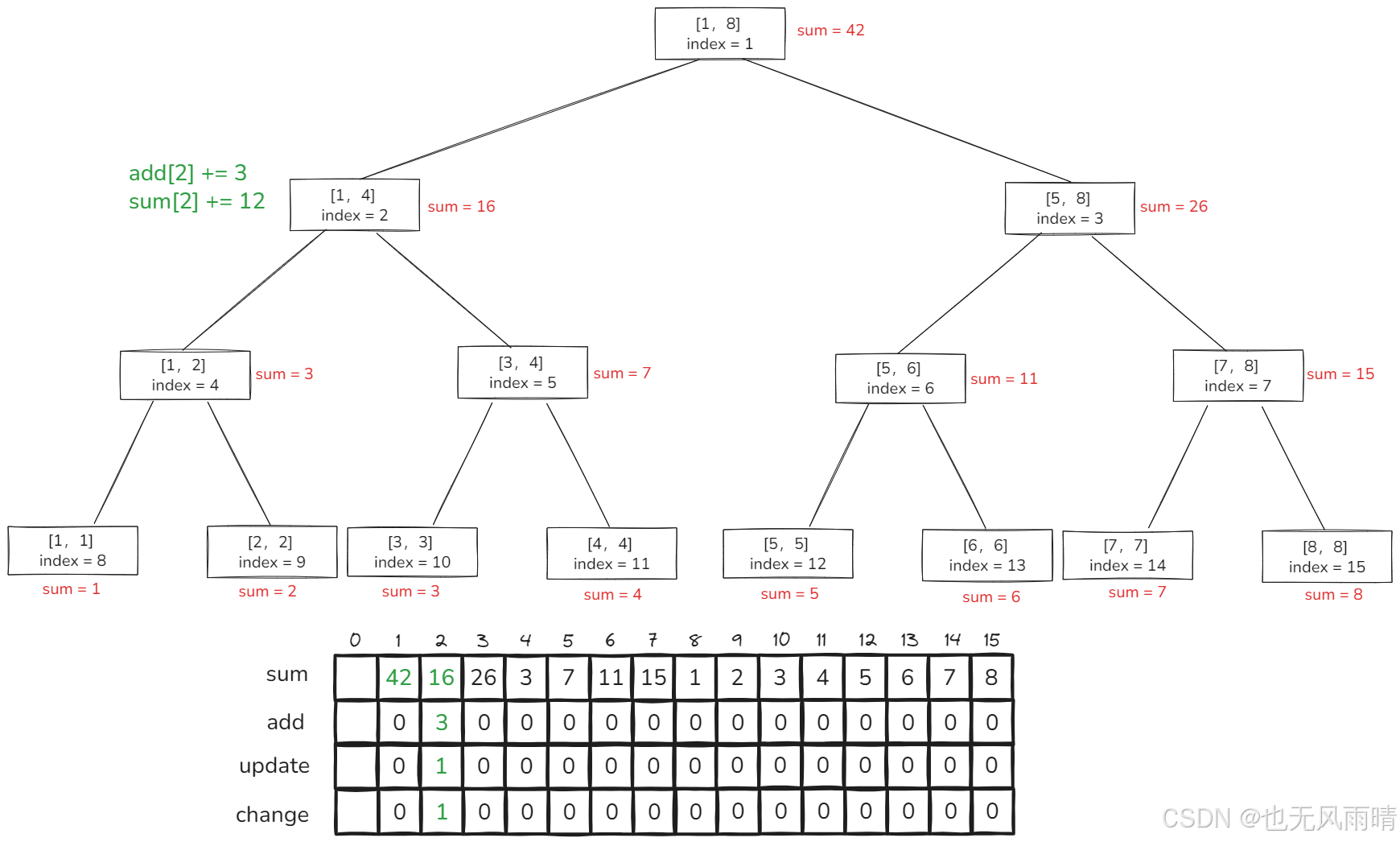

好了，这时候我们可以看到，现在下标 2 上面既有重置为 1 的操作，又有新增 3 的操作需要下发，假设这时候来了一个查询 [1，2] 的逻辑，要下发这两个操作，我们知道由于上面的几个操作中最后的操作是 add，所以先下发 [1，2] 重置为 1，再下发 [1，2] 区间内 + 3 的更新，最终结果就没有问题。

那如果是最后的操作是 update 呢？是不是就先下发 add，再下发 update 了？并不是，因为 update 重置会把 add 更新为 0，所以这种情况下还是先下发 update，由于 add[i] 被 update[i] 重置为 0 了，所以并不会下发 add，因此我们的下发逻辑就是先重置再 add。总之就是由于 update 会影响 add，所以先把 update 发了，然后再判断 add 还需不需要发。

// 下发懒更新
public static void down(int i, int ln, int rn) {
// 先维护重置操作
if (update[i]) {
updateLazy(i <<
1, change[i], ln);
updateLazy(i <<
1 | 1, change[i], rn);
update[i] = false;
}
// 再维护新增操作
if (add[i] != 0) {
addLazy(i <<
1, add[i], ln);
addLazy(i <<
1 | 1, add[i], rn);
add[i] = 0;
}
}

既然这两个最大的问题都解决了，下面就来看下全部代码。

public class Main
{
public static int MAXN = 1000001;
// 原数组
public static long[] arr = new long[MAXN];
// 线段树维护累加和
public static long[] sum = new long[MAXN <<
2];
// 懒更新维护区间累加和
public static long[] add = new long[MAXN <<
2];
// 懒更新维护区间重置
public static long[] change = new long[MAXN <<
2];
public static boolean[] update = new boolean[MAXN <<
2];
public static void up(int i) {
sum[i] = sum[i <<
1] + sum[i <<
1 | 1];
}
// 下发懒更新
public static void down(int i, int ln, int rn) {
// 先维护重置操作
if (update[i]) {
updateLazy(i <<
1, change[i], ln);
updateLazy(i <<
1 | 1, change[i], rn);
update[i] = false;
}
// 再维护新增操作
if (add[i] != 0) {
addLazy(i <<
1, add[i], ln);
addLazy(i <<
1 | 1, add[i], rn);
add[i] = 0;
}
}
// 懒重置操作
public static void updateLazy(int i, long v, int n) {
// 维护 sum 数组
sum[i] = v * n;
// 由于区间重置, 之前攒的区间增加也重置为 0
add[i] = 0;
update[i] = true;
change[i] = v;
}
// 懒新增
public static void addLazy(int i, long v, int n) {
sum[i] += v * n;
add[i] += v;
}
public static void build(int l, int r, int i) {
if (l == r) {
sum[i] = arr[l];
} else {
int mid = (l + r) >>
1;
build(l, mid, i <<
1);
build(mid + 1, r, i <<
1 | 1);
up(i);
}
add[i] = 0;
change[i] = 0;
update[i] = false;
}
public static void update(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
// 懒更新
updateLazy(i, jobv, r - l + 1);
} else {
int mid = (l + r) >>
1;
down(i, mid - l + 1, r - mid);
if (jobl <= mid) {
update(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
update(jobl, jobr, jobv, mid + 1, r, i <<
1 | 1);
}
up(i);
}
}
public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
// 懒新增
addLazy(i, jobv, r - l + 1);
} else {
int mid = (l + r) >>
1;
down(i, mid - l + 1, r - mid);
if (jobl <= mid) {
add(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
add(jobl, jobr, jobv, mid + 1, r, i <<
1 | 1);
}
up(i);
}
}
public static long query(int jobl, int jobr, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
return sum[i];
}
int mid = (l + r) >>
1;
down(i, mid - l + 1, r - mid);
long ans = 0;
if (jobl <= mid) {
ans += query(jobl, jobr, l, mid, i <<
1);
}
if (jobr > mid) {
ans += query(jobl, jobr, mid + 1, r, i <<
1 | 1);
}
return ans;
}
}

3.6 范围重置、范围增加维护最大值

题目来源：P1253 扶苏的问题。

下面给出代码，跟上面 3.5 差不多，只是把 up 方法改成了维护最大值。

3.7 范围乘积，维护累加和

题目：P3373 【模板】线段树 2。

既然要维护区间乘积和累加和，还是上面 3.5 节提出来的问题，就是当一个区间所有数字都 * k 的时候，能不能立刻就维护好这个区间的累加和。

答案是肯定可以的，比如这个区间 sum[i] = (a[i] + a[2] + ... + a[n]) ，当每个数字 * k 的时候就是 (a[i] + a[2] + ... + a[n]) * k，所以我们维护 lazyMulti 的时候 sum 数组就直接改成 sum[i] * k 就行，然后再来看下下发的时候先下发相乘的懒操作还是新增的懒操作。假设现在来到一个节点 i，这个节点上面有一个 add[i] 的懒操作还没有发下去，现在要将这个节点的范围 * k，那么这时候 add[i] 也应该 * k，因为 add[i] 发下去之后，这个区间再乘 k，累加和就变成了 (a[1] + add[i]) * k + (a[2] + add[i]) * k + ... + (a[n] + add[i]) * k，其实就相当于 (a[1] + a[2] + ... + a[n]) * k + n * k * add[i]，所以下发乘法的时候对于 add，同样需要 * k，这样下发下去，加起来才会是 n * k * add[i]，n 是指这个区间有多少个节点。

整体代码就如下，由于最后需要对 m 取模，可以把 m 分到下发的每一步，防止用 long 最后再统一取模溢出。

import java.io.*;
public class Main
{
public static int MAXN = 100001;
public static long[] arr = new long[MAXN];
public static long[] sum = new long[MAXN <<
2];
public static long[] mul = new long[MAXN <<
2];
public static long[] add = new long[MAXN <<
2];
public static int n, q, m = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
in.nextToken();
n = (int) in.nval;
in.nextToken();
q = (int) in.nval;
in.nextToken();
m = (int) in.nval;
for (int i = 1; i <= n; i++) {
in.nextToken();
arr[i] = (long) in.nval;
}
build(1, n, 1);
for (int i = 1; i <= q; i++) {
in.nextToken();
int op = (int) in.nval;
if (op == 1) {
in.nextToken();
int jobl = (int) in.nval;
in.nextToken();
int jobr = (int) in.nval;
in.nextToken();
long jobv = (long) in.nval;
mul(jobl, jobr, jobv, 1, n, 1);
} else if (op == 2) {
in.nextToken();
int jobl = (int) in.nval;
in.nextToken();
int jobr = (int) in.nval;
in.nextToken();
long jobv = (long) in.nval;
add(jobl, jobr, jobv, 1, n, 1);
} else if (op == 3) {
in.nextToken();
int jobl = (int) in.nval;
in.nextToken();
int jobr = (int) in.nval;
out.println(query(jobl, jobr, 1, n, 1));
}
}
out.flush();
out.close();
br.close();
}
private static void mul(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
lazyMulti(i, jobv);
} else {
int mid = l + ((r - l) >>
1);
down(i, mid - l + 1, r - mid);
if (jobl <= mid) {
mul(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
mul(jobl, jobr, jobv, mid + 1, r, (i <<
1) | 1);
}
buildSum(i);
}
}
public static void build(int l, int r, int i) {
if (l == r) {
sum[i] = arr[l];
} else {
int mid = l + ((r - l) >>
1);
build(l, mid, i <<
1);
build(mid + 1, r, (i <<
1) | 1);
buildSum(i);
}
add[i] = 0;
mul[i] = 1L;
}
public static void buildSum(int i) {
sum[i] = sum[i <<
1] + sum[(i <<
1) | 1];
}
public static long query(int jobl, int jobr, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
return sum[i];
}
int mid = l + ((r - l) >>
1);
down(i, mid - l + 1, r - mid);
long ans = 0;
if (jobl <= mid) {
ans = (ans + query(jobl, jobr, l, mid, i <<
1)) % m;
}
if (jobr > mid) {
ans = (ans + query(jobl, jobr, mid + 1, r, (i <<
1) | 1)) % m;
}
return (ans + m) % m;
}
public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {
if (jobl <= l && r <= jobr) {
lazyAdd(i, jobv, r - l + 1);
} else {
int mid = l + ((r - l) >>
1);
down(i, mid - l + 1, r - mid);
if (jobl <= mid) {
add(jobl, jobr, jobv, l, mid, i <<
1);
}
if (jobr > mid) {
add(jobl, jobr, jobv, mid + 1, r, (i <<
1) | 1);
}
buildSum(i);
}
}
private static void down(int i, int ln, int rn) {
if (mul[i] != 1) {
lazyMulti(i <<
1, mul[i]);
lazyMulti((i <<
1) | 1, mul[i]);
mul[i] = 1L;
}
if (add[i] != 0) {
lazyAdd(i <<
1, add[i], ln);
lazyAdd((i <<
1) | 1, add[i], rn);
add[i] = 0;
}
}
private static void lazyMulti(int i, long v) {
mul[i] = (mul[i] * v) % m;
add[i] = (add[i] * v) % m;
sum[i] = (sum[i] * v) % m;
}
private static void lazyAdd(int i, long v, int cnt) {
add[i] = (add[i] + v) % m;
sum[i] = (sum[i] + v * cnt) % m;
}
}

如有错误，欢迎指出！！！！

posted @ 2025-07-25 12:48 yfceshi 阅读(9) 评论(0) 收藏举报

刷新页面返回顶部