OO前三次求导作业总结

OO前三次作业，任务是表达式求导，其中包含简单幂函数和简单正余弦函数的导函数的求解。在三次难度递增的作业中，我对面向对象这一思想有了更为深入（然而还十分粗浅）的认识。

(1).程序结构分析

第一次作业，我使用了状态机的思想，将每个项分开，储存在一个ArrayList数组中，再提出求导。这时，我并没有任何面向对象的思想。没有分任何类，纯粹是面向过程的写法。

第二次作业，我开始使用面向对象的思想，构造了相应的类与方法。代码的可读性大大增加。但是，面对更复杂的组合，我为了省事，采用了大正则匹配的写法，为第三次作业埋下了隐患。

第三次作业难度陡增，因为出现了嵌套的表达式，不能再用大正则无脑匹配的方法，需要大幅度重构代码，我把自己的代码分为了expression（表达式），item（项），factor（因子）三个不同层次的类，其中包含了求导与匹配的方法。其中，exp与item结构相似，都包含一个ArrayList数组，以储存低一层的类；factor类中包含了幂函数，三角函数与表达式因子。

 

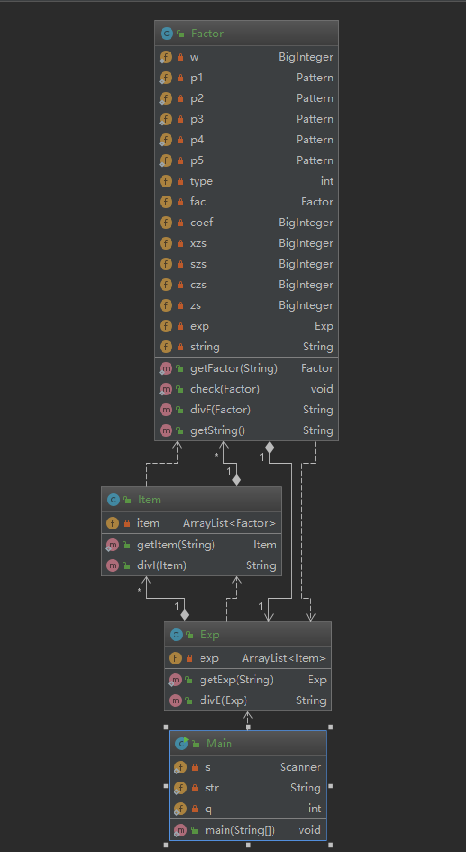
因为时间与能力所限，我的类构建得十分臃肿，命名和方法的使用都十分丑陋，在此就不详细地贴出来了。

匹配的方法是一个一个字符搜寻表达式（以+-号分割）和项（以*号分割），再使用小正则匹配每个因子。如果存在嵌套，则递归到下一层，再次搜寻表达式。

以下是对代码复杂度的分析：

 

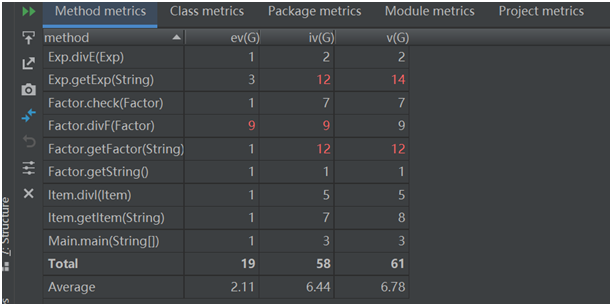
可以看到，ev(G),iv(G),v(G)都比较高，尤其是模块设计复杂度，圈复杂度非常高，说明程序的耦合度与结构的复杂程度仍处于一个比较高的水平，在之后的实验中，仍需要进一步改进。

(2).分析自己程序的bug

前三次作业中，我各出现了一个bug，但分析下来，都是过于简单的错误：

第一次作业，Bug出在没有熟读题目，没有判断‘ ’与‘\t’之外的空白字符。

第二次作业，Bug出在没有使用独占模式匹配，面对较长的表达式时，我的程序运行速度非常慢，导致虽然可以得到正确结果，却出现了超时错误。最终通过修改正则表达式为独占模式匹配，解决了问题。

第三次作业，Bug出在忘记输出表达式因子的系数（即正负号），和手滑打少了几个字母，导致无法识别^号与*号后的符号。

程序设计问题

在结构上，因为代码体量最大，我主要把分析重点放在第三次作业中。

首先，我的factor类中包括了幂函数，三角函数与表达式，因为没有使用接口和继承，结构比较冗余；另外，我的方法没有完全遵循“高内聚，低耦合”的原则，把多个不同的功能，如判断因子类型，提取系数、指数等功能，集合在一个方法里，导致方法体量过于庞大，无法控制在60行内。

因为时间问题，类中的许多元素都并非必须，例如在factor类中，我设置了四个BigInteger类储存不同函数的指数……导致修改代码变得极为麻烦。

三次作业，我总共改了6行代码，第二三次作业合计甚至只改了5个字符。可是，在第三次互测中，我被hack了18次（仅修改了两行代码就完全通过），由此引入下一个话题：如何发现bug，尤其是，发现不同质的bug。

(3).一些发现bug的策略

发现bug不难，但发现大量的不同质bug是一件难事。诸如对拍器等黑科技已经有不少大佬分享过了。在此，我抛砖引玉，分享自己纯手工找bug的一些心得：

1.新功能容易出bug，但更容易出bug的是新旧功能混杂的情况，可能新功能没问题，但在一些特殊情况下，会与旧体系冲突。例如判断sin（-7）与sin（- 7），我所见的不少代码都出现过二者均判断为正确或均判断为错误的问题；

2.针对讨巧的做法，它们经常通过特判甚至打表等不规范的做法回避一些问题，这时，通过将陷阱重复或移动陷阱位置的方法有时有奇效，例如加空白字符时敲两个以上，将数字因子放在x后。

3.当然，最有效的方法莫过于精读他人的代码。随着难度的增加，格式判断错误将不再是主流，与效率，数据结构有关的TLE 和 RTE会越来越多地出现在我们面前，只有增强自己的编程能力，才能有更强的debug能力。

(4).Applying Creational Pattern 

在三次作业中，我都出现了一个问题：方法耦合过于严重。许多核心方法，如求导，匹配因子的方法，我都没有将其中的功能细分，就比如如下代码：

 public static Factor getFactor(String str) {
        Factor factor = new Factor();
        factor.coef = BigInteger.valueOf(1);
        String strs = str;
        Matcher m1 = p1.matcher(strs);
        if (m1.matches()) {
            factor.type = 0;
            factor.string = "(" + str + ")";
            factor.coef = factor.coef.multiply(new BigInteger(m1.group()));
        } else {
            if (strs.charAt(0) == '+' || strs.charAt(0) == '-') {
                factor.coef = new BigInteger(str.charAt(0) + "1");
                strs = str.substring(1);
            }
            Matcher m2 = p2.matcher(strs);
            Matcher m3 = p3.matcher(strs);
            Matcher m4 = p4.matcher(strs);
            Matcher m5 = p5.matcher(strs);
            if (m2.matches()) {
                factor.string = "(" + str + ")";
                factor.type = 1;
                strs = strs.replaceAll("x\\^?", "");
                if (strs.length() != 0) {
                    factor.xzs = (new BigInteger(strs));
                } else {
                    factor.xzs = (BigInteger.valueOf(1));
                }
            } else if (m3.matches()) {
                factor.string = "(" + str + ")";
                factor.type = 2;
                factor.fac = getFactor(m3.group(1));
                strs = strs.replaceAll("sin\\(.*\\)(\\^)?", "");
                if (strs.length() != 0) {
                    factor.szs = (new BigInteger(strs));
                } else {
                    factor.szs = (BigInteger.valueOf(1));
                }
            } else if (m4.matches()) {
                factor.string = "(" + str + ")";
                factor.type = 3;
                factor.fac = getFactor(m4.group(1));
                strs = strs.replaceAll("cos\\(.*\\)(\\^)?", "");
                if (strs.length() != 0) {
                    factor.czs = (new BigInteger(strs));
                } else {
                    factor.czs = (BigInteger.valueOf(1));
                }
            } else if (m5.matches()) {
                factor.string = "(" + str + ")";
                factor.type = 4;
                strs = strs.replaceAll("\\(.*\\)(\\^)?", "");
                if (strs.length() != 0) {
                    factor.zs = (new BigInteger(strs));
                } else {
                    factor.zs = (BigInteger.valueOf(1));
                }
                factor.exp = Exp.getExp(m5.group(1));
            } else {
                System.out.println("WRONG FORMAT!");
                System.exit(0);
            }
            check(factor);
        }
        return factor;
    }

这是一个输入一个表示因子的字符串，返回一个因子类的方法。其中包括了判断因子类型和储存系数指数的功能，因为不同的因子储存的方法略有不同，我一直没有把它们分开，然而，我们完全可以将其分为一个judgeType方法与5个store方法，大大提升代码的可读性，复用性与可维护性。

认识与感想

目前最难的第三次作业，因为出现了嵌套的表达式，不能再用大正则无脑匹配的方法，导致我在匹配过程中被卡了近两天，最后还码出了一份错误的匹配代码。

后来，我重新理顺自己的思路，重写代码，将表达式分为expression（表达式），item（项），factor（因子）三大层次，通过层层递归地匹配方法，成功地匹配成功。建立了一个成功的数据结构后，求导也变得十分简单了。我从推倒重来到最终完成作业，仅用了12个小时（虽然为赶上ddl放弃了优化与部分风格分）。相比于一股脑的瞎码代码，在动手前建立一个完善的数据结构，更助于项目的完成。

在肝代码的过程中，我发现，面向对象的思想在代码构建的过程中可以使我们代码的结构变得规整，优美，也便于维护与功能扩展。面对越来越复杂的作业与项目，面向对象的思想将成为我们致胜的法宝。