GAMES101 | 作业2：Triangles and Z-buffering

1.作业内容

在屏幕上画出一个实心三角形，换言之，栅格化一个三角形。

2.任务分析

rasterize_triangle()中分为以下几步操作：

2.1创建三角形的2维bounding box

这一步就是计算出三角形平行于坐标轴的外接矩形，减少计算量。

    int xmin = floor(std::min(v[0][0],std::min(v[1][0],v[2][0])));
    int xmax = ceil(std::max(v[0][0],std::max(v[1][0],v[2][0])));
    int ymin = floor(std::min(v[0][1],std::min(v[1][1],v[2][1])));
    int ymax = ceil(std::max(v[0][1],std::max(v[1][1],v[2][1])));

2.2遍历像素

遍历上一步的bounding box内的所有像素（使用其整数索引）。然后，使用像素中心(x+0.5,y+0.5)的屏幕空间坐标来检查中心点是否在三角形内。

这里涉及到insideTriangle()函数，判断点P是否在给定三角形ABC内，应用了向量叉积的性质，分别计算\(PA×AB\)，\(PB×BC\)，\(PC×CA\)，若结果指向同一方向即可判定点P在三角形内。

由于本任务在投影变换之后，三角形顶点坐标在这一步可以看作在同一z平面上，简化判定。

static bool insideTriangle(int x, int y, const Vector3f* _v){  
    float fx=(float)x;
    float fy=(float)y;
    Vector3f p(fx,fy,1.0f); 
    Vector3f px[3],xy[3],vt[3],cr[3];
    for(int i=0;i<3;i++)vt[i]<<_v[i].x(),_v[i].y(),1.0f;
    for(int i=0;i<3;i++){
        px[i]=p-vt[i];
        xy[i]=vt[(i+1)%3]-vt[i];
        cr[i]=px[i].cross(xy[i]);
    }
    if((cr[0][2]>0&&cr[1][2]>0&&cr[2][2]>0)||(cr[0][2]<0&&cr[1][2]<0&&cr[2][2]<0)){
        return true;
    }
    else{
        return false;
    }
}

2.3插值计算内部点的深度

这一步应用了框架中的代码。

2.4更新depth_buf

将该点插值出的z坐标z_interpolated与depth_buf中对应记录比较，如果当前点更靠近相机，设置像素颜色并更新深度缓冲区depth_buf。

  float x=i+0.5;
  float y=j+0.5;
  if(insideTriangle(x,y,t.v)){
      //插值
      auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
      float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
      float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
      z_interpolated *= w_reciprocal;

      if(z_interpolated < depth_buf[get_index(i,j)]){
          depth_buf[get_index(i,j)]=z_interpolated;
          Eigen::Vector3f cur(i,j,z_interpolated);
          set_pixel(cur,t.getColor());//着色
      }
  }

2.5输出

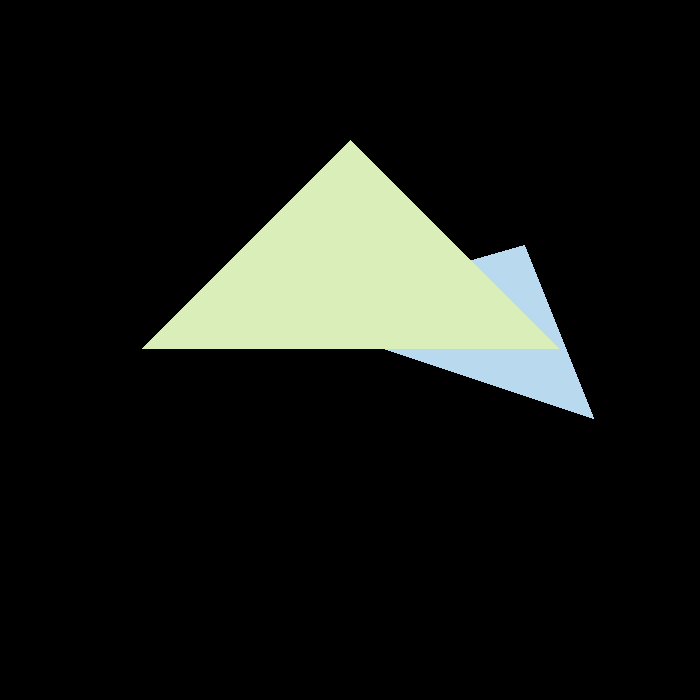
3.提高部分

3.1多重采样抗锯齿MultiSampling Anti-Aliasing(MASS)原理

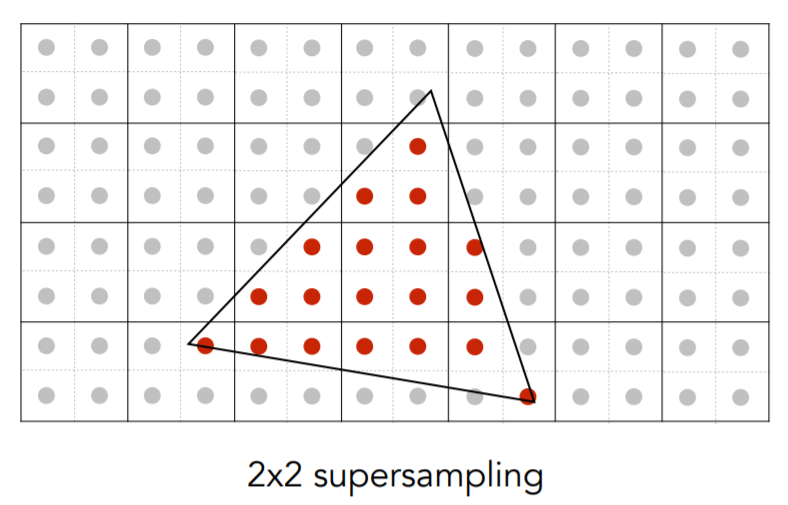
将原本的每个像素\(N×N\)划分，得到\(N^2\)个采样点，对这些点分别着色，最终原像素的值取这些点的平均值，与三角形重合较多的像素颜色更接近该三角形本身。

3.2代码实现

这里我们对每个像素进行2*2采样，实现上，定义四倍大的ss_depth_buf和ss_frame_buf用于子像素的采样。
需要注意的是，由于一单位坐标被分成了4块，insideTriangle()的参数不再是整数，需要修改原框架上的定义。

新二维向量的定义及初始化：

//定义
std::vector< std::vector<Eigen::Vector3f> > ss_frame_buf;
std::vector< std::vector<float> > ss_depth_buf;

//初始化
void rst::rasterizer::clear(rst::Buffers buff)
{
    if ((buff & rst::Buffers::Color) == rst::Buffers::Color)
    {
        std::fill(frame_buf.begin(), frame_buf.end(), Eigen::Vector3f{0, 0, 0});
        for (int i = 0; i < ss_frame_buf.size(); i++) {
            ss_frame_buf[i].resize(4);
            std::fill(ss_frame_buf[i].begin(), ss_frame_buf[i].end(), Eigen::Vector3f{ 0, 0, 0 });
        }
    }
    if ((buff & rst::Buffers::Depth) == rst::Buffers::Depth)
    {
        std::fill(depth_buf.begin(), depth_buf.end(), std::numeric_limits<float>::infinity());
        for (int i = 0; i < ss_depth_buf.size(); i++) {
            ss_depth_buf[i].resize(4);
            std::fill(ss_depth_buf[i].begin(), ss_depth_buf[i].end(), std::numeric_limits<float>::infinity());
        }
    }
}
rst::rasterizer::rasterizer(int w, int h) : width(w), height(h)
{
    frame_buf.resize(w * h);
    depth_buf.resize(w * h);
    ss_frame_buf.resize(w * h);
    ss_depth_buf.resize(w * h);
}

实现：

for(int i=xmin;i<=xmax;i++){
    for(int j=ymin;j<=ymax;j++){
        std::vector<Eigen::Vector2f> pos{
            {0.25,0.25},{0.75,0.25},
            {0.25,0.75},{0.75,0.75},
        };
        for(int k=0;k<4;k++){
            float x=i+pos[k][0];
            float y=j+pos[k][1];
            if(insideTriangle(x,y,t.v)){
                auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
                float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
                if(z_interpolated < ss_depth_buf[get_index(i,j)][k]){
                    ss_depth_buf[get_index(i,j)][k]=z_interpolated;
                    Eigen::Vector3f cur(i,j,z_interpolated);
                    ss_set_pixel(cur,t.getColor(),k);
                }
            }
        }
    }
}

3.3输出

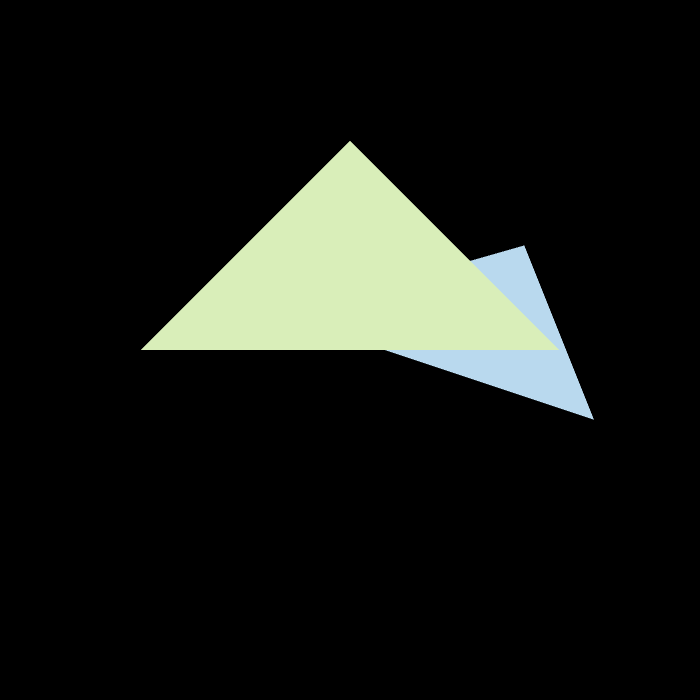
3.4结果对比

左图为原始方法，右图为MASS优化后的结果，可以清晰对比看出优化后显著减少了锯齿。