数据结构与算法（12）——动态规划案例

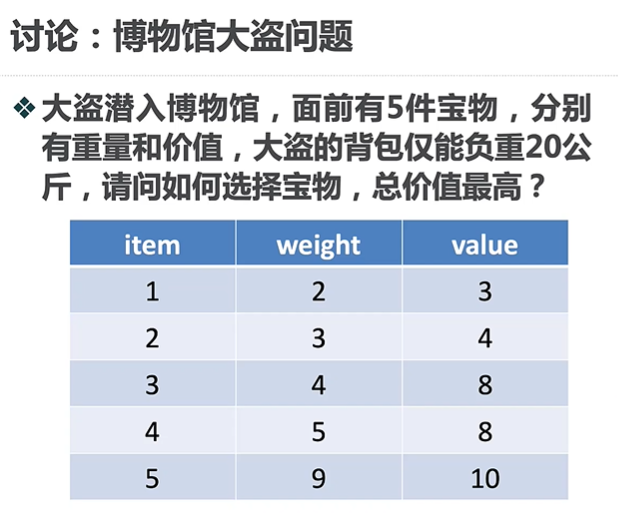
• 博物馆大盗问题

问题描述如下：

 

 

•  动态规划解决问题的分析

前i（1<=i<=5）个宝物中，组合不超过w(1<=w<=20)重量，得到的最大价值函数：

 

 其中，当i=0，w=0时，表示取不到，第三种情况表示第i件的重量超过了w的重量，则选第i-1件宝物，第4种选择表示从选第i件和第i-1件宝物的最优选择。

但其实选择的过程中，是遍历这样一个表的过程：

 

 其实就是一个不断递推回去的过程。

这里m(5,5) = m(4,5)= max(m(3,5),m(3,0) + 8)

• 代码

 

tr = [None, {'w':2,'v':3}, #重量和价值
      {'w':3,'v':4},
      {'w':4,'v':8},
      {'w':5,'v':8},
      {'w':9,'v':10}]
max_w = 20
#初始化二维表格m[i,w]
m = {(i, w):0 for i in range(len(tr))
     for w in range(max_w+1)}

#逐个填写表格
for i in range(1,len(tr)):
    for w in range(1, max_w + 1):
        if tr[i]['w'] > w: #装不下第i个宝物
            m[(i, w)] = m[(i-1, w)] #不装第i个宝物
        else:
            #不装第i个，装第i-1个和装第i个宝物的最大价值
            m[(i, w)] = max(m[(i-1, w)], m[(i-1, w-tr[i]['w'])] + tr[i]['v'])
print(m[(len(tr) -1), max_w])