寒假集训专题七:图论入门
ESAY1:Stockbroker Grapevine

解题思路:
这道题我们先分析它的数据大小和数据间关系,我们可以得知这道题是小规模的寻找单一源头的最短路径问题,我们要使最长的一条路径长度最小。我们可以选择两种方法:遍历每一个源点运用Dijkstra算法(实现比较麻烦);floyd算法。通过图论学习,对于这种小规模的边数较多的图,求多源最短路径问题,我们一般选用floyd算法。
我们通过floyd更新距离矩阵然后遍历所有结点,将其作为原点,更新最远距离,再更新最终答案。最终将答案与我们一开始预设的无穷大作比较,如果相等说明所有点之间是不连通的,输出disjoint,否则输出结果。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 110;
const int INF = 0x3f;
int dist[maxn][maxn];
int n;
void init()
{
memset( dist, INF, sizeof( dist ) );
for( int i = 1; i <= n; i++ )
{
dist[i][i] = 0;
}
return;
}
void floyd()
{
for( int k = 1; k <= n; k++ )
{
for( int i = 1; i <= n; i++ )
{
for( int j = 1; j <= n; j++ )
{
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
int pos = 0;
int ans = INF;
for( int i = 1; i <= n; i++ )
{
int temp = 0;
for( int j = 1; j <= n; j++ )
{
if( i != j )
{
temp = max( temp, dist[i][j] );
}
}
if( temp < ans )
{
pos = i;
ans = temp;
}
}
if( ans == INF )
{
printf( "disjoint\n" );
}
else
{
printf( "%d %d\n", pos, ans );
}
}
int main()
{
while( ~scanf( "%d", &n ) && ( n != 0 ) )
{
init();
for( int i = 1; i <= n; i++ )
{
int x;
scanf( "%d", &x );
for( int j = 1; j <= x; j++ )
{
int no, dis;
scanf( "%d %d", &no, &dis );
dist[i][no] = dis;
}
}
floyd();
}
}
ESAY2:树的直径
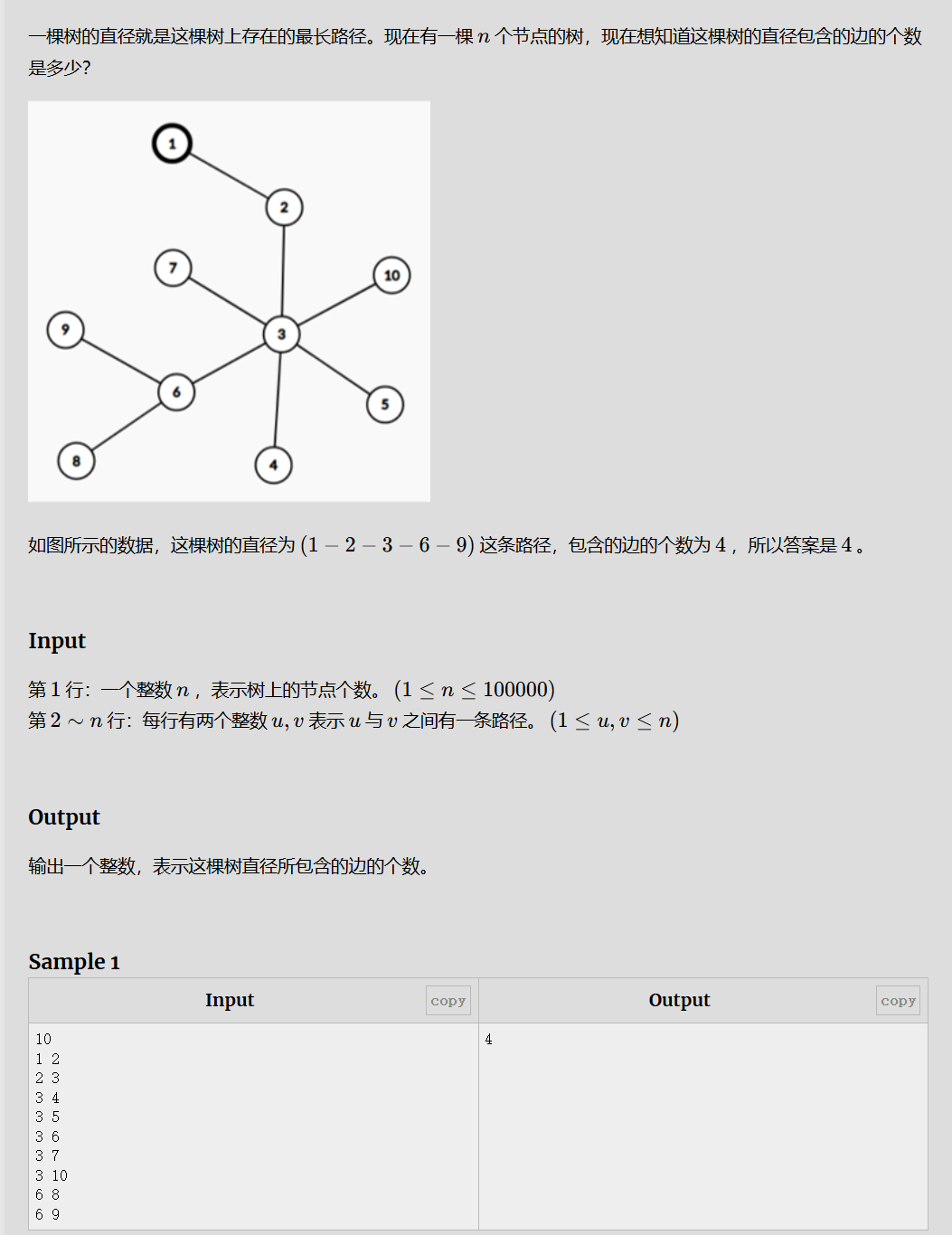
解题思路:
这道题使用树形dp是较好的解决方法,对于添加边,我们把图绘制下来,然后选取一个点,遍历它的子节点,只要它不是父节点,就递归更新子节点的状态,在更新节点状态之前,先更新答案,dp[u]为当前节点为根子树最大的直径,同理,答案可以更新为原答案和两子树最大直径和加一。最后更新该点最大直径状态为dp[v]+1。最后结果就是最开始选取点dp[u]。
也可以用dfs()找到一个点,然后再从这个点dfs()求出最远点,得到最大距离。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
vector<int> g[maxn];
int dis[maxn];
int ans = 0;
void dp( int u, int fa )
{
for( auto& v : g[u] )
{
if( v == fa ) continue;
dp( v, u );
ans = max( ans, dis[u] + dis[v] + 1 );
dis[u] = max( dis[u], dis[v] + 1 );
}
}
int main()
{
int n;
cin >> n;
memset( dis, 0, sizeof(int) * ( n + 1 ) );
for( int i = 1; i < n; i++ )
{
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dp( 1, 0 );
cout << ans << endl;
return 0;
}
//#include<bits/stdc++.h>
//using namespace std;
//
//const int maxn = 1e5+6;
//int n;
//int ans = 0, farNode = 0;
//vector<int> graph[maxn];
//
//void dfs( int cur_node, int fathernode, int d )
//{
// if( d > ans )
// {
// ans = d;
// farNode = cur_node;
// }
// for( int v : graph[cur_node] )
// {
// if( v != fathernode )
// {
// dfs( v, cur_node, d + 1 );
// }
// }
//}
//
//
//int main()
//{
// cin >> n;
//
// for( int i = 1; i < n; i++ )
// {
// int x, y;
// cin >> x >> y;
// graph[x].push_back(y);
// graph[y].push_back(x);
// }
//
// dfs( 1, -1, 0 );
//
// ans = 0;
//
// dfs( farNode, -1, 0 );
//
// cout << ans << "\n";
//
// return 0;
//
//}
MEDIUM1: Invitation Cards

解题思路:
这道题数据范围很大,且是单源问题,所以我们选择用Dijkstra算法,这道题主要的核心在于如何反向建图,我们先用dijkstra算法进行正向建图,之后我们要得到每个点到源点的花费的总和最小值,我们可以想一下,在一个有向图里面,我们把边反向之后,从一个源点发出的图是不是就变成会聚在源点的图,出于这个考虑,我们在初始化图的时候选择用mp来存储正向的初始边,同时用remp存储反向的初始边,然后在对于mp的dijkstra函数中用dist来存储正向结果,同理remp也要存储。
dijkstra函数中利用优先队列维护能到达的最短距离,将当前起始点推入队列,然后对于邻接边中能更新最短距离的点推入队列,如果当前距离已更新过,跳过。
最后只要从2号点开始遍历,将其在正反两图的和加入到答案中,就是最终答案了。
#include <iostream>
#include <cstring>
#include <vector>
#include <climits>
#include <queue>
#include <algorithm>
#include <functional>
#define ll long long
using namespace std;
const int maxn = 1e6+7;
const ll INF = 0x3f3f3f3f3f3f3f3f;
vector<pair<int,int>> mp[maxn];
vector<pair<int,int>> remp[maxn];
ll dist_first[maxn], dist_second[maxn];
int P,Q,T;
ll ans;
void dijkstra( int start, int n, long long dist[], vector<pair<int,int>> mp[] )
{
priority_queue< pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>> > pq;
memset( dist, INF, sizeof( ll ) * ( P + 1 ) ) ;
dist[start] = 0;
pq.push( { start, 0 } );
while( !pq.empty() )
{
int cur = pq.top().first;
long long cur_dist = pq.top().second;
pq.pop();
if( cur_dist > dist[cur] ) continue;
for( auto& edge : mp[cur] )
{
int to = edge.first;
ll weight = edge.second;
if( dist[cur] + weight < dist[to] )
{
dist[to] = dist[cur] + weight;
pq.push( { to, dist[to] } );
}
}
}
}
int main()
{
ios::sync_with_stdio(false); // 加速输入输出
cin.tie(nullptr);
cin >> T;
while( T-- )
{
cin >> P >> Q;
for( int i = 1; i <= P; i++ )
{
mp[i].clear();
remp[i].clear();
}
while( Q-- )
{
int u, v;
ll w;
cin >> u >> v >> w;
mp[u].push_back( { v, w } );
remp[v].push_back( { u, w } );
}
dijkstra( 1, P, dist_first, mp );
dijkstra( 1, P, dist_second, remp );
ll total_cost = 0;
for( int i = 2; i <= P; i++ )
{
total_cost += dist_first[i] + dist_second[i];
}
cout << total_cost << "\n";
}
return 0;
}
MEDIUM2:战略游戏
P2016 战略游戏
题目背景
Bob 喜欢玩电脑游戏,特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。
题目描述
他要建立一个古城堡,城堡中的路形成一棵无根树。他要在这棵树的结点上放置最少数目的士兵,使得这些士兵能瞭望到所有的路。
注意,某个士兵在一个结点上时,与该结点相连的所有边将都可以被瞭望到。
请你编一程序,给定一树,帮 Bob 计算出他需要放置最少的士兵。
输入格式
第一行一个整数 \(n\),表示树中结点的数目。
第二行至第 \(n+1\) 行,每行描述每个结点信息,依次为:一个整数 \(i\),代表该结点标号,一个自然数 \(k\),代表后面有 \(k\) 条无向边与结点 \(i\) 相连。接下来 \(k\) 个整数,分别是每条边的另一个结点标号 \(r_1,r_2,\cdots,r_k\),表示 \(i\) 与这些点间各有一条无向边相连。
对于一个 \(n\) 个结点的树,结点标号在 \(0\) 到 \(n-1\) 之间,在输入数据中每条边只出现一次。保证输入是一棵树。
输出格式
输出文件仅包含一个整数,为所求的最少的士兵数目。
输入输出样例 #1
输入 #1
4
0 1 1
1 2 2 3
2 0
3 0
输出 #1
1
说明/提示
数据规模与约定
对于全部的测试点,保证 \(1 \leq n \leq 1500\)。
解题思路:
树形dp的常用场景求树的最小点覆盖,我们先用邻接表将树存储下来,然后来定义一下树的状态dp[x][0]为不选中该点,dp[x][1]为选中该点。
从0号点开始遍历0点的每一个邻接点,如果邻接点与父节点相同,跳过。如果是在选用该点情况下无论是否选用邻接点都是可以的,加上最小值便是,如果不选用该点,那子节点应该都选择,所以求其和。
最后返回答案dp[0][0]和dp[0][1]的最小值就是最终答案。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1510;
vector<int> g[maxn];
int ans[maxn][2];
void dp( int x, int fa )
{
ans[x][1] = 1,//放士兵
ans[x][0] = 0;//不放士兵
for( auto& y : g[x] )
{
if( y == fa ) continue;
dp( y, x );
ans[x][1] += min( ans[y][0], ans[y][1] );
ans[x][0] += ans[y][1];
}
}
int main()
{
int n;
cin >> n;
for( int i = 0; i < n; i++ )
{
int u, v, t;
cin >> u >> t;
while( t-- )
{
cin >> v;
g[u].push_back( v );
g[v].push_back( u );
}
}
dp( 0, -1 );
cout << min( ans[0][1], ans[0][0] ) << endl;
return 0;
}
学习总结:
一共三种最短路问题的算法:
floyd算法适用于多源最短路径问题,时空复杂度都高,所以比较适合小规模图问题。
dijkstra算法适合正权图的单元最短路径问题,用了优先队列来优化时间复杂度,对于稀疏图,效率较高。
spfa算法用来解决dijkstra算法解决不了的负权边问题。
//floyd算法
for( int k = 1; k <= n; k++ )
{
for( int i = 1; i <= n; i++ )
{
for( int j = 1; j <= n; j++ )
{
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
//拓展一下floyd算法的最小环问题
for( int k = 1; k <= N; k++ )
{
//更新答案
for( int i = 1; i < k; i++ )
{
for( int j = i + 1; j < k; j++ )
{
ans = min( ans, cost[i][j] + w[i][k] + w[k][j] );
}
}
//更新最短距离矩阵
for( int i = 1; i <= N; i++ )
{
for( int j = 1; j <= N; j++ )
{
cost[i][j] = min( cost[i][j], cost[i][k] + cost[k][j] );
}
}
}
//dijkstra算法 有点类似dfs
void dijkstra( int start, int n, long long dist[], vector<pair<int,int>> mp[] )
{
priority_queue< pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>> > pq;
memset( dist, INF, sizeof( ll ) * ( P + 1 ) ) ;
dist[start] = 0;
pq.push( { start, 0 } );
while( !pq.empty() )
{
int cur = pq.top().first;
long long cur_dist = pq.top().second;
pq.pop();
if( cur_dist > dist[cur] ) continue;
for( auto& edge : mp[cur] )
{
int to = edge.first;
ll weight = edge.second;
if( dist[cur] + weight < dist[to] )
{
dist[to] = dist[cur] + weight;
pq.push( { to, dist[to] } );
}
}
}
}
//spfa没咋用过
......
//树形dp
void dp( int u, int fa )
{
for( auto& v : g[u] )
{
if( v == fa ) continue;
dp( v, u );
ans = max( ans, dis[u] + dis[v] + 1 );
dis[u] = max( dis[u], dis[v] + 1 );
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号