寒假集训专题五:搜索
ESAY1:自然数的拆分
P2404 自然数的拆分问题
题目描述
任何一个大于 \(1\) 的自然数 \(n\),总可以拆分成若干个小于 \(n\) 的自然数之和。现在给你一个自然数 \(n\),要求你求出 \(n\) 的拆分成一些数字的和。每个拆分后的序列中的数字从小到大排序。然后你需要输出这些序列,其中字典序小的序列需要优先输出。
输入格式
输入:待拆分的自然数 \(n\)。
输出格式
输出:若干数的加法式子。
输入输出样例 #1
输入 #1
7
输出 #1
1+1+1+1+1+1+1
1+1+1+1+1+2
1+1+1+1+3
1+1+1+2+2
1+1+1+4
1+1+2+3
1+1+5
1+2+2+2
1+2+4
1+3+3
1+6
2+2+3
2+5
3+4
说明/提示
数据保证,\(2\leq n\le 8\)。
解题思路:
这种有点类似于全排列这种类型,需要枚举每一种有可能的组合,我们就会使用dfs来进行每一种组合的筛选。
首先我们需要一个数组来存储当前已选择的数字,以及记录当前选择的数字和所剩的余额。
我们观察样例输出的形式,所以我们从1开始进行搜索,搜索一直进行到全选1输出完,然后往回退一步,回到选出倒二个1的时候选用2.
以此类推,我们再dfs中需要遍历当前选用数字到剩余数字全部的结果。
终止条件的判断,因为我们在遍历中将选择数字大小约束在<=rest的范围内,所以再次调用时rest一定不会出现负数情况,当rest不等于0时只能说明当前数字选择不能够分解给定有理数,我们直接判断rest是否等于0就行。
最后是考虑特殊状况,我们注意到样例输出时,没有出现要被拆分的有理数本身,所以我们将满足rest==0但是数组大小仅有1的情况排除。
#include<bits/stdc++.h>
using namespace std;
void dfs(vector<int>& prim, int rest, int cur_num) {
if (rest == 0) {
if( prim.size() == 1 )
{
return;
}
else
{
// 输出当前分解式
for( int i = 0; i < prim.size(); i++ )
{
cout << prim[i] << ( i == prim.size()-1 ? "\n" : "+" );
}
return;
}
}
// 尝试所有可能的数字
for (int i = cur_num; i <= rest; i++) {
prim.push_back(i);
dfs(prim, rest - i, i); // 递归调用
prim.pop_back(); // 回溯
}
}
int main() {
vector<int> prim;
int n;
cin >> n;
dfs(prim, n, 1);
return 0;
}
ESAY2:填涂颜色
P1162 填涂颜色
题目描述
由数字 \(0\) 组成的方阵中,有一任意形状的由数字 \(1\) 构成的闭合圈。现要求把闭合圈内的所有空间都填写成 \(2\)。例如:\(6\times 6\) 的方阵(\(n=6\)),涂色前和涂色后的方阵如下:
如果从某个 \(0\) 出发,只向上下左右 \(4\) 个方向移动且仅经过其他 \(0\) 的情况下,无法到达方阵的边界,就认为这个 \(0\) 在闭合圈内。闭合圈不一定是环形的,可以是任意形状,但保证闭合圈内的 \(0\) 是连通的(两两之间可以相互到达)。
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 1 0 1
1 1 1 1 1 1
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 1 2 1
1 1 1 1 1 1
输入格式
每组测试数据第一行一个整数 \(n(1 \le n \le 30)\)。
接下来 \(n\) 行,由 \(0\) 和 \(1\) 组成的 \(n \times n\) 的方阵。
方阵内只有一个闭合圈,圈内至少有一个 \(0\)。
输出格式
已经填好数字 \(2\) 的完整方阵。
输入输出样例 #1
输入 #1
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
输出 #1
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
说明/提示
对于 \(100\%\) 的数据,\(1 \le n \le 30\)。
解题思路:
这种连通块的问题就像课件里给出那道水坑问题一样,如果一块一块地调用dfs()效率低下,所以我们采用了bfs()。
这道题其实需要采用一种比较巧妙的做法,因为直接去找闭合圈中的0并不是简单的事,如果一个一个判断条件(触壁是1还是边界)真的很麻烦。我们就考虑是不是可以找闭合圈外的0呢。
但是,这时候就出现一个问题,就是bfs()在水坑问题里判断水坑数量是从连通性上来判断的,我们在闭合圈外的0区域可能不具有连通性,这样问题怎么解决?
我们可以想一下,正方形的矩阵,将外围区域扩大一整圈,然后填上0,是不是闭合圈外所有的0都联通上了,这时候我们可以从mp数组的[0][0]位置开始进行bfs()搜索,将所有在闭合圈外的0连通起来,并且在访问数组中将这些0赋值为已被访问。(记得把1也赋值成已被访问,当作墙壁避免回头)
这样就能在输出时进行判断,如果mp中是1就正常输出,如果是0就再次进行判断,如果已被访问,那就输出0,没被访问就输出2.
(也可以用dfs(),因为目的是标记不在闭合圈内的0,只要搜索之后记录就行了,就是还要把边界搜索一下,以防标记到闭合圈内的0)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 32;
int n;
vector<vector<int>> mp( maxn, vector<int>( maxn, 0 ) );
vector<vector<bool>> vis( maxn, vector<bool>( maxn, false ) );
void bfs( int i, int j )
{
if( i < 0 || i > n+1 || j < 0 || j > n+1 || vis[i][j] )
{
return;
}
vis[i][j] = true;
vector<vector<int>> directions =
{ { -1, 0 }, { 0, -1 }, { 0, 1 }, { 1, 0 } };
for( auto dir : directions )
{
bfs( i + dir[0], j + dir[1] );
}
}
int main()
{
cin >> n;
for( int i = 1 ; i <= n; i++ )
{
for( int j = 1; j <= n; j++ )
{
cin >> mp[i][j];
if( mp[i][j] == 1 )
{
vis[i][j] = true;
}
}
}
bfs(0, 0);
for( int i = 1 ; i <= n; i++ )
{
for( int j = 1; j <= n; j++ )
{
if( mp[i][j] == 1 )
{
cout << mp[i][j] << ( j == n ? "\n" : " " );
}
else
{
if( vis[i][j] )
{
cout << 0 << ( j == n ? "\n" : " " );
}
else
{
cout << 2 << ( j == n ? "\n" : " " );
}
}
}
}
return 0;
}
MEDIUM1:显示图像
P1256 显示图像
题目描述
古老的显示屏是由 \(N \times M\) 个像素(Pixel)点组成的。一个像素点的位置是根据所在行数和列数决定的。例如 \(P(2,1)\) 表示第 \(2\) 行第 \(1\) 列的像素点。那时候,屏幕只能显示黑与白两种颜色,人们用二进制 \(0\) 和 \(1\) 来表示。\(0\) 表示黑色,\(1\) 表示白色。当计算机发出一个指令:\(P(x,y)=1\),则屏幕上的第 \(x\) 行第 \(y\) 列的阴极射线管就开始工作,使该像素点显示白色,若 \(P(x,y)=0\),则对应位置的阴极射线管不工作,像素点保持黑色。在某一单位时刻,计算机以 \(N \times M\) 二维 \(01\) 矩阵的方式发出显示整个屏幕图像的命令。
例如,屏幕是由 \(3 \times 4\) 的像素点组成,在某单位时刻,计算机发出如下命令:
对应屏幕显示应为:
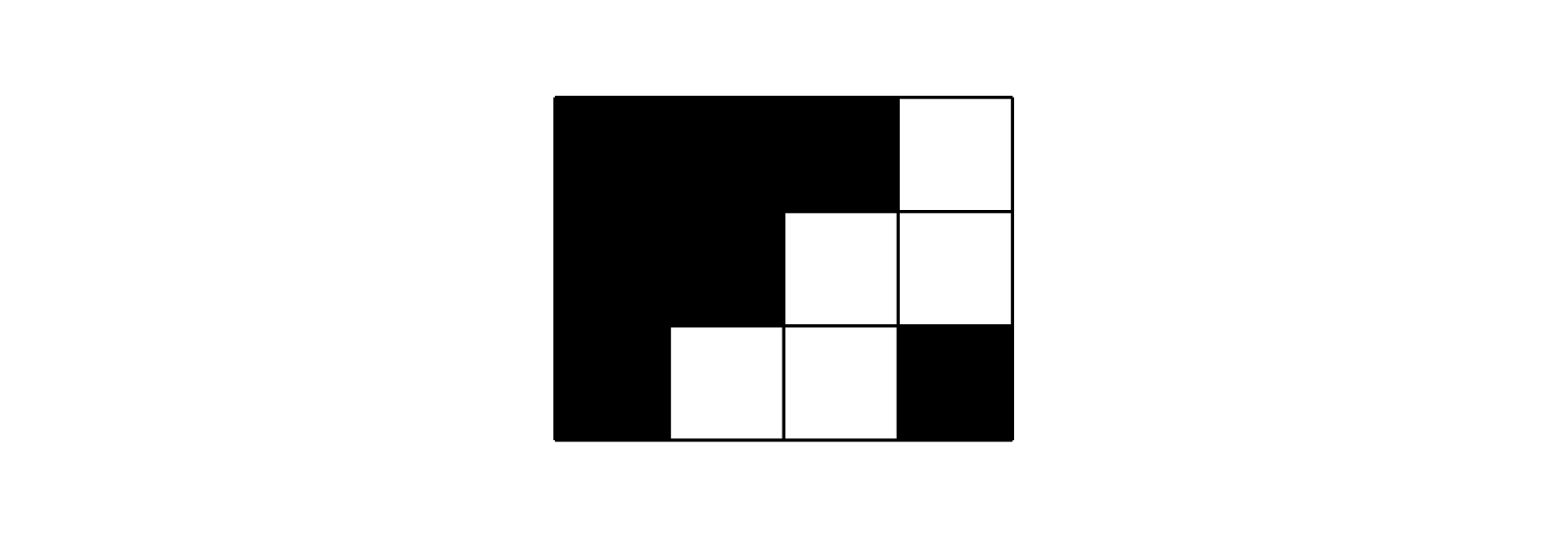
假设放大后,一个格子表示一个像素点。
由于未知的原因,显示黑色的像素点总是受显示白色的像素点的影响——可能是阴极射线管工作的作用。并且,距离越近,影响越大。这里的距离定义如下:
设有像素点 \(P_1(x_1,y_1)\) 和像素点 \(P_2(x_2,y_2)\),则它们之间的距离 \(D(P_1,P_2)=|x_1-x_2|+|y_1-y_2|\)。
在某一时刻,计算机发出显示命令后,科学家们期望知道,每个像素点和其最近的显示白色的像素点之间的最短距离是多少——科学家们保证屏幕上至少有一个显示白色的像素点。
上面的例子中,像素 \(P(1,1)\) 与最近的白色像素点之间的距离为 \(3\),而像素 \(P(3,2)\) 本身显示白色,所以最短距离为 \(0\)。
输入格式
第一行有两个数字,\(N\) 和 \(M\ (1 \le N,M \le 182)\),表示屏幕的规格。
以下 \(N\) 行,每行 \(M\) 个数字,\(0\) 或 \(1\)。为计算机发出的显示命令。
输出格式
输出文件有 \(N\) 行,每行 \(M\) 个数字,中间用 \(1\) 个空格分开。第 \(i\) 行第 \(j\) 列的数字表示距像素点 \(P(i,j)\) 最近的白色像素点的最短距离。
输入输出样例 #1
输入 #1
3 4
0001
0011
0110
输出 #1
3 2 1 0
2 1 0 0
1 0 0 1
说明/提示
- 对于 \(30\%\) 的数据:\(N\times M \le 10000\);
- 对于 \(100\%\) 的数据:\(N\times M \le 182^2\)。
解题思路:
这道题有这类最短路径的要求,我们就可以考虑运用bfs()函数进行搜索。
但是这道题从黑色块开始搜索,我们可能要调用多次函数,所以我们换个思路,我们可以从白色显示块开始,对黑色块进行搜索。
在搜索途中对搜索过的黑色块进行标记,记录下当前是搜索的第几步,记录下当作白色快到该色块的距离。
本质上是把搜索过的黑色块记录距离后当成白色块遍历搜索。
要注意输入时01是连起来的,我选用的是按字符串处理,也可以按字符单个输入。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 182;
vector<vector<int>> mp;
vector<vector<bool>> vis( maxn, vector<bool>( maxn, false ) );
vector<vector<int>> dis( maxn, vector<int>( maxn, -1 ) );
vector<vector<int>> directions = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };
int n, m;
void bfs()
{
queue<pair<int,int>> q;
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < m; j++ )
{
if( mp[i][j] == 1 )
{
dis[i][j] = 0;
vis[i][j] = true;
q.push( { i, j } );
}
}
}
while( !q.empty() )
{
auto node = q.front();
q.pop();
for( auto& dir : directions )
{
int ni = node.first + dir[0];
int nj = node.second + dir[1];
if( ni >= 0 && ni < n && nj >= 0 && nj < m && !vis[ni][nj] )
{
dis[ni][nj] = dis[node.first][node.second] + 1;
vis[ni][nj] = true;
q.push( { ni, nj } );
}
}
}
}
int main()
{
cin >> n >> m;
mp.resize( n, vector<int>( m ) );
queue<pair<int,int>> q;
for( int i = 0; i < n; i++ )
{
string s;
cin >> s;
for( int j = 0; j < m; j++ )
{
mp[i][j] = s[j] - '0';
}
}
bfs();
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < m; j++ )
{
cout << dis[i][j] << ( j == m - 1 ? "\n" : " " );
}
}
return 0;
}
MEDIUM2:健康的荷斯坦奶牛
P1460 [USACO2.1] 健康的荷斯坦奶牛 Healthy Holsteins
题目描述
农民 John 以拥有世界上最健康的奶牛为傲。他知道每种饲料中所包含的牛所需的最低的维他命量是多少。请你帮助农夫喂养他的牛,以保持它们的健康,使喂给牛的饲料的种数最少。
给出牛所需的最低的维他命量,输出喂给牛需要哪些种类的饲料,且所需的饲料剂量最少。
维他命量以整数表示,每种饲料最多只能对牛使用一次,数据保证存在解。
输入格式
第一行一个整数 \(v\),表示需要的维他命的种类数。
第二行 \(v\) 个整数,表示牛每天需要的每种维他命的最小量。
第三行一个整数 \(g\),表示可用来喂牛的饲料的种数。
下面 \(g\) 行,第 \(n\) 行表示编号为 \(n\) 饲料包含的各种维他命的量的多少。
输出格式
输出文件只有一行,包括牛必需的最小的饲料种数 \(p\);后面有 \(p\) 个数,表示所选择的饲料编号(按从小到大排列)。
如果有多个解,输出饲料序号最小的(即字典序最小)。
输入输出样例 #1
输入 #1
4
100 200 300 400
3
50 50 50 50
200 300 200 300
900 150 389 399
输出 #1
2 1 3
说明/提示
【数据范围】
对于 \(100\%\) 的数据,\(1\le v \le 25\),\(1\le g \le 15\)。
输入的所有整数在 \([1,1000]\) 范围内。
USACO 2.1
翻译来自NOCOW
解题思路:
是要求输出组合的题目,我们就会容易想到运用dfs()来解题。
首先分析一下我们需要存储奶牛的需求,还有饲料的信息,以及存储答案的临时数组和最终答案的数组,最后我都选用vector。
然后,考虑我们dfs()递归调用的终止条件,就是当我们选用的饲料,每一项都达到需求。除此之外,还要考虑是否是最小的饲料种类。
做一个大小判断,如果更小就直接替换掉答案,这里可能会考虑很多什么后面提到的字典序的大小问题,c++里面可以直接比较大小,不过这里因为递归调用后出现的最早答案一定是最小字典序的,所以这里不判断也是可以的。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1001;
vector<int> ans(maxn);
vector<int> temp(maxn);
vector<int> need(maxn);
vector<vector<int>> im( maxn, vector<int>( maxn, 0 ) );
int v, g;
int minn = INT_MAX;
bool check( int s )
{
for( int i = 1; i <= v; i++ )
{
int sum = 0;
for( int j = 1; j <= s; j++ )
{
sum += im[temp[j]][i];
}
if( sum < need[i] )
{
return false;
}
}
return true;
}
void dfs( int t, int s )
{
if( t > g )
{
if( check(s) )
{
if( s < minn )
{
minn = s;
for( int i = 1; i <= minn; i++ )
{
ans[i] = temp[i];
}
}
}
return;
}
temp[s+1] = t;
dfs( t+1, s+1 );
temp[s+1] = 0;
dfs( t+1, s );
}
int main()
{
cin >> v;
for( int i = 1; i <= v; i++ )
{
cin >> need[i];
}
cin >> g;
for( int i = 1; i <= g; i++ )
{
for( int j = 1; j <= v; j++ )
{
cin >> im[i][j];
}
}
dfs( 1, 0 );
cout << minn << " ";
for( int i = 1; i <= minn; i++ )
{
cout << ans[i] << ( i == minn ? "\n" : " " );
}
return 0;
}
学习总结:
遇到组合类问题可以考虑dfs,遇到连通体或者最短路径可以考虑bfs。
//全排列
const int maxn = 2e6+5;
bool vis[maxn];
int box[maxn], n;
void put_card_into_box( int j )
{
if( j == n + 1 )
{
for( int i = 1; i <= n; i++ )
{
cout << box[i];
}
cout << endl;
return;
}
for( int i = 1; i <= n; i++ )
{
if( !vis[i] )
{
box[j] = i;
vis[i] = true;
put_card_into_box( j + 1 );
vis[i] = false;
}
}
}
//dfs
void dfs( int step )
{
//如果到达终点,计数加一,返回
if( 符合终止条件 )
{
结束递归,返回
}
//做出一个决策,进行下一步
dfs(step+1);
//撤回这个决策,进行下一步
dfs(step+1);
}
//bfs
void bfs()
queue q;
//初始状态入队
while( !q.empty() )
{
//队首出队,
if( 判断符合条件或到达边界 ) return;
//由队首拓展新状态
if(新状态合理)
{
//新状态入队
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号