寒假集训专题二：二分查找与二分答案

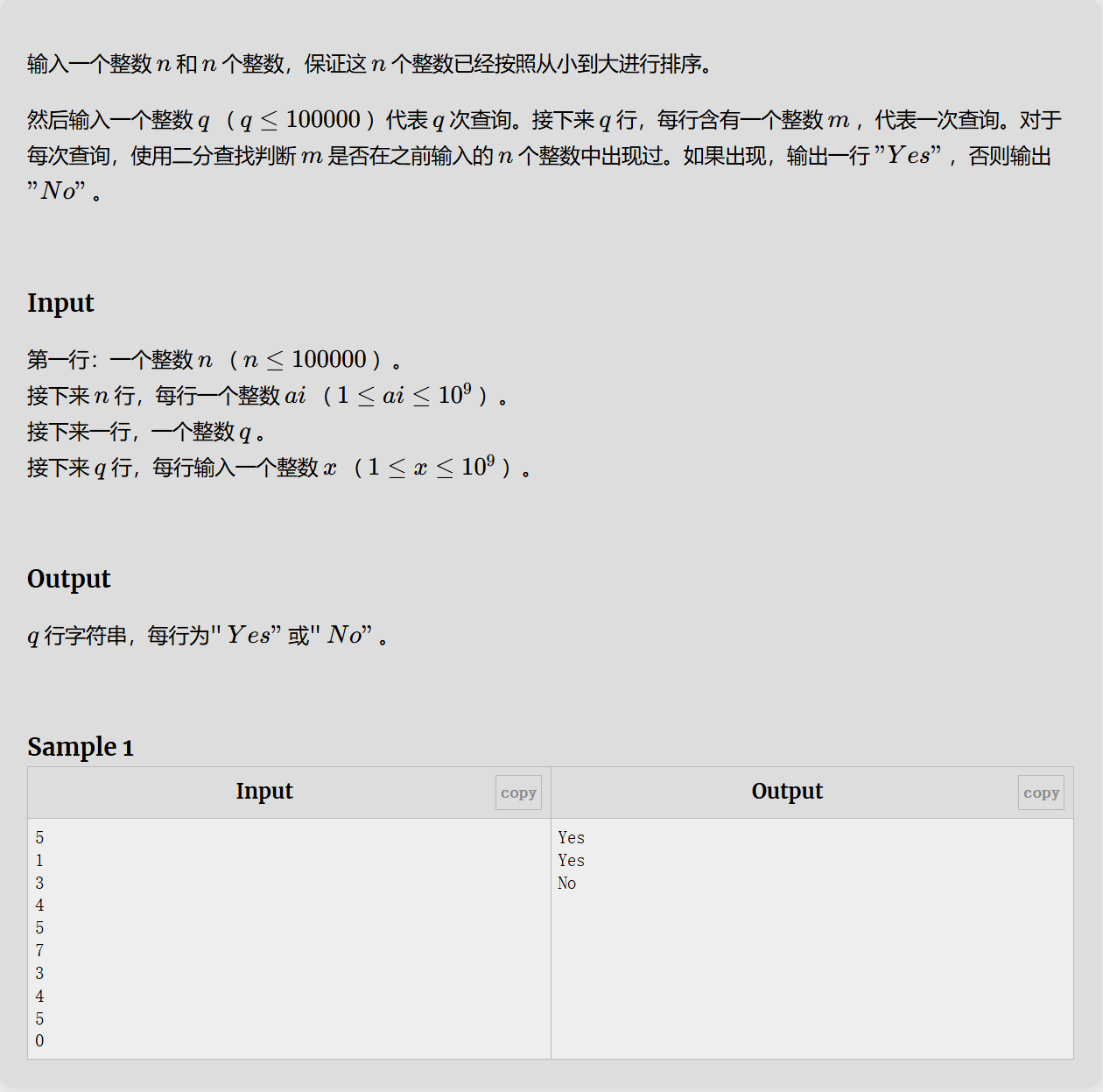
ESAY1：二分查找

解题思路：
简单的最基础的二分查找，目的是熟悉模板，套用二分查找的模板就可以快速解决了。

#include<bits/stdc++.h>
#include<vector>
#include<algorithm>
using namespace std;

//引用符号是否添加对于效率上影响较大 
bool check( int k, const vector<int>& nums )
{
	int n = nums.size();
	int l = 0, r = n - 1;
	while( l <= r )
	{
		int mid =  l + ( r - l ) / 2;
		if( k < nums[mid] )
		{
			r = mid - 1;
		}
		else if( k > nums[mid] )
		{
			l = mid + 1;
		}
		else
		{
			return true;
		}
	}
	return false;
}

int main()
{
	int n;
	cin >> n;
	vector<int> nums(n);
	for( int i = 0; i < n; i++ )
	{
		cin >> nums[i]; 
	}
	
	sort( nums.begin(), nums.end() );
	
	int q;
	cin >> q;
	while( q-- )
	{
		int x;
		cin >> x;
		if( check( x, nums ) )
		{
			cout << "Yes" << endl;
		}
		else
		{
			cout << "No" << endl;
		}
	}
	return 0;
}

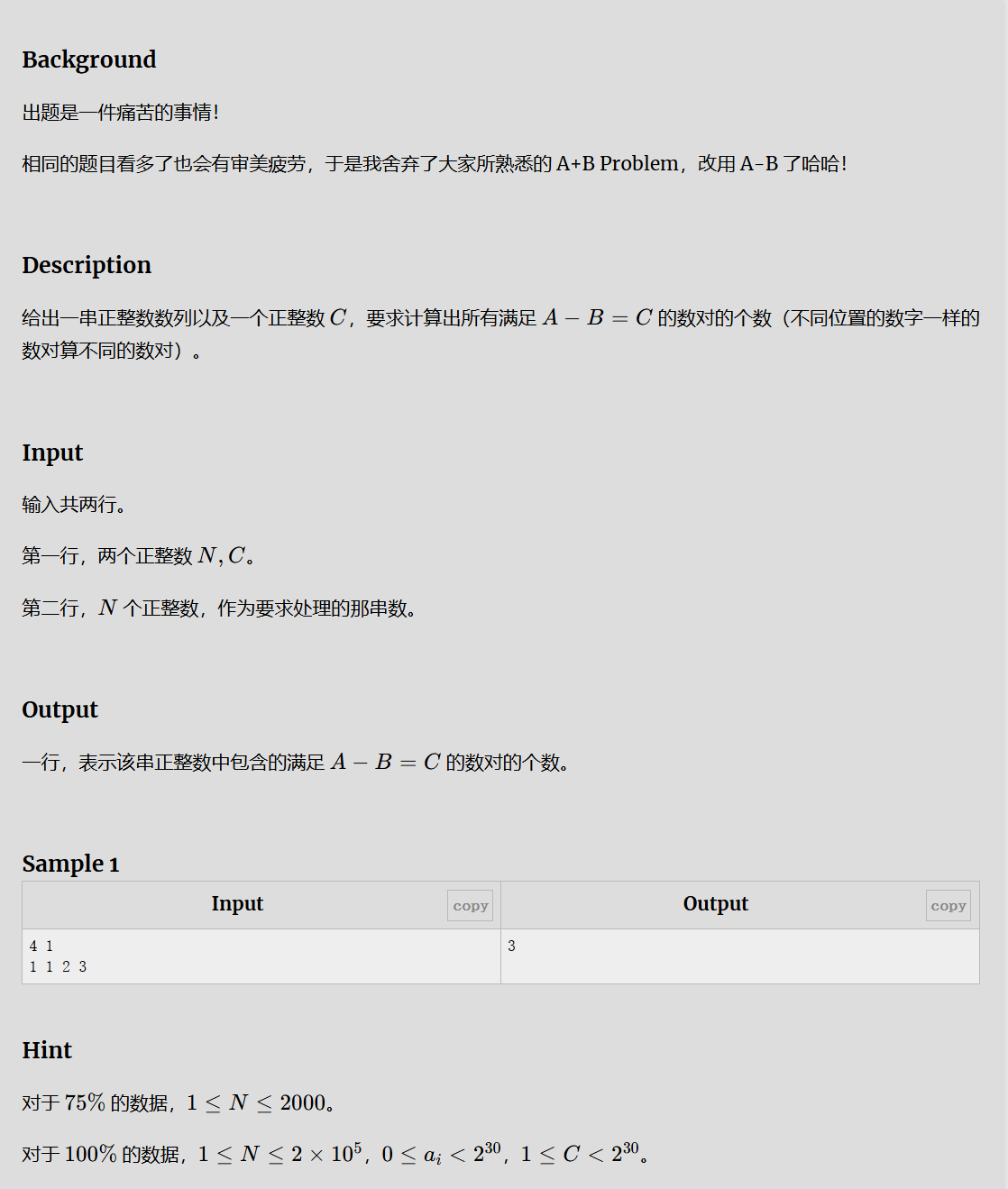
ESAY2：A-B数对

解题思路：
这道题的终止条件相较模板来说有变化，因为我们的思路是选取A-B=C中任一个A或者B，（我选择的是B）然后遍历每一个B，记录下对应的A的个数，在查找A的个数时，我们需要找到A的左右边界来获取最后需要的个数（r-l+1），所以我们的目标就不是mid，而是l和r了。
在左边界的获取中l=mid+1，r=mid，在右边界中为r=mid-1，l=mid（此时，我们的mid取值应该更靠近右侧，所以我们采取+1来进行向上的取整，防止出现死循环的情况）。判断条件也变成了差值为c。

#include<bits/stdc++.h>
#include<vector>
#include<algorithm>
using namespace std;

int main()
{
	int n;
	long long c;
	long long cnt = 0;
	cin >> n >> c;
	vector<long long> nums(n);
	for( int i = 0; i < n ; i++ )
	{
		cin >> nums[i];
	} 
	
	sort( nums.begin(), nums.end() );
	
	for( int i = 0; i < n - 1; i++ )
	{
		int l = i + 1, r = n - 1;
		//寻找左边界 
		while( l < r )
		{
			int mid = l + ( r - l ) / 2;
			if( nums[mid] - nums[i] >= c )
			{
				r = mid;
			}
			else
			{
				l = mid + 1;
			}
		}
		if( nums[l] - nums[i] == c )
		{
			int start = l;
			l = start;
			r = n - 1;
			while( l < r )
			{
				int mid = l + ( r - l + 1 ) / 2;
				if( nums[mid] - nums[i] == c )
				{
					l = mid;
				}
				else
				{
					r = mid - 1;
				}
			}
			cnt += l - start + 1;
		}
	}
	cout << cnt << endl;
	return 0;
}

MEDIUM1:分巧克力

解题思路：
这道就是运用二分答案的题目，我们在寻找尽可能大的边长在这里需要满足切割巧克力总数大于等于需要分给的小朋友人数，所以这就是我们的判断条件；右边界最大边长我们设为长宽最大值。将判断条件和边界设置套入我们的二分模板就能完成这道题的解答了。

#include<bits/stdc++.h>
#include<vector>
#include<utility>
using namespace std;

bool check( long long a, long long k, const vector<pair<long long, long long>>& chocos )
{
	long long cnt = 0;
	for( auto choco : chocos )
	{
		cnt += ( choco.first / a ) * ( choco.second / a ); 
	}
	
	return cnt >= k;
}

int main()
{
	long long n,k;
	cin >> n >> k;
	long long x = 0;
	
	vector<pair<long long, long long>>	chocos(n);
	for( long long i = 0; i < n; i++ )
	{
		long long H,W;
		cin >> H >> W;
		x = max( x, max( H, W ) );
		chocos[i] = {H, W};
	}
	
	long long l = 1, r = x, ans = 0;
	while( l <= r )
	{
		int mid = l + ( r - l ) / 2;
		if( check( mid, k, chocos ) )
		{
			l = mid + 1;
			ans = mid;	
		}
		else
		{
			r = mid - 1;	
		} 
	}
	
	cout << ans << endl;
	
	return 0;
} 

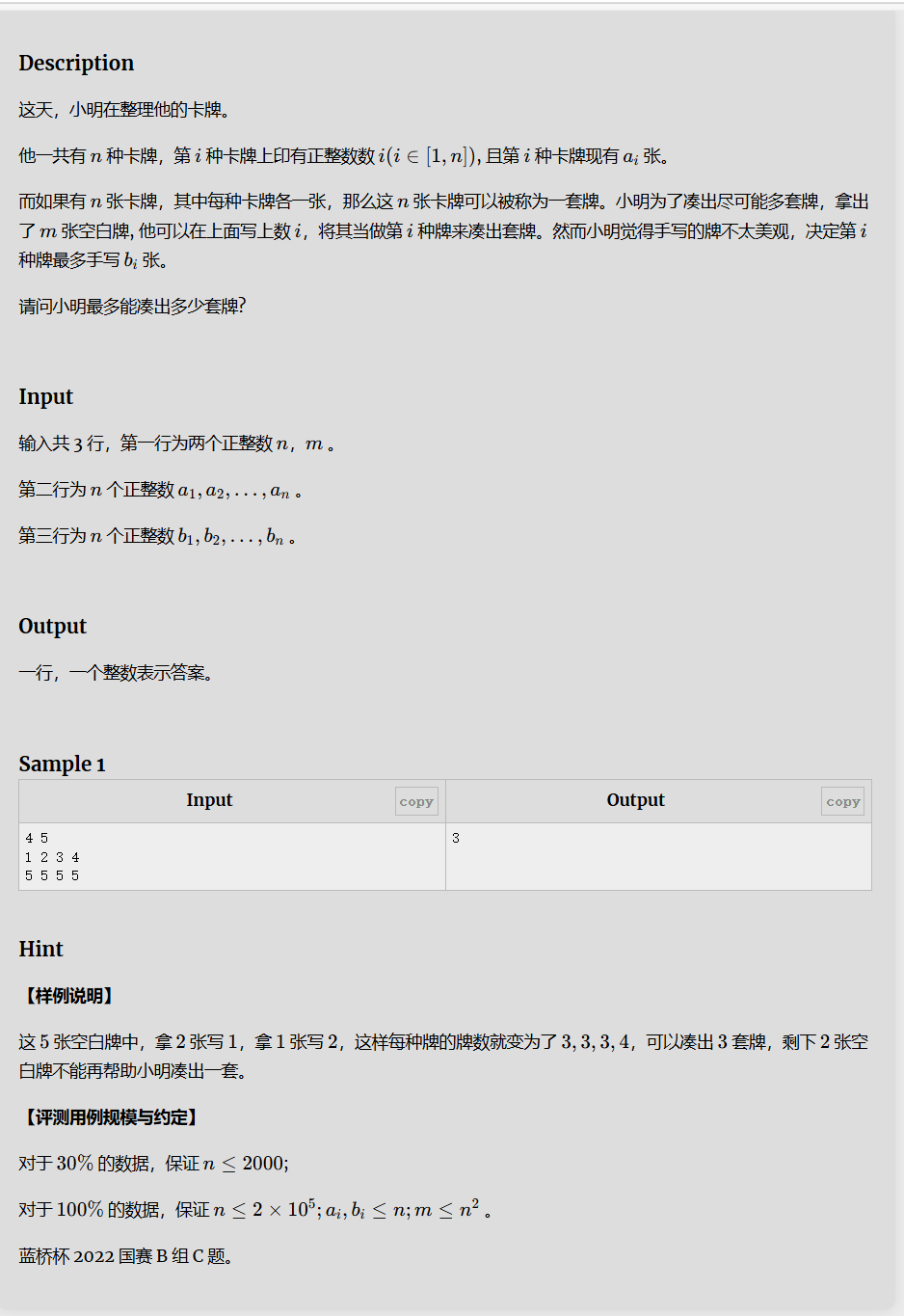
MEDIUM2：卡牌

解题思路：
这道题相对上道题目会复杂一点，我们在考虑最大套数时，可能会尽可能想多增加套数，所以我们把右边界设置为卡牌原有数量加上可补数量的最大值，以免有答案未被纳入考虑范围。左边界因为存在一套都组成不了的情况，所以我们设置为0。判断条件及我们在满足mid套牌时需要的空白牌数是否超出所给的最大数量，以及每一种牌的补牌数量是否超出补牌数量的限制。将上述考虑套入我们的二分查找模板就可以解决这道题了。

#include<bits/stdc++.h>
#include<vector>
using namespace std;
//右界没更新的问题 

bool check( long long k, long long m, vector<long long>& cards, vector<long long>& limits )
{
	long long cnt = 0;
	long long n = cards.size();
	for( long long i = 0; i < n; i++ )
	{
		long long need = k - cards[i];
		if( need > limits[i] )
		{
			return false;
		}
		else
		{
			cnt += max( need , 0LL );
		}
	}
	
	return cnt <= m;
}

int main()
{
	long long n, m;
	long long l = 0, r = n, ans = 0;
	cin >> n >> m;
	vector<long long> cards(n);
	vector<long long> limits(n);
	for( long long i = 0; i < n; i++ )
	{
		cin >> cards[i];
		l = min( l, cards[i] );
	}
	
	for( long long i = 0; i < n; i++ )
	{
		cin >> limits[i];
		r = max( r, limits[i] + cards[i] );
	}
	
	while( l <= r )
	{
		long long mid = l + ( r - l ) / 2;
		if( check( mid, m, cards, limits ) )
		{
			ans = mid;
			l = mid + 1;
		}
		else
		{
			r = mid - 1;
		}
	}
	
	cout << ans << endl;
	
	return 0; 
	
}

学习总结：

以前在做题中我通常直接使用find()来查找元素，没有重视过二分查找，所以在模板学习和理解中遇到了些许困难。
通过学习认识到了(l<r)和(l<=r)判断条件的不同使用场景，以及边界处理情况。以及见识到了hard题里面的青蛙那道题的比较奇妙的解题思路。
最基础二分模板：
while(l<r) { mid = l+(r-l)/2; if(判断mid是否合法) { ans = mid; l = mid + 1; } else { r = mid - 1; } }