Python-AVL树

 

查看代码

 class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None  # 左孩子
        self.rchild = None  # 右孩子
        self.parent = None


class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert_on_rec(val)

    def insert(self, node, val):
        """使用递归的方式插入"""
        if not node:
            node = BiTreeNode(val)
        elif val < node.data:
            node.lchild = self.insert(node.lchild, val)
            node.lchild.parent = node
        elif val > node.data:
            node.rchild = self.insert(node.rchild, val)
            node.rchile.parent = node
        return node

    def insert_on_rec(self, val):
        # 非递归插入
        p = self.root
        if not p:  # 空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:  # 左孩子不存在
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return

    def query(self, node, val):
        """递归查询"""
        if not node:
            return None
        if node.data < val:
            return self.query(node.rchild, val)
        elif node.data > val:
            return self.query(node.lchild, val)
        else:
            return node

    def query_no_rec(self, val):
        """非查询递归"""
        p = self.root
        while p:
            if p.data < val:
                p = p.rchild
            elif p.data > val:
                p = p.lchild
            else:
                return p
        return None

    def pre_order(self, root):  # 前序遍历
        if root:
            print(root.data, end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)

    def in_order(self, root):  # 中序遍历
        if root:
            self.in_order(root.lchild)
            print(root.data, end=',')
            self.in_order(root.rchild)

    def post_order(self, root):  # 后序遍历
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=',')


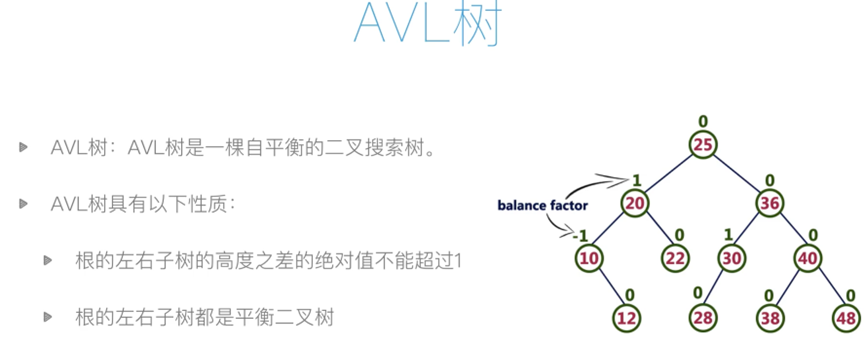
class AVLNode(BiTreeNode):
    def __init__(self, data):
        BiTreeNode.__init__(self, data)
        self.bf = 0


class AVLTree(BST):
    def __init__(self, li=None):
        BST.__init__(self, li)

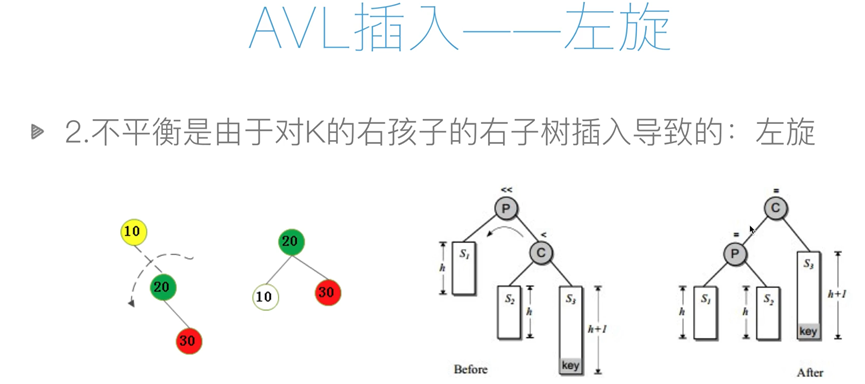
    def rotate_left(self, p, c):  # 左旋
        s2 = c.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        c.lchild = p
        p.parent = c
        p.bf = 0
        c.bf = 0
        return c

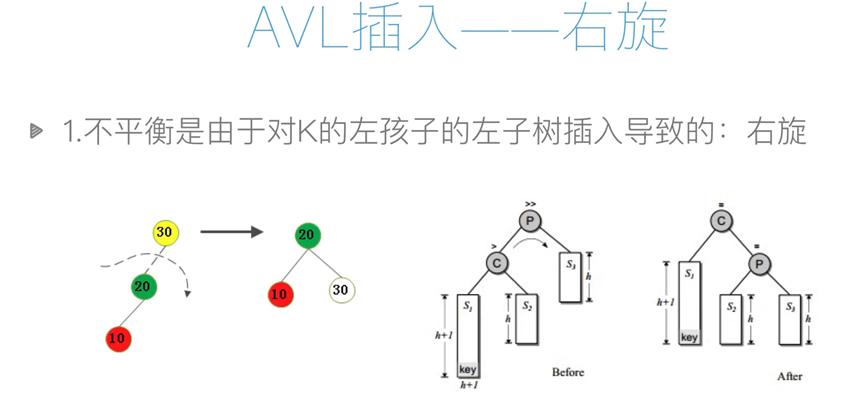
    def rotate_right(self, p, c):  # 右旋
        s2 = c.rchild
        p.lchild = s2
        if s2:
            s2.parent = p

        c.rchild = p
        p.parent = c

        p.bf = 0
        c.bf = 0
        return c

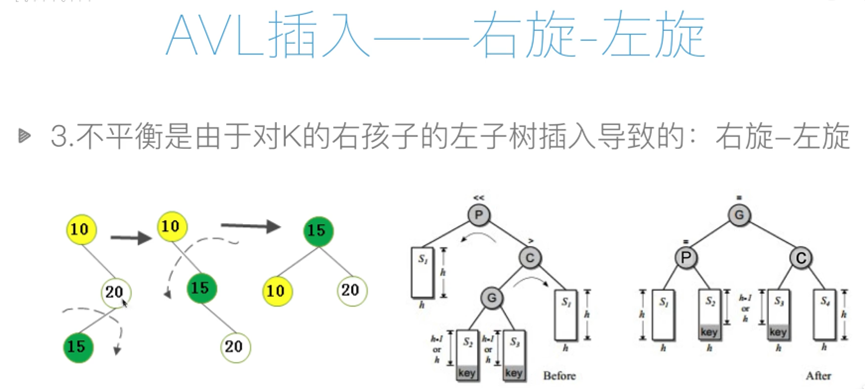
    def rotate_right_left(self, p, c):  # 右旋-左旋
        g = c.lchild
        s3 = g.rchild
        c.lchild = s3
        if s3:
            s3.parent = c
        g.rchild = c
        c.parent = g

        s2 = g.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        g.lchild = p
        p.parent = g

        # 更新bf
        if g.bf > 0:
            p.bf = -1
            c.bf = 0
        elif g.bf < 0:
            p.bf = 0
            c.bf = 1
        else:  # 插入的是g
            p.bf = 0
            c.bf = 0
        g.bf = 0
        return g

    def rotate_left_right(self, p, c):  # 左旋-右旋
        g = c.rchild
        s2 = g.lchild
        c.rchild = s2
        if s2:
            s2.parent = c
        g.lchild = c
        c.parent = g

        s3 = g.rchild
        p.lchild = s3
        if s3:
            s3.parent = p
        g.rchild = p
        p.parent = g

        # 更新bf
        if g.bf < 0:
            p.bf = 1
            c.bf = 0
        elif g.bf > 0:
            p.bf = 0
            c.bf = -1
        else:
            p.bf = 0
            c.bf = 1
        g.bf = 0
        return g

    def insert_on_rec(self, val):
        # 1. 和BST一样，插入
        p = self.root
        if not p:  # 空树
            self.root = AVLNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:  # 左孩子不存在
                    p.lchild = AVLNode(val)
                    p.lchild.parent = p
                    node = p.lchild  # node 存储的就是插入的节点
                    break
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = AVLNode(val)
                    p.rchild.parent = p
                    node = p.rchild
                    break
            else:  # val == p.data
                return

        # 2. 更新balance factor
        while node.parent:  # node.parent不空
            if node.parent.lchild == node:  # 传递是从左子树，左子树更沉了
                # 更新node.parent和bf -= 1
                if node.parent.bf < 0:  # 原来node.parent.bf == -1，更新后变成-2
                    # 做旋转
                    # 看node哪边沉
                    g = node.parent.parent  # 为了连接旋转之后的子树
                    x = node.parent  # 旋转前的字数的根
                    if node.bf > 0:
                        n = self.rotate_left_right(node.parent, node)
                    else:
                        n = self.rotate_right(node.parent, node)
                    # 记得：把n和g连起来
                elif node.parent.bf > 0:  # 原来node.parent.bf == 1，更新后变成0
                    node.parent.bf = 0
                    break
                else:  # 原来node.parent.bf == 0，更新后变成-1
                    node.parent.bf = -1
                    node = node.parent
                    continue
            else:  # 传递是从右子树来的，右子树更沉了
                # 更新node.parent.bf += 1
                if node.parent.bf > 0:  # 原来node.parent.bf == 1，更新后变成2
                    # 做旋转
                    # 看node哪边沉
                    g = node.parent.bf  # 为了连接旋转之后的子树
                    x = node.parent  # 旋转前的字数的根
                    if node.bf < 0:  # node.bf = 1
                        n = self.rotate_right_left(node.parent, node)
                    else:  # node.bf = -1
                        n = self.rotate_left(node.parent, node)
                    # 记得连起来
                elif node.parent.bf < 0:  # 原来node.parent.bf == -1，更新后变成0
                    node.parent.bf = 0
                    break
                else:  # 原来node.parent.bf == 0，更新后变成1
                    node.parent.bf = 1
                    node = node.parent
                    continue
            # 连接旋转后的子树
            n.parent = g
            if g:  # g不是空
                if x == g.lchild:
                    g.lchild = n
                else:
                    g.rchild = n
                break
            else:
                self.root = n
                break


tree = AVLTree([9, 8, 7, 6, 5, 4, 3, 2, 1])
tree.pre_order(tree.root)
print("")
tree.in_order(tree.root)