机器学习笔记:朴素贝叶斯及贝叶斯网络
-
朴素贝叶斯(Naïve Bayes)
-
贝叶斯基础知识
众所周知,朴素贝叶斯是一种简单但是非常强大的线性分类器。它在垃圾邮件处理、文档分类、疾病诊断(糖尿病诊断)等方面中都取得了很大的成功。它之所以称为朴素,是因为它假设特征之间是相互独立的。但是在现实生活中,这种假设基本上是不成立的。那么即使是在假设不成立的条件下,它依然表现的很好,尤其是在小规模样本的情况下。但是如果每个特征之间有很强的关联性和非线性的分类问题使用朴素贝叶斯会有很差的分类效果
贝叶斯公式:
![]()
①后验概率(Posterior Probabilities)
![]() 是后验概率,一般是我们求解的目标,在x发生的条件下Y发生的概率。
是后验概率,一般是我们求解的目标,在x发生的条件下Y发生的概率。 ②先验概率(Prior Probabilities)
![]() 、
、![]() 是先验概率,根据以往经验和分析得到的概率,统计得到
是先验概率,根据以往经验和分析得到的概率,统计得到 ③似然概率(也叫条件概率)
![]() 一般是通过历史数据统计得到
一般是通过历史数据统计得到 ④条件概率的公式:
![]()
即事件A和事件B同时发生的概率等于在A发生的条件下B发生的概率乘以A的概率。
⑤全概率公式:
假设B是由相互独立的事件组成的概率空间
![]() ,则
,则![]() 可以用全概率公式展开:
可以用全概率公式展开: ![]()
-
⑥举例:
某个医院早上收了六个门诊病人,如下表:
症状 职业 疾病
打喷嚏 护士 感冒
打喷嚏 农夫 过敏
头痛 建筑工人 脑震荡
头痛 建筑工人 感冒
打喷嚏 教师 感冒
头痛 教师 脑震荡现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
根据贝叶斯定理:
P(A|B) = P(B|A) P(A) / P(B)
可得
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏x建筑工人|感冒) x P(感冒)
/ P(打喷嚏x建筑工人)假定"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
/ P(打喷嚏) x P(建筑工人)这是可以计算的。
P(感冒|打喷嚏x建筑工人)
= 0.66 x 0.33 x 0.5 / 0.5 x 0.33
= 0.66因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率(这里这两个概率都为0值)。比较这几个概率,就可以知道他最可能得什么病。
其实这个例子已经开始分类了,是否患病,患哪种病,只不过都是概率的形式来描述
-
模型概述
朴素贝叶斯方法,是指:
朴素:特征条件独立
贝叶斯:基于贝叶斯定理
根据贝叶斯定理,对于一个分类问题,给定样本特征x,样本属于类别y的概率是
![]()
在这里,x是一个特征向量,将x维度设为M,因为朴素的假设,即特征条件独立,根据全概率公式展开,公式(1)可表达为:
![]()
这里,只要分别估计出,特征
![]() 在每一类的条件概率就可以了,类别y的先验概率可以通过训练集算出,同样通过训练集上的统计,可以得出对应每一类上的,条件独立的特征对应的条件概率向量。
在每一类的条件概率就可以了,类别y的先验概率可以通过训练集算出,同样通过训练集上的统计,可以得出对应每一类上的,条件独立的特征对应的条件概率向量。
-
学习贝叶斯模型
训练集
![]() 包含N条训练数据,其中
包含N条训练数据,其中![]() 是M维向量,
是M维向量,![]() 属于K类中的一类。
属于K类中的一类。
❶学习1: 统计训练集中
![]() 的数目,然后除以总的训练样本数目得到
的数目,然后除以总的训练样本数目得到![]() 的概率
的概率
![]()
❷学习2:
![]()
经过上述步骤,我们就得到了模型的基本概率,也就完成了学习的任务。
-
使用贝叶斯模型进行分类
![]()
-
拉普拉斯平滑
![]()
-
朴素贝叶斯实现文本分类常见模型
❶文本分类问题
在文本分类中,假设我们有一个文档d∈X,X是文档向量空间(document space),和一个固定的类集合C={c1,c2,…,cj},类别又称为标签。显然,文档向量空间是一个高维度空间。我们把一堆打了标签的文档集合& lt;d,c>作为训练样本,∈X×C。例如:
={Beijing joins the World Trade Organization, China}
对于这个只有一句话的文档,我们把它归类到 China,即打上china标签。
我们期望用某种训练算法,训练出一个函数γ,能够将文档映射到某一个类别:
γ:X→C
这种类型的学习方法叫做有监督学习,因为事先有一个监督者(我们事先给出了一堆打好标签的文档)像个老师一样监督着整个学习过程。
朴素贝叶斯分类器是一种有监督学习,常见有两种模型,多项式模型(multinomial model)和伯努利模型(Bernoulli model)。
❷多项式模型
基本原理:在多项式模型中,设文档
![]() ,整个文档的单词顺序就是d,
,整个文档的单词顺序就是d,![]() 是该文档中出现过的单词,允许重复,c为文档的种类。则先验概率
是该文档中出现过的单词,允许重复,c为文档的种类。则先验概率![]()
![]()
V是训练样本的单词表(即抽取单词,单词出现多次,只算一个),|V|则表示训练样本包含多少种单词。在这里,m=|V|, p=1/|V|。
P(tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据,而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。
-
-
贝叶斯网络
-
贝叶斯定理:
![]()
-
贝叶斯网络
-
贝叶斯网络的定义
贝叶斯网络(Bayesian network),又称信念网络(Belief Network),或有向无环图模型(directed acyclic graphical model),是一种概率图模型,于1985年由Judea Pearl首先提出,它是一种模拟人类推理过程中因果关系的不确定性处理模型,其网络拓扑结构是一个有向无环图(DAG)。
贝叶斯网络的有向无环图中的节点表示随机变量
![]() ,他们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是"因(parents)",另一个是"果(children)",两节点就会产生一个条件概率值。
,他们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是"因(parents)",另一个是"果(children)",两节点就会产生一个条件概率值。
总而言之,连接两个节点的箭头代表此两个随机变量是具有因果关系,或非条件独立。
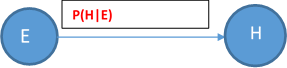
例如,假设节点E直接影响到节点H,即E->H,则用从E指向H的箭头建立节点E到节点H的有向弧(E,H),权值(即连接强度)用条件概率
![]() 来表示,如下图所示:
来表示,如下图所示:
![]()
简言之,把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖,用圈表示随机变量(random variables),用箭头表示条件依赖(conditional dependencies)。
令G=(I,E)表示一个有向无环图(DAG),其中I代表图形中所有的节点的集合,而E代表有向连接线段的集合,且令
![]() 为其有向无环图中的某一节点i所代表的随机变量,若节点X的联合概率可以表示成:
为其有向无环图中的某一节点i所代表的随机变量,若节点X的联合概率可以表示成:
![]()
则称X为相对于一有向无环图G的贝叶斯网络,其中
![]() 表示节点i之"因
表示节点i之"因
,或称
![]() 是i的父母parents。此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
是i的父母parents。此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
![]()
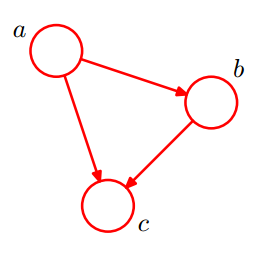
如下图,便是一个简单的贝叶斯网络:
![]()
由上图
![]() ,
,![]() 等于所有随机变量
等于所有随机变量![]() 的条件概率的乘积,即上边所说,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出。上式
的条件概率的乘积,即上边所说,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出。上式![]() ,其中
,其中![]() 的条件概率为
的条件概率为![]() ,
,![]() 的条件概率为
的条件概率为![]() ,
,![]() 的条件概率为
的条件概率为![]() 。
。
-
贝叶斯网络的3中结构形式
给定如下图的一个贝叶斯网络:
![]()
从图中可以比较直观的看出:
❶
![]() 的联合分布为:
的联合分布为:
![]()
❷
![]() 相互独立(对应head-to-head),无相互依赖关系
相互独立(对应head-to-head),无相互依赖关系
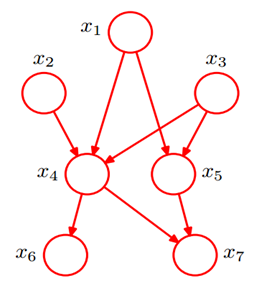
❸
![]() 在
在![]() 给定的条件下,是相互独立的。
给定的条件下,是相互独立的。
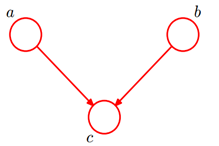
形式1:head-to-head
贝叶斯网络的第一种结构形式如下图所示:
![]()
所以有
![]() ,化简后可得:
,化简后可得:
![]()
所以最后可得:
![]()
即在c未知得条件下,a,b被阻断(blocked),是独立得,称之为head-to-head条件独立。
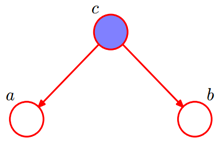
形式2:tail-to-tail
贝叶斯网络得第二种结构如下图所示:
![]()
①在c未知得条件下,有:
![]() 此时,无法得出
此时,无法得出![]() ,即c未知时,a,b不独立。
,即c未知时,a,b不独立。
②在c已知得条件下,有:
![]() ,然后将
,然后将![]() 带入式子中,得到
带入式子中,得到![]() ,即c已知时,a,b独立。
,即c已知时,a,b独立。
所以在c给定得条件下,a,b时被阻断(blocked)的,是独立的,称之为tail-to-tail条件独立。
![]()
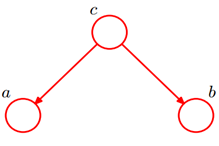
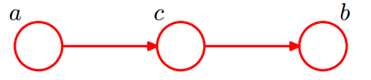
形式3:head-to-tail
贝叶斯网络的第三种结构形式如下图所示:
![]()
还是分c未知和c已知两种情况:
①、c未知时,有:
![]() ,但无法推出
,但无法推出![]() ,即c未知时,a,b不独立
,即c未知时,a,b不独立②c已知时,有:
![]()
所以在c给定的条件下,a,b被阻断(blocked),是独立的,称之为head-to-tail条件独立。
![]()
实心圆圈表示已知
根据之前对head-to-tail的讲解,我们已经知道,在xi给定的条件下,xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢?意味着:xi+1的分布状态只和xi有关,和其他变量条件独立。通俗点说,当前状态只跟上一状态有关,跟上上或上上之前的状态无关。这种顺次演变的随机过程,就叫做马尔科夫链(Markov chain)。且有:
![]()
接着,将上述结点推广到结点集,则是:对于任意的结点集A,B,C,考察所有通过A中任意结点到B中任意结点的路径,若要求A,B条件独立,则需要所有的路径都被阻断(blocked),即满足下列两个前提之一:
A和B的"head-to-tail型"和"tail-to-tail型"路径都通过C;
A和B的"head-to-head型"路径不通过C以及C的子孙;
-
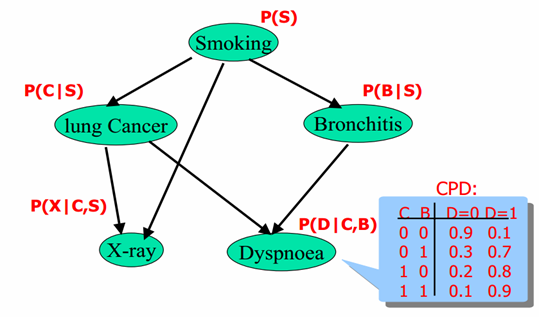
贝叶斯网络实例:
![]()
-
-


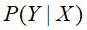

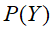 是先验概率,根据以往经验和分析得到的概率,统计得到
是先验概率,根据以往经验和分析得到的概率,统计得到 
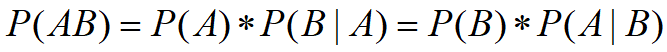
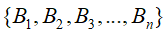 ,则
,则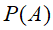 可以用全概率公式展开:
可以用全概率公式展开: 
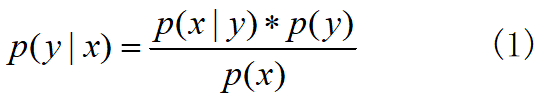

 在每一类的条件概率就可以了,类别y的先验概率可以通过训练集算出,同样通过训练集上的统计,可以得出对应每一类上的,条件独立的特征对应的条件概率向量。
在每一类的条件概率就可以了,类别y的先验概率可以通过训练集算出,同样通过训练集上的统计,可以得出对应每一类上的,条件独立的特征对应的条件概率向量。
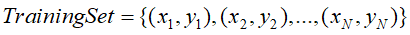 包含N条训练数据,其中
包含N条训练数据,其中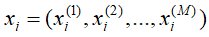 是M维向量,
是M维向量,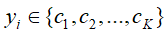 属于K类中的一类。
属于K类中的一类。
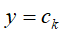 的数目,然后除以总的训练样本数目得到
的数目,然后除以总的训练样本数目得到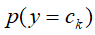 的概率
的概率




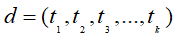 ,整个文档的单词顺序就是d,
,整个文档的单词顺序就是d,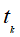 是该文档中出现过的单词,允许重复,c为文档的种类。则先验概率
是该文档中出现过的单词,允许重复,c为文档的种类。则先验概率

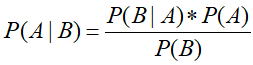
 ,他们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是"因(parents)",另一个是"果(children)",两节点就会产生一个条件概率值。
,他们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是"因(parents)",另一个是"果(children)",两节点就会产生一个条件概率值。
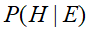 来表示,如下图所示:
来表示,如下图所示:
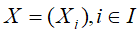 为其有向无环图中的某一节点i所代表的随机变量,若节点X的联合概率可以表示成:
为其有向无环图中的某一节点i所代表的随机变量,若节点X的联合概率可以表示成:
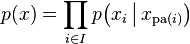
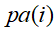 表示节点i之"因
表示节点i之"因
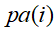 是i的父母parents。此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
是i的父母parents。此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
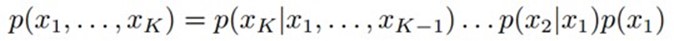
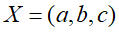 ,
,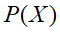 等于所有随机变量
等于所有随机变量 的条件概率的乘积,即上边所说,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出。上式
的条件概率的乘积,即上边所说,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出。上式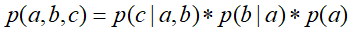 ,其中
,其中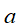 的条件概率为
的条件概率为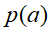 ,
,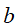 的条件概率为
的条件概率为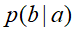 ,
,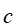 的条件概率为
的条件概率为 。
。
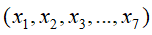
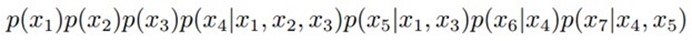
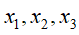
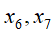
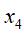 给定的条件下,是相互独立的。
给定的条件下,是相互独立的。

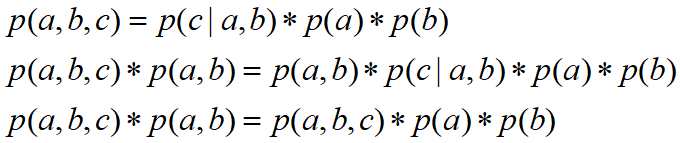
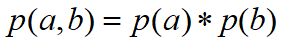
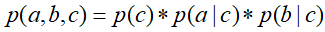 此时,无法得出
此时,无法得出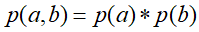 ,即c未知时,a,b不独立。
,即c未知时,a,b不独立。
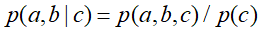 ,然后将
,然后将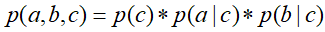 带入式子中,得到
带入式子中,得到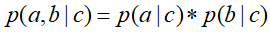 ,即c已知时,a,b独立。
,即c已知时,a,b独立。
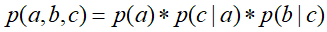 ,但无法推出
,但无法推出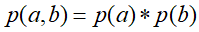 ,即c未知时,a,b不独立
,即c未知时,a,b不独立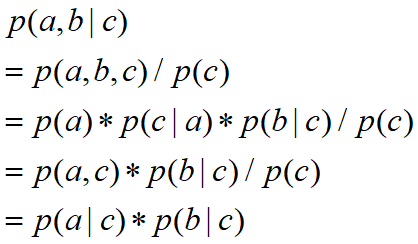



 浙公网安备 33010602011771号
浙公网安备 33010602011771号