深度学习01-(深度学习概述、感知机、神经网络、损失函数与梯度下降、反向传播算法、卷积神经网络理论）

深度学习-01

深度学习-01

深度学习-01

深度学习概述

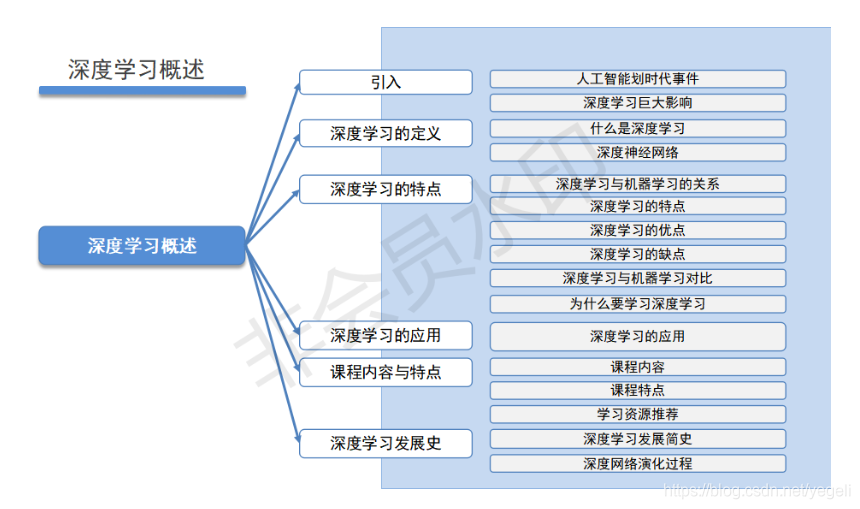
在这里插入图片描述

引入

人工智能划时代事件

在这里插入图片描述

深度学习巨大影响

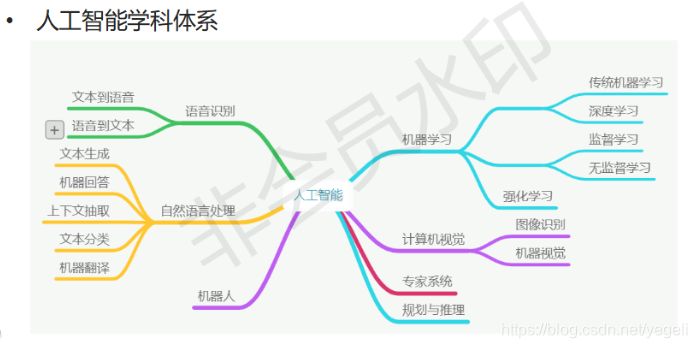
在这里插入图片描述

深度学习

什么是深度学习

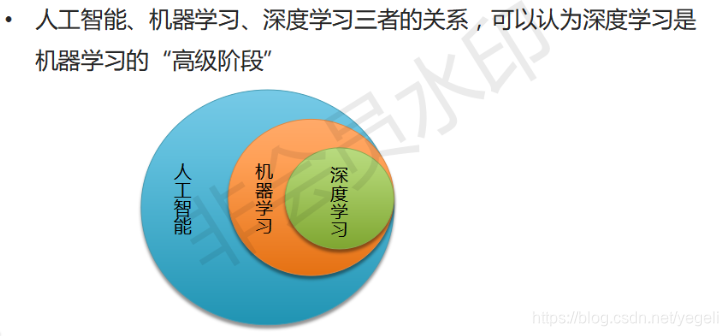
在这里插入图片描述

深度神经网络

在这里插入图片描述

深度学习与机器学习的关系

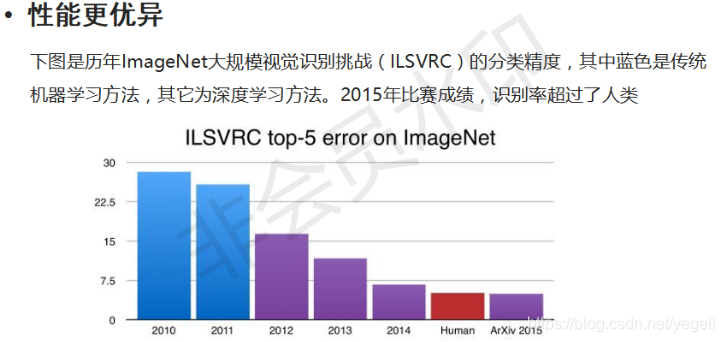
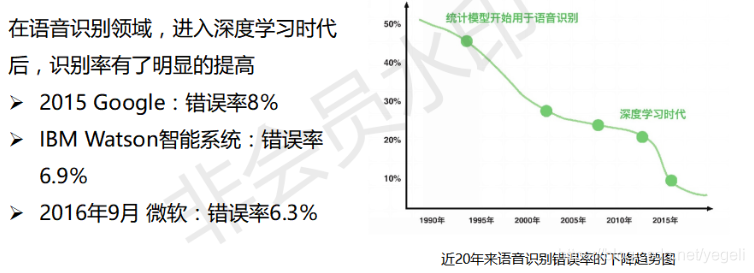
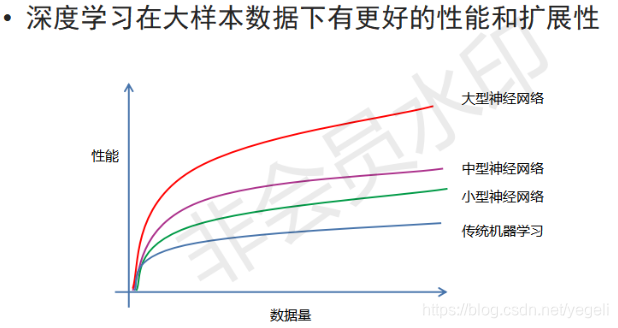
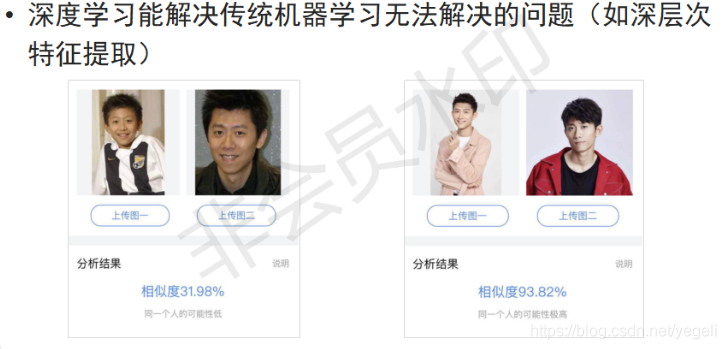
在这里插入图片描述

深度学习的特点

在这里插入图片描述

深度学习的优点

在这里插入图片描述

深度学习的缺点

在这里插入图片描述

为什么要学习深度学习

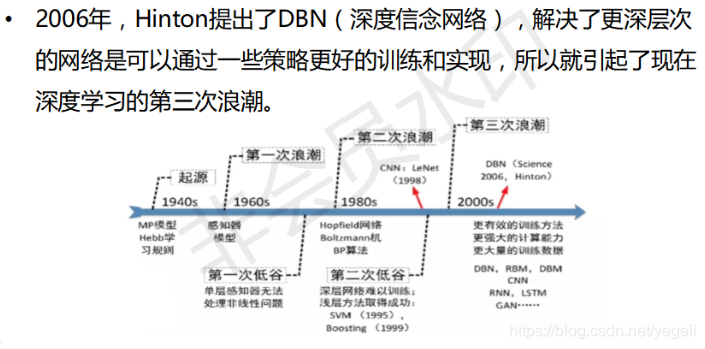
在这里插入图片描述

深度学习的应用

在这里插入图片描述

深度学习发展史

在这里插入图片描述

深度网络进化过程

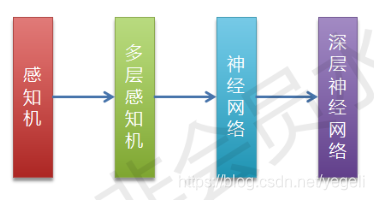
在这里插入图片描述

小结

在这里插入图片描述

感知机与神经网络

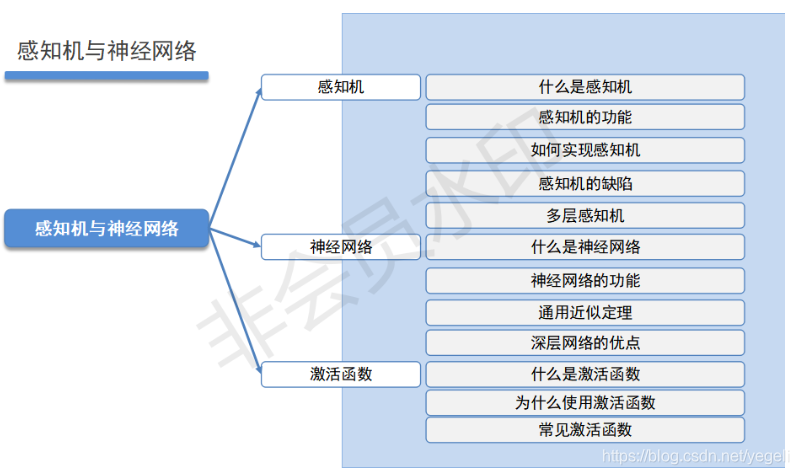
在这里插入图片描述

感知机

什么是感知机

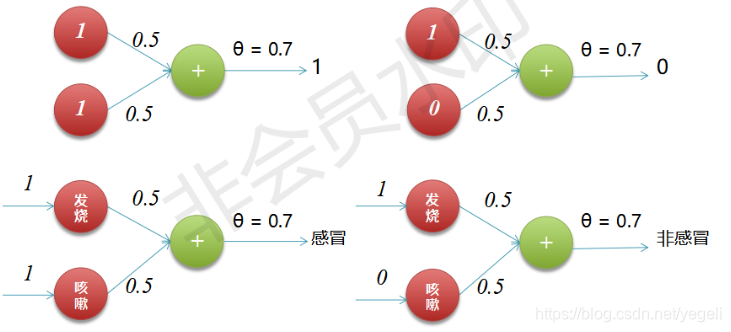
在这里插入图片描述

感知机的功能

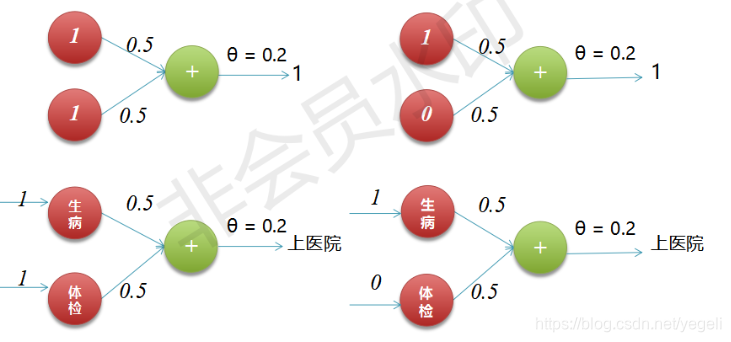
在这里插入图片描述

实现逻辑和

在这里插入图片描述

实现逻辑或

在这里插入图片描述

如何实现感知机

实现逻辑和

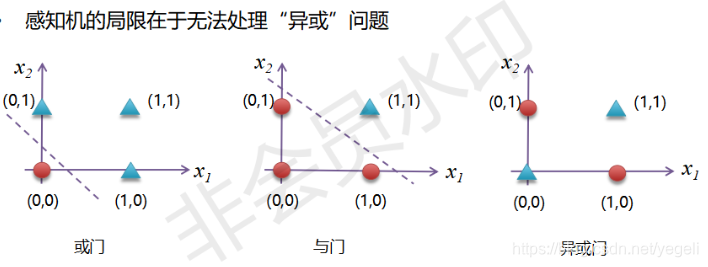
在这里插入图片描述

实现逻辑或

在这里插入图片描述

感知机的缺陷

在这里插入图片描述

多层感知机

在这里插入图片描述

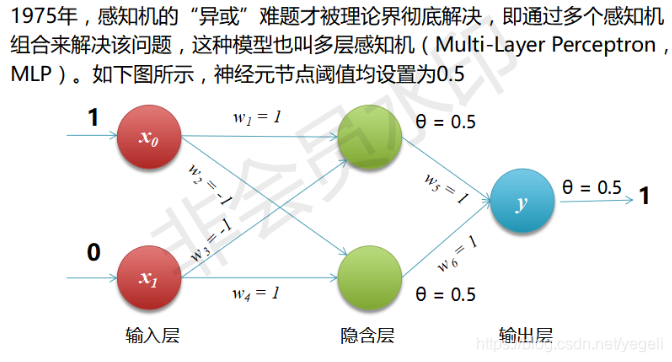
多层感知机解决异或门实现

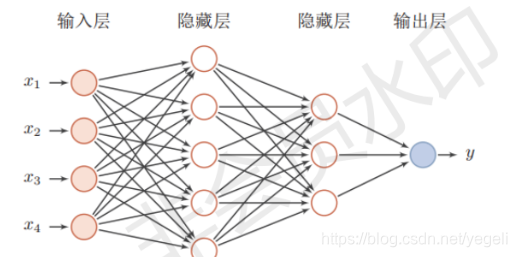
在这里插入图片描述

神经网络

什么是神经网络

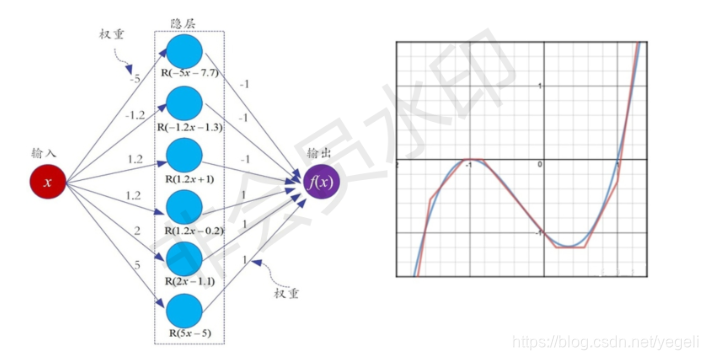
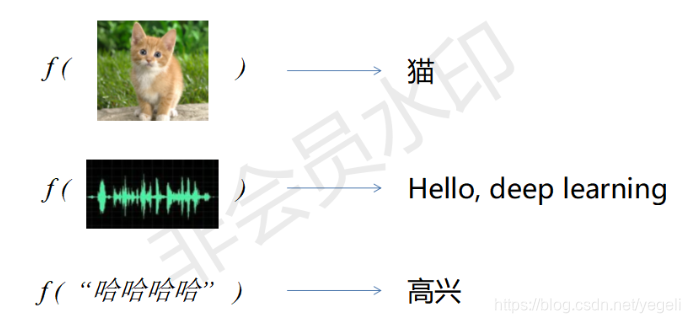
在这里插入图片描述

神经网络的功能

在这里插入图片描述

通用近似定理

在这里插入图片描述

深层网络的优点

在这里插入图片描述

激活函数

什么是激活函数

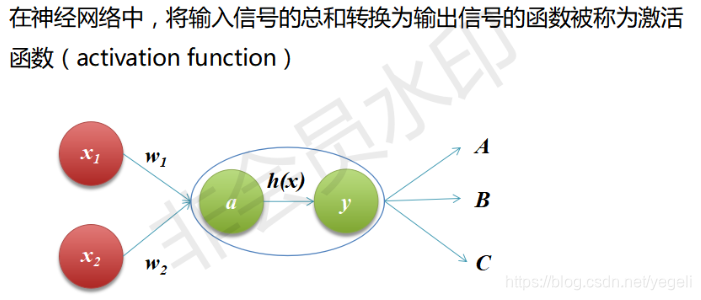
在这里插入图片描述

为什么使用激活函数

在这里插入图片描述

常见的激活函数

阶跃函数

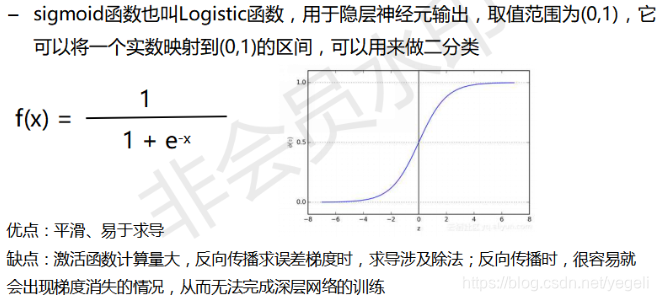
在这里插入图片描述

sigmoid函数

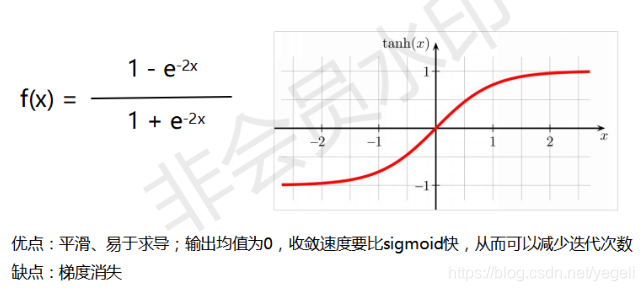
在这里插入图片描述

tanh双曲正切函数

在这里插入图片描述

ReLU(Rectified Linear Units,修正线性单元)

在这里插入图片描述

Softmax

在这里插入图片描述

小结

在这里插入图片描述

损失函数与梯度下降

在这里插入图片描述

损失函数

什么是损失函数

在这里插入图片描述

损失函数的作用

在这里插入图片描述

常用的损失函数

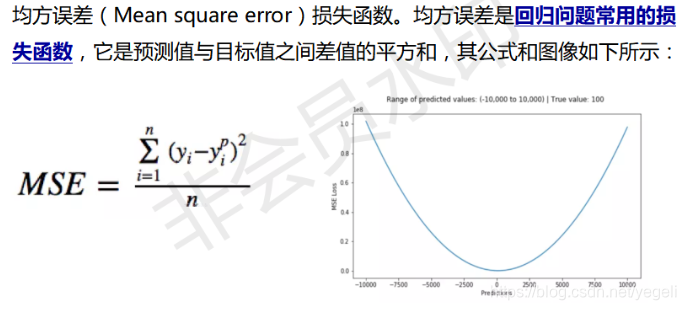
均方误差损失函数

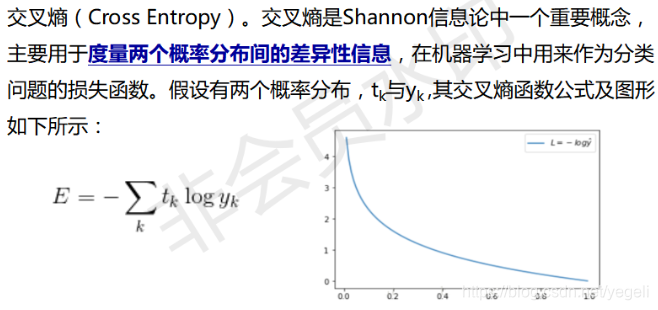
在这里插入图片描述

交叉熵

在这里插入图片描述

梯度下降

什么是梯度下降

在这里插入图片描述

梯度下降

在这里插入图片描述

导数与偏导数

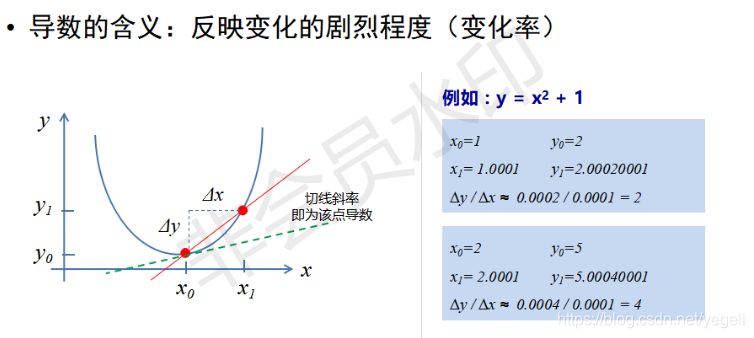
导数

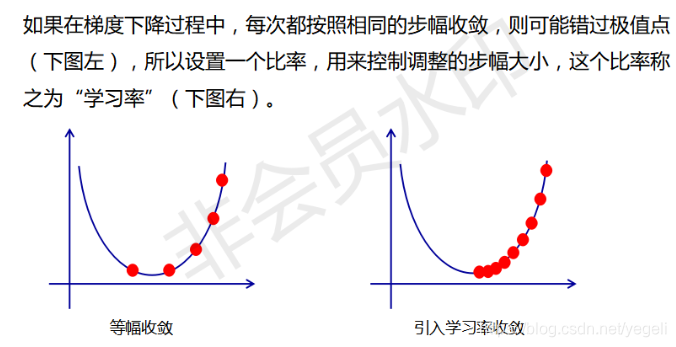
在这里插入图片描述

偏导数

在这里插入图片描述

学习率

在这里插入图片描述

梯度递减训练法则

在这里插入图片描述

梯度下降算法

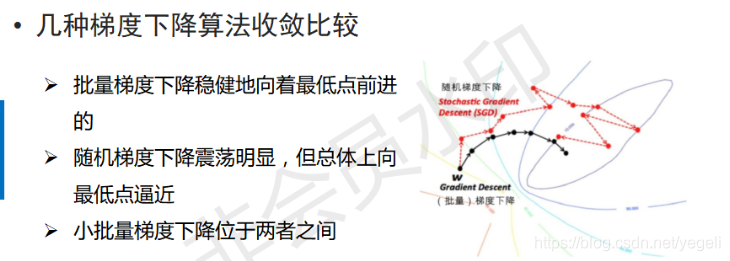
批量梯度下降

在这里插入图片描述

随机梯度下降

在这里插入图片描述

小批量梯度下降

在这里插入图片描述

几种梯度下降算法收敛比较

在这里插入图片描述

小结

在这里插入图片描述

反向传播算法

在这里插入图片描述

什么是正向传播网络

在这里插入图片描述

什么是反向传播

在这里插入图片描述

为什么需要反向传播

在这里插入图片描述

反向传播算法及简史

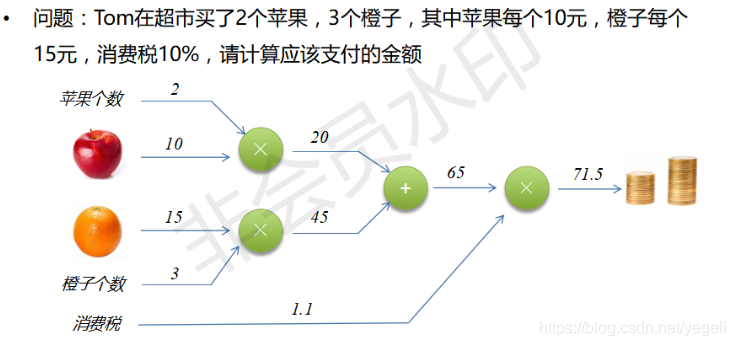
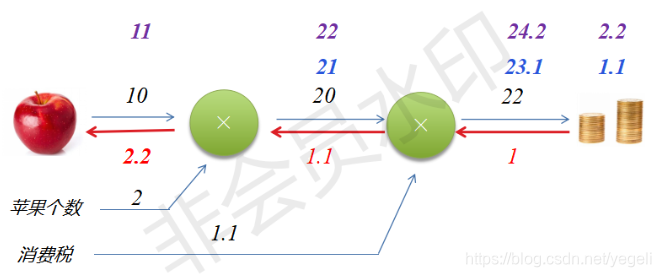
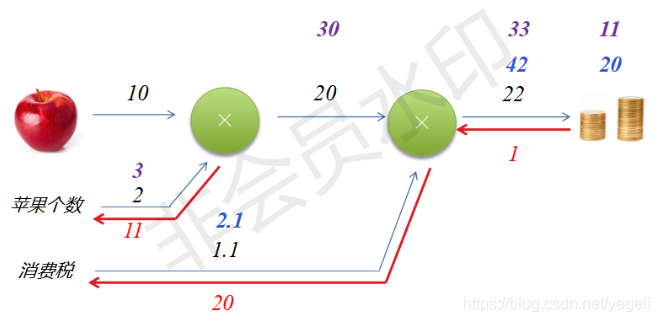
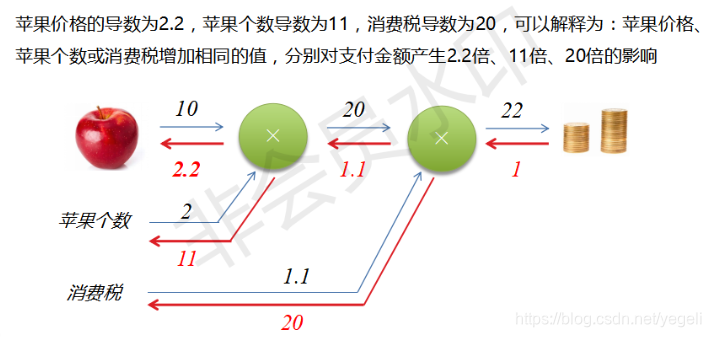
在这里插入图片描述

图解反向传播

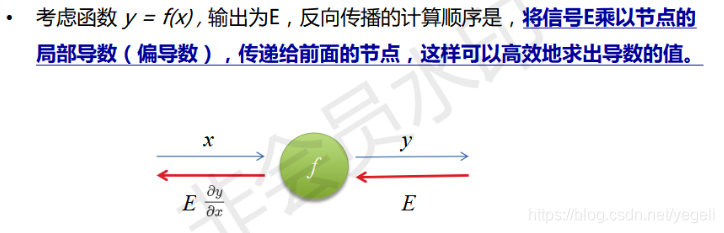
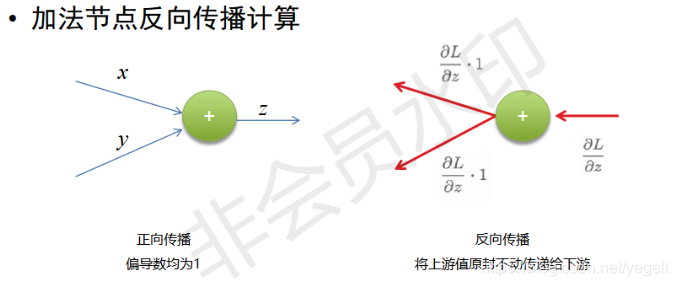
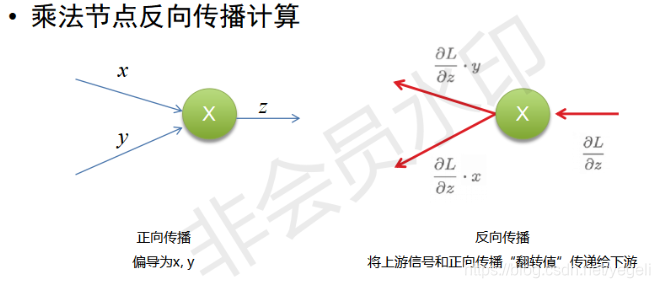
在这里插入图片描述

反向传播计算

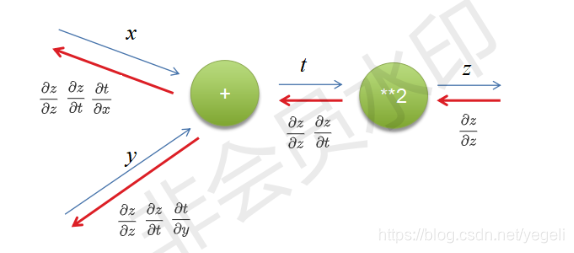
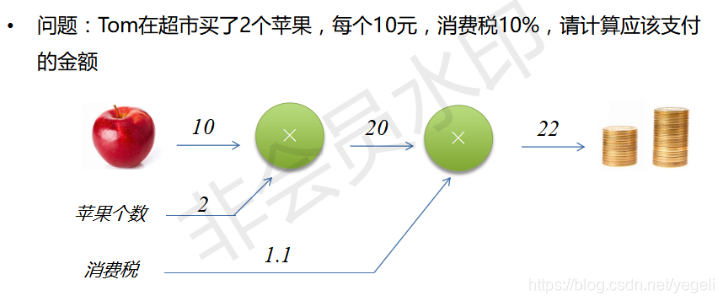
在这里插入图片描述

链式求导法则

在这里插入图片描述

案例1：通过反向传播计算偏导数

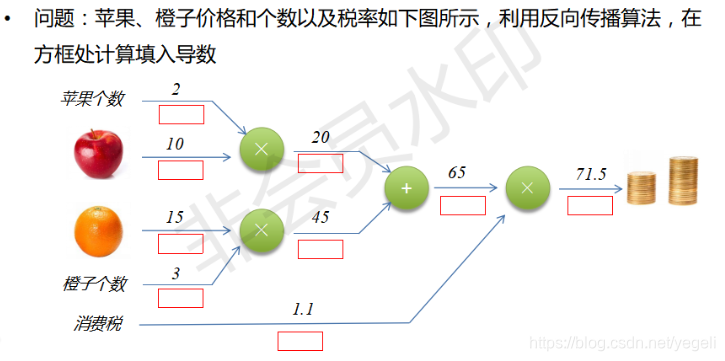
在这里插入图片描述

小结

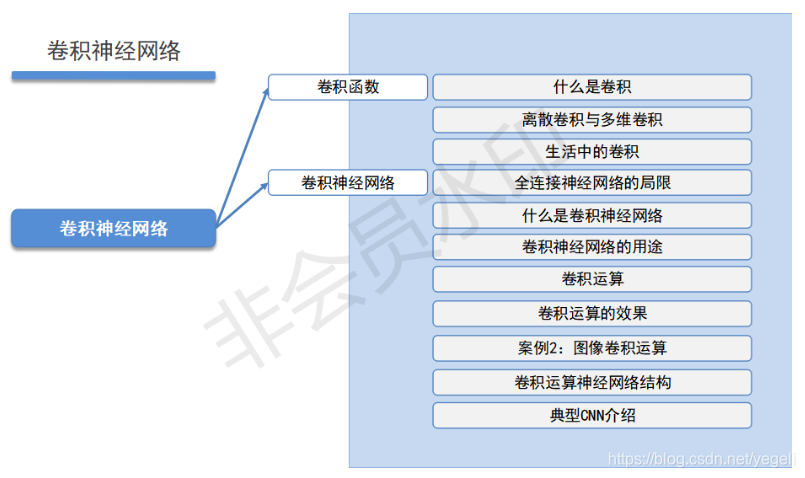
在这里插入图片描述

卷积神经网络

在这里插入图片描述

卷积函数

什么是卷积

在这里插入图片描述

离散卷积与多维卷积

在这里插入图片描述

生活中的卷积

在这里插入图片描述

卷积神经网络

全连接神经网络的局限

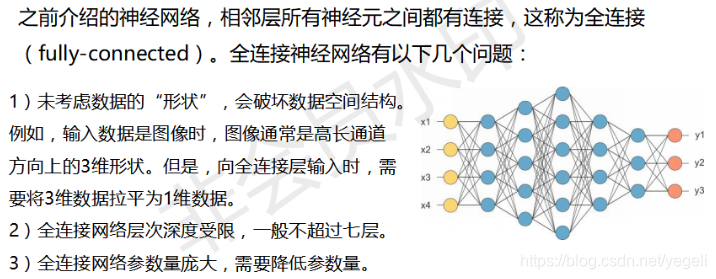
在这里插入图片描述

什么是卷积神经网络

在这里插入图片描述

卷积神经网络的用途

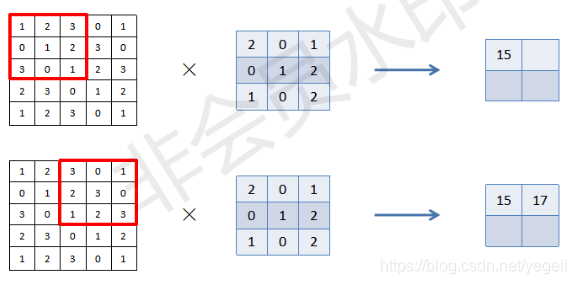
在这里插入图片描述

卷积运算

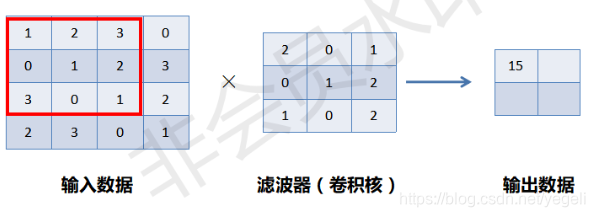
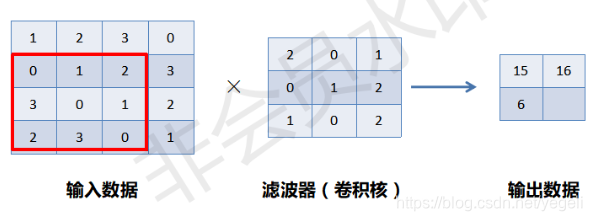
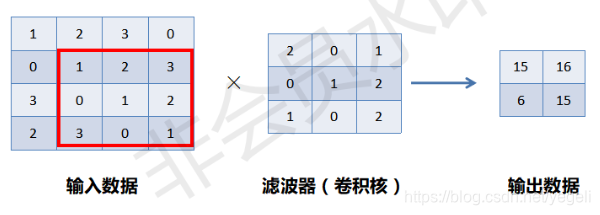
单通道、二维卷积运算示例

相同位置相乘再相加
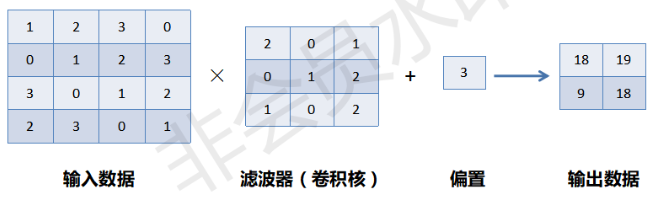
在这里插入图片描述

单通道、二维带偏置的卷积运算示例

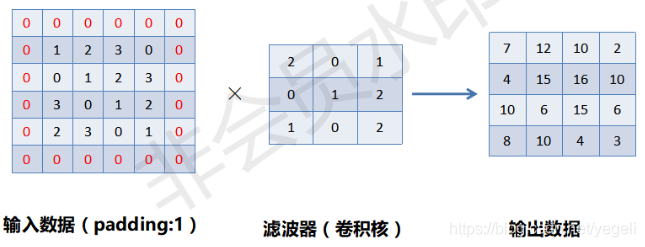
在这里插入图片描述

带填充（padding）的单通道、二维卷积运算示例

在这里插入图片描述

步幅（stride）为2的卷积算示例

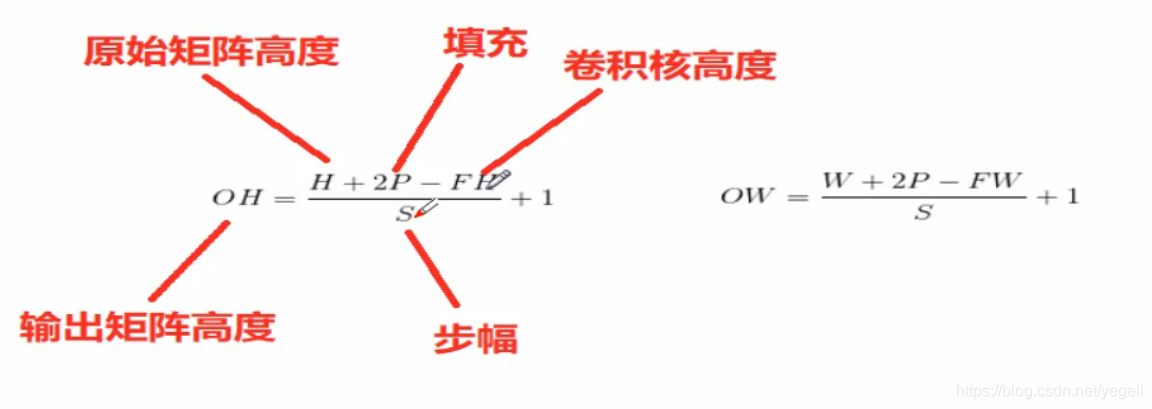
在这里插入图片描述

卷积运算输出矩阵大小计算公式

在这里插入图片描述

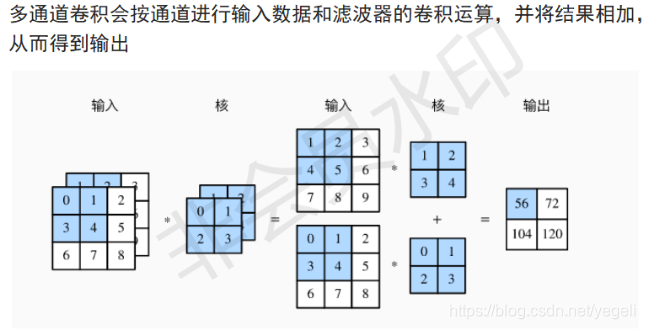
多通道卷积

在这里插入图片描述
#####

卷积运算的效果

在这里插入图片描述

案例2：图像卷积运算

在这里插入图片描述

卷积神经网络结构

总体结构

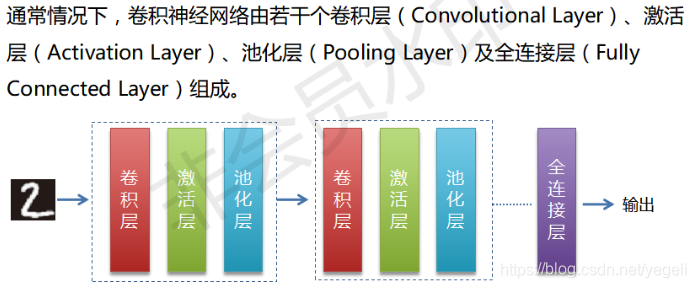
在这里插入图片描述

卷积层

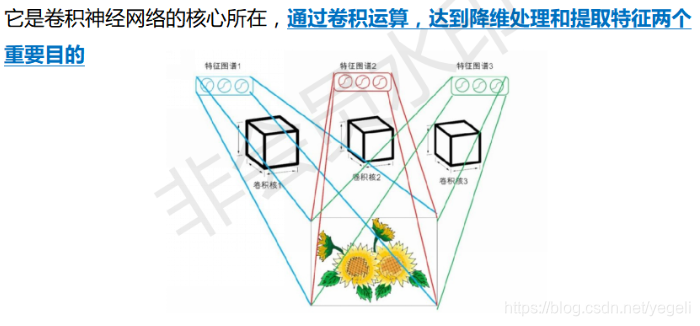
在这里插入图片描述

激活层

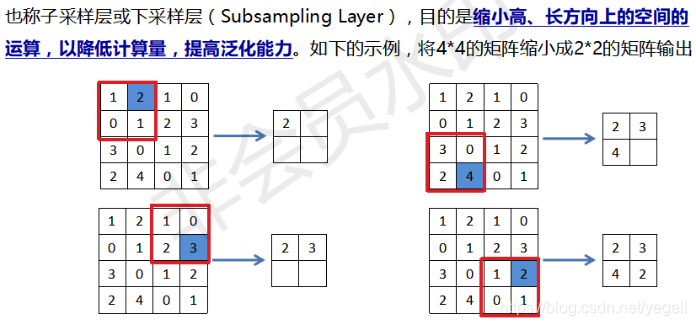
在这里插入图片描述

池化层

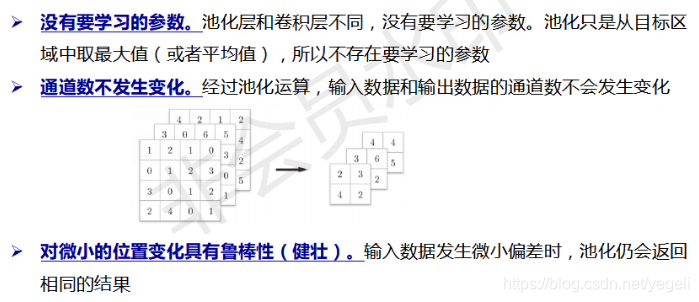
在这里插入图片描述

池化层计算

在这里插入图片描述

池化层的特征

在这里插入图片描述

全连接层

在这里插入图片描述

典型CNN介绍

LeNet：主要参数

在这里插入图片描述

AlexNet：特点

在这里插入图片描述

AlexNet：主要参数

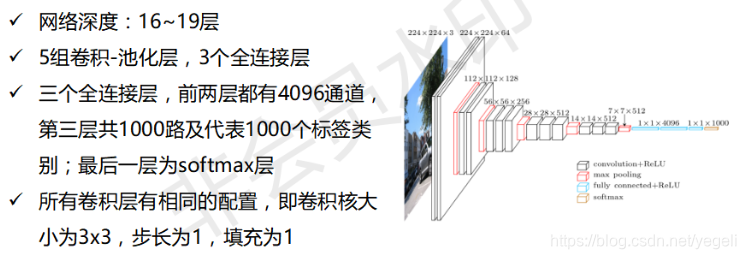
在这里插入图片描述

VGG：概要介绍

在这里插入图片描述

VGG：主要参数

在这里插入图片描述

小结

在这里插入图片描述

总结

在这里插入图片描述

posted @ 2020-07-13 17:20 野哥李阅读(47) 评论(0) 收藏举报来源

刷新页面返回顶部