常用编程技巧(C++篇)
基础知识
long long和int的大小区别
| 数据类型 | 字节数(通常) | 最小值(有符号) | 最大值(有符号) | 最大值(无符号) |
|---|---|---|---|---|
int |
4 字节 | -2,147,483,648 (-2^31) |
2,147,483,647 (2^31 - 1) |
4,294,967,295 (2^32 - 1) |
long |
8 字节 (64位) / 4 字节 (32位) | 视平台而定(常为 -2^63 或 -2^31) |
2^63 - 1 或 2^31 - 1 |
2^64 - 1 或 2^32 - 1 |
long long |
8 字节 | -9,223,372,036,854,775,808 (-2^63) |
9,223,372,036,854,775,807 (2^63 - 1) |
18,446,744,073,709,551,615 (2^64 - 1) |
float和double的区别
| 类型 | 存储大小 | 有效数字(十进制) | 典型范围(绝对值) |
|---|---|---|---|
float |
4字节 | 6~7位 | 约 1.2e-38 到 3.4e38 |
double |
8字节 | 15~16位 | 约 2.3e-308 到 1.7e308 |
通分公式
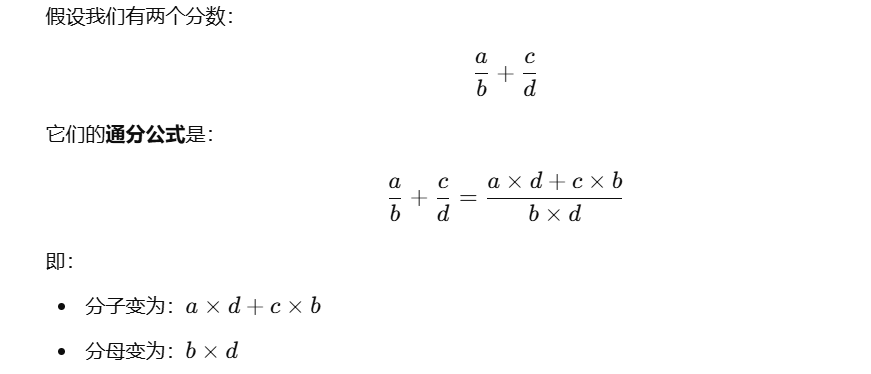
最大公约数
// 计算最大公约数(GCD)
int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
这个函数使用的是欧几里得算法(也叫辗转相除法),它的基本原理是:
两个整数 a 和 b(假设 a ≥ b)的最大公约数等于 b 和 a % b 的最大公约数,即:
gcd(a, b) = gcd(b, a % b)
如何把一个分数拆分开整数+分数

阶乘
阶乘(factorial)是基斯顿·卡曼(Christian Kramp,1760~1826)于1808年发明的运算符号 [1].正整数的阶乘定义为所有小于及等于该数的正整数的积,记为n!,例如5的阶乘表示为5!,其值为120:5!=1×2×3×4×5=120.
阶乘运算满足递推公式n!=n·(n-1)!
特别地,定义1!=1,0!=1
素数
定义:质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数
2、3、5、7、11、13、17、19......
英文名:Prime
//基础版
bool isPrime(int n){
if(n<2) return false;
for(int i=2;i<n;i++){
if(n % i == 0) return false;
}
return true;
}
//优化版
bool isPrime(int n){
if(n<2) return false; // 排除小于2的情况
if(n==2) return true; // 2是唯一的偶素数
if(n%2==0) return false;
for(int i=3;i<=sqrt(n);i+=2){ //只检查奇数,并且只检查到最大因子对√n附近,缩小范围,节省时间
if(n%i==0)return false; //发现因子,说明不是素数
}
return true;
}
排列组合
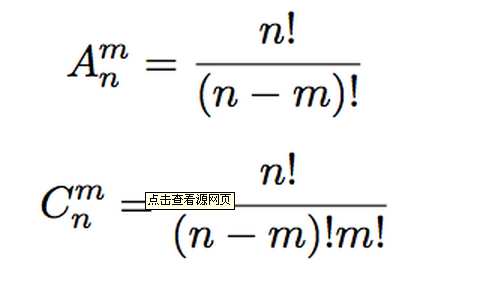
排序就是从n个数里面选出r个数,但是有顺序
组合就是从n个数里面选出r个数,但是没有顺序
#include <bits/stdc++.h>
using namespace std;
/*
排列 P(5, 3) = 60
组合 C(5, 3) = 10
*/
// 计算阶乘
long long factorial(int n){
long long result = 1;
for(int i=1;i<=n;i++){
result *= i;
}
return result;
}
// 计算排列数P(n,r)
long long permutation(int n,int r){
return factorial(n)/factorial(n-r);
}
// 计算组合数C(n,r)
long long combination(int n,int r){
return factorial(n)/(factorial(n-r)*factorial(r));
}
int main(){
int n, r;
cout << "请输入n和r的值(n >= r):";
cin >> n >> r;
cout << "排列 P(" << n << ", " << r << ") = " << permutation(n, r) << endl;
cout << "组合 C(" << n << ", " << r << ") = " << combination(n, r) << endl;
return 0;
}
判断是否是闰年
2月的天数取决为年份:
普通年:2月有 28天。
闰年:2月有 29天。
闰年的判断规则是:
- 能被400整除的年份,例如2000
- 能被4整除且不能被100整除的年份,例如2024
子序列和子串的区别
子序列 的定义就是:从一个序列中选择若干个元素,且它们的相对顺序不能改变。
子序列的元素在原数组中可以隔开!只要顺序保持不变就行。
⚠️ 子序列 vs 子串(substring)的区别:
| 特性 | 子序列 (Subsequence) | 子串 / 连续子序列 (Substring) |
|---|---|---|
| 是否必须连续 | ❌ 不需要连续 | ✅ 必须连续 |
| 顺序是否重要 | ✅ 必须保持顺序 | ✅ 必须保持顺序 |
| 可跳过元素 | ✅ 可以 | ❌ 不可以 |
秦九韶算法
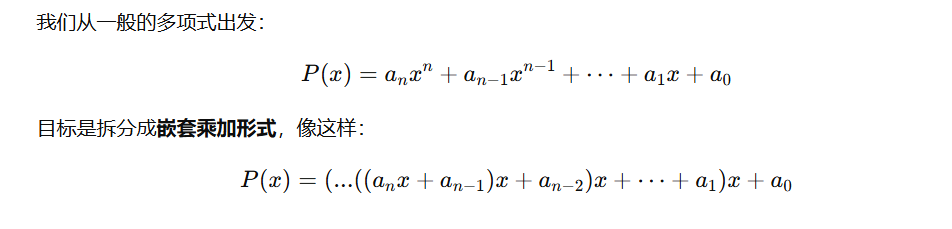


简单地说就是从最左侧开始,每次都提取一个x出来加上后面的一个常数项,然后乘上一个x
#include <iostream>
#include <vector>
using namespace std;
// Horner 方法(降幂系数版本)
double horner_descending(const vector<double>& coefficients, double x) {
double result = coefficients[0]; // 从最高次项开始
for (int i = 1; i < coefficients.size(); ++i) {
result = result * x + coefficients[i];
}
return result;
}
int main() {
// 多项式:P(x) = 2x^3 - 6x^2 + 2x - 1
vector<double> coefficients = {2, -6, 2, -1}; // 降幂排序 a_3 到 a_0
double x = 3;
double value = horner_descending(coefficients, x);
cout << "P(" << x << ") = " << value << endl;
return 0;
}
常用技巧(C++篇)
万能头文件
- 定义:
<bits/stdc++.h>是GCC编译器特有的头文件,非C++标准库的一部分。它通过包含其他所有标准头文件(如<iostream>、<vector>、<algorithm>等),让开发者无需手动逐个添加。 - 用途:主要用于编程竞赛或测试场景,节省编写头文件的时间。
#include <bits/stdc++.h>
using namespace std;
int main() {
vector<int> nums = {3, 1, 4, 1, 5};
sort(nums.begin(), nums.end()); // 直接使用算法库的排序
cout << "排序后: ";
for (int num : nums) {
cout << num << " ";
}
return 0;
}
Dev-C++软件开启C++11
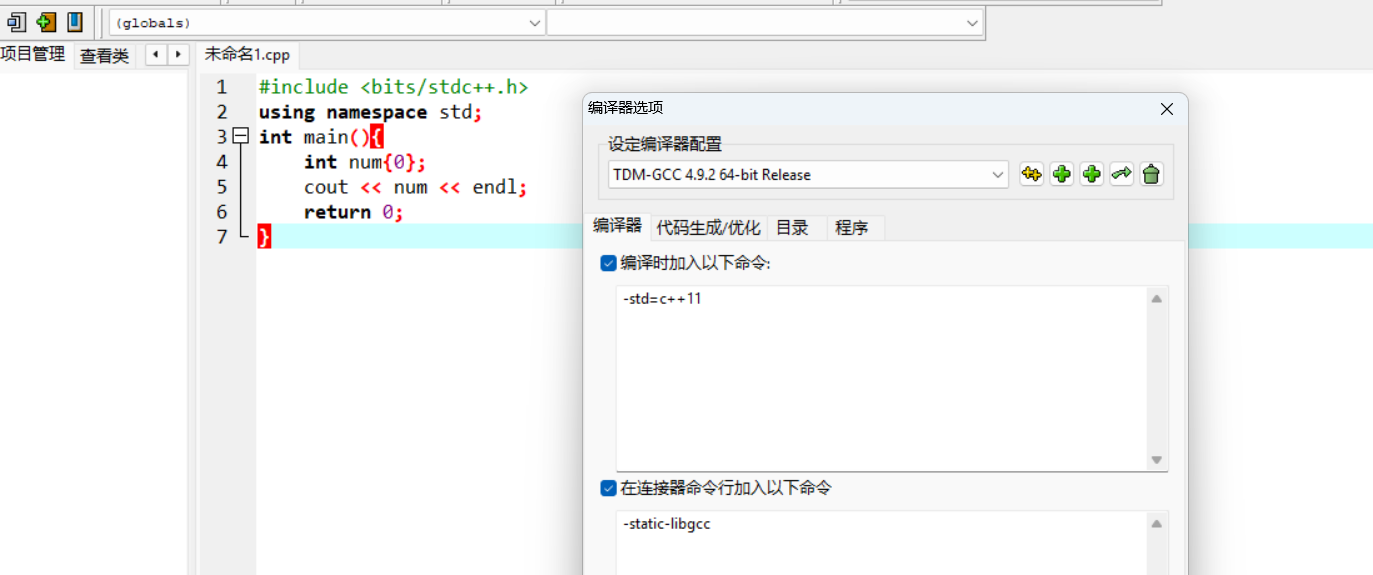
C++ 做题模板
#include <bits/stdc++.h>
using namespace std;
#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) //作用是加快C++输入输出的速度
int main() {
ios;
return 0;
}
注意:如果用了这个宏,就不要再用 scanf/printf,全部用 cin/cout 就好。以及使用\n代替endl
二维vector的定义
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<vector<int>> vec = {{1,2,3},{1,4,5}}; //注意是如何定义的
for(int i=0;i<vec.size();i++){
for(int j=0;j<vec[i].size();j++){
cout << vec[i][j] << " ";
}
}
}
vector 求和
使用 accumulate() 来对 vector 求和:
#include <numeric>
accumulate(first, last, init); // 起始迭代器、结束迭代器、初始值
示例:
#include <iostream>
#include <vector>
#include <numeric>
using namespace std;
int main() {
vector<int> vec = {1, 2, 3, 4, 5};
int sum = accumulate(vec.begin(), vec.end(), 0);
cout << "sum: " << sum << endl;
return 0;
}
位运算算2的n次方
#include <bits/stdc++.h>
using namespace std;
int main(){
int N;
cin >> N;
long long result = 1LL << N; //1LL << N 表示将数字 1 左移 N 位,等价于计算 2^N
cout << "2^" << N << " = " << result << endl;
return 0;
}
输入一个 n,然后输入 n 次
int x;
while (n--) {
cin >> x;
vec.push_back(x);
}
左对齐和右对齐以及设置字段宽度
%4d和%04d的区别:
%04d表示宽度为 4,且用 0 进行填充(如不足 4 位)。
%4d表示宽度为 4,默认使用空格填充(右对齐)。
%-4d 表示左对齐(在右侧填充空格)。
下面是C++的写法
cout << left << setw(5) << 42 << right << setw(5) << 99;
c++引用结合for循环使用
可以节省空间的消耗
for (int &num : vec) cin >> num;
&num 是对 vec 里元素的引用,即 num 直接指向 vec 的元素本身,所以修改 num 就等于修改 vec 里的值。
读取一整行字符串
string line;
getline(cin, line);
cout << line;
⚠️ 注意:若
cin和getline混用,需加cin.ignore()清空缓冲区。
min,max函数的使用
作用:
- 两个变量的比较
- 找出数组中最大的值(C++11支持)
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int a = 10, b = 20;
cout << "最大值:" << max(a,b) << endl;
cout << "最大值:" << max({3,1,4,1,5}) << endl;
return 0;
}
注意点:
- 注意变量名别冲突
- 变量类型需一致才可以比较
字符和 ASCII 码互转
字符转 ASCII
char ch = 'A';
int ascii = ch;
cout << ascii; // 输出 65
ASCII 转字符
int code = 97;
char ch = code;
cout << ch; // 输出 'a'
保留有效小数位
默认四舍五入
#include <iomanip>
cout << fixed << setprecision(2) << num;
不四舍五入(截断法)
double factor = pow(10, precision);
double truncated = static_cast<int>(num * factor) / factor;
cout << fixed << setprecision(precision) << truncated;
整除与非整除
int a = 7, b = 2;
cout << a / b; // 3
float x = 7, y = 2;
cout << x / y; // 3.5
结构体排序
struct Person {
string name;
int age;
};
vector<Person> people = {
{"Alice", 25},
{"Bob", 20},
{"Charlie", 30}
};
sort(people.begin(), people.end(), [](const Person &a, const Person &b) { //捕获列表,参数列表,函数体
return a.age < b.age;
});
判断素数函数
bool is_Prime(int n) {
if (n <= 1) return false;
if (n == 2) return true;
if (n % 2 == 0) return false;
for (int i = 3; i <= sqrt(n); i += 2) {
if (n % i == 0) return false;
}
return true;
}
示例使用:
int nums[] = {1,2,3,4,5,6,7,8,9,10,11,12,13};
for (auto num : nums) {
if (is_Prime(num)) cout << "Yes:" << num << " ";
else cout << "No:" << num << " ";
}
cmath库常用函数
#include <iostream>
#include <cmath>
using namespace std;
int main() {
cout << "返回整数x的绝对值:" << abs(-3) << endl;
cout << "返回x的y次方:" << pow(2.0,3.0) << endl;
cout << "返回x的平方根:" << sqrt(4) << endl;
cout << "返回x的四舍五入:" << round(4.33) << endl;
cout << "向下取整:" << floor(5.93) << endl;
cout << "向上取整:" << ceil(5.03) << endl;
}
编程误区
sort函数的使用
sort(rate[0],rate[N]); //错误的
std::sort(rate, rate + N); //正确的
min和max命名变量冲突
double min, max;
min 和 max 是 C++ 标准库 <algorithm> 中的函数名,定义同名变量会与这些函数冲突,造成难以预料的问题。建议换成其他名字,比如 minVal, maxVal,或者如果不需要可以去掉。
在while循环里面修改for循环的自增变量
错误的
for (int i = 11; i < 12; i++)
{
while (i > 0)
{
cout << "i: " << i << endl;
i = i / 10;
cout << "i: " << i << endl;
cout << "执行完了!" << endl;
}
}
虽然 for (int i = 11; i < 12; i++) 表面看起来会执行一次,但因为你在 while 循环里 修改了 i 的值,导致 for 循环控制变量的逻辑被破坏。
正确的
for (int i = 11; i < 12; i++)
{
int temp = i; // 用 temp 来处理除法
while (temp > 0)
{
cout << "i: " << temp << endl;
temp = temp / 10;
cout << "i: " << temp << endl;
cout << "执行完了!" << endl;
}
}
正向思维转逆向思维
正向思维:
for (int i = 10; i < 11; i++)
{
int odd_index = 1;
int flag = 0;
int current_num = i;
while (current_num > 0)
{
int last_number = current_num % 10;
cout << "last_number:" << last_number << endl;
// 奇数位判断
if ((odd_index == 1) && (last_number % 2 != 0))
{
cout << "奇数位" << endl;
odd_index = 0;
flag = 1;
}
// 偶数位判断
else if ((odd_index == 0) && (last_number % 2 == 0))
{
cout << "偶数位" << endl;
odd_index = 1;
flag = 1;
}
else
{
flag = 0;
}
current_num = current_num / 10;
}
if (flag == 1)
{
cout << i << " ";
}
}
有时候,使用逆向思维会有奇效。
逆向思维:
#include <iostream>
using namespace std;
int good_number(int n)
{
// int count=0;
/* 判断偶数位或者奇数位 */
/* 数字转字符串,怎么指向最后一位 */
/* 99 19 */
// 2025年4月8日19:18:18
int count=0;
for (int i = 1; i < n; i++)
{
int odd_index = 1;
int flag = 0;
int current_num = i;
while (current_num > 0)
{
int last_number = current_num % 10;
// cout << "last_number:" << last_number << endl;
// 奇数位判断,如果奇数位是偶数直接退出
if ((odd_index == 1) && (last_number % 2 == 0))
{
// cout << "奇数位不满足" << endl;
flag = 0;
break;
}
// 偶数位判断,如果偶数位是奇数直接退出
else if ((odd_index == 0) && (last_number % 2 != 0))
{
// cout << "偶数位不满足" << endl;
flag = 0;
break;
}
else
{
flag = 1;
}
current_num = current_num / 10;
odd_index = !odd_index; //取反odd_index;
}
if (flag == 1)
{
// cout << i << " ";
count++;
}
}
return count;
}
int main()
{
cout<<good_number(2024)<<endl;
return 0;
// cout << 1/10 << endl;
}
数据类型不同参与运算的精度丢失
错误的:
#include <bits/stdc++.h>
#include <cmath>
using namespace std;
int main(){
double num,n;
cin >> n >> num;
cout << round(num*pow(2,n)) << endl; //pow(2, n) 的返回值类型是 double,而用 int 来接收或参与计算时,可能出现精度问题或逻辑上的误差。
return 0;
}
正确的:
num和n采用double的类型
#include <bits/stdc++.h>
#include <cmath>
using namespace std;
int main(){
double num,n;
cin >> n >> num;
cout << round(num*pow(2,n)) << endl; //pow(2, n) 的返回值类型是 double,而用 int 来接收或参与计算时,可能出现精度问题或逻辑上的误差。
return 0;
}
进阶的:
#include <bits/stdc++.h>
#include <cmath>
using namespace std;
int main(){
int n;
long double num;
cin >> n >> num;
long double factor = powl(2.0L,n);
long double res = num * factor;
cout << llroundl(res) << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号