基于模拟退火算法的多个城市变速环游算法设计及其可视化——python实现

目录

• 说明
• 代码

说明

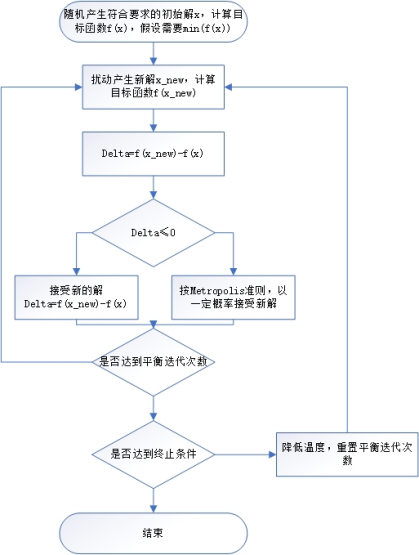
1.4实验结果例子
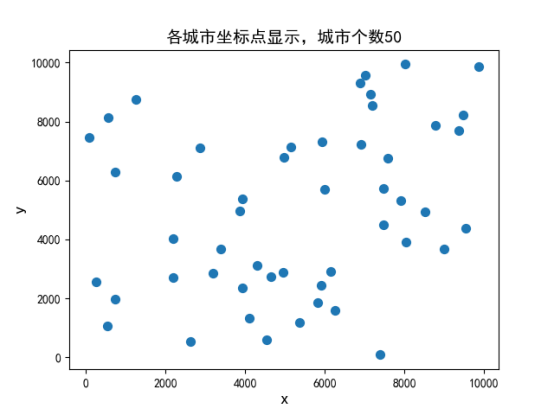
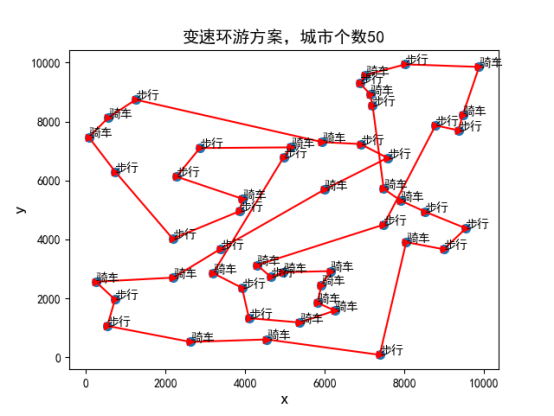
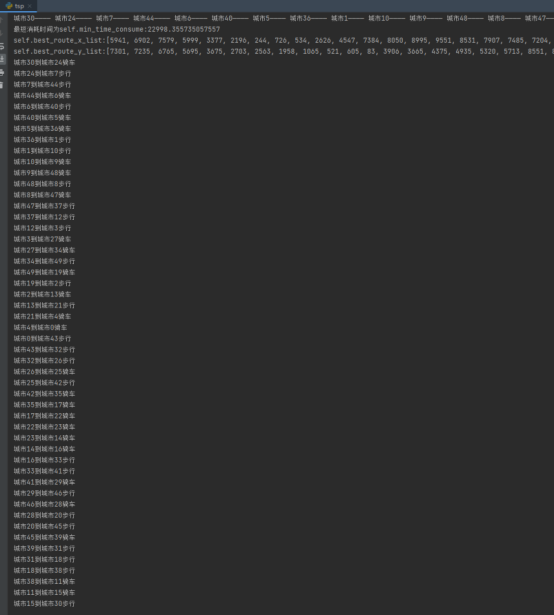
城市坐标点为随机数随机产生，结果如图2、3、4所示。



参考文献：
[1] Steinbrunn M , Moerkotte G , Kemper A . Heuristic and randomized optimization for the join ordering problem[J]. Vldb Journal, 1997, 6(3):191-208.

代码

"""
假设有N个城市编号为1~N，分布在二维平面上，其坐标分别为(Xi, Yi)。城市间的距离按照欧式距离计算。现任选一个城市出发，不重复、不遗漏地访问
其他所有城市，最终返回源点，形成一条封闭路径，与旅行商问题类似。现假设在任两个城市间均按直线行进，可以选择步行或骑车，后者的速度是前者的k倍，
在本题中令k=2。若封闭路径中记为p0-p1-p2-...pN，其中pi是第i步访问的城市编号，初始位置p0和结束位置pN相同。相邻两个城市（pi到pi+1）的访问
仅能选择步行或骑车之一进行，在途中不能变更交通方式。在到达目标城市之后不作停留，继续向下一个城市出发，但出发时允许变更交通方式。此外，城市间
骑车的总次数不能超过N的一定比例，本题为w=50%，即上述路径中的N段旅程，仅能有不超过wN段骑车。

根据上述条件，设计算法实现用时最短的环游路线，并给出路线上相邻城市间采用哪种交通方式。如难以找到最短路线，可以寻找次优解。
要求：给出问题的数学规范描述和解题思路，给出算法的规范描述，完成算法实现与性能分析（理论分析或实测分析均可）。
"""
import random
import sys
import copy
import math
import matplotlib.pyplot as plt

# 使能够正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
random.seed(10)

city_number = 50  # 城市个数
walking_speed = 2
"""定义参数"""
parameter_dict = {
    "city_number": city_number,
    "city_x_list": random.sample(range(1, 10000), city_number),
    "city_y_list": random.sample(range(1, 10000), city_number),
    "walking_speed": walking_speed,
    "cycling_speed": 2 * walking_speed,
    "cycling_number_threshold": int(city_number / 2),
    "satisfying_value": sys.maxsize,  # 满意值
    "break_T": 1  # 模拟退火算法跳出温度
}

print(f"parameter_dict:{parameter_dict}")
"""end"""


class DrawPoint(object):
    """画点的类"""

    def __init__(self):
        self.fontsize = 14
        self.scatter_s = 50
        self.connect_point_color = 'r'
        self.plot_marker = '>'
        self.plt_obj = plt

    def draw_points(self, point_x_axis_list: list, point_y_axis_list: list, xlabel: str, ylabel: str, title: str):
        """把点显示出来"""
        self.plt_obj.scatter(point_x_axis_list, point_y_axis_list, s=self.scatter_s)
        # # 设置图表标题并给坐标轴加上标签
        self.plt_obj.title(title, fontsize=self.fontsize)
        self.plt_obj.xlabel(xlabel, fontsize=self.fontsize)
        self.plt_obj.ylabel(ylabel, fontsize=self.fontsize)

    def connect_points(self, point_x_axis_list: list, point_y_axis_list: list):
        """按顺序连接各点"""
        self.plt_obj.plot(point_x_axis_list, point_y_axis_list, color=self.connect_point_color, marker=self.plot_marker)

    def show_text(self, point_x_axis_list, point_y_axis_list, best_route, best_route_detail):
        """把方案方式显示到点上"""
        for i in range(len(best_route)):
            plt.text(point_x_axis_list[i], point_y_axis_list[i], best_route_detail[f"{best_route[i]}"])

    def plt_show(self):
        self.plt_obj.show()


draw_obj = DrawPoint()
draw_obj.draw_points(point_x_axis_list=parameter_dict["city_x_list"], point_y_axis_list=parameter_dict["city_y_list"],
                     xlabel="x", ylabel="y",
                     title=f"各城市坐标点显示，城市个数{city_number}")
# draw_obj.connect_points(point_x_axis_list=parameter_dict["city_x_list"],
#                         point_y_axis_list=parameter_dict["city_y_list"])
draw_obj.plt_show()


class SimulatedAnnealingTSP(object):
    """模拟退火算法解tsp问题"""

    def __init__(self, parameter_dict):

        """跳出条件"""
        self.satisfying_value = parameter_dict["satisfying_value"]
        self.break_T = parameter_dict["break_T"]

        """tsp属性"""
        self.walking_speed = parameter_dict["walking_speed"]  # 步行速度
        self.cycling_speed = parameter_dict["cycling_speed"]  # 骑车速度
        self.cycling_number_threshold = parameter_dict["cycling_number_threshold"]  # 骑车总次数
        self.city_x_list = parameter_dict["city_x_list"]  # 城市x坐标
        self.city_y_list = parameter_dict["city_y_list"]  # 城市y坐标
        self.best_route_x_list = None  # 找到最优方案时重新排序下城市坐标
        self.best_route_y_list = None
        self.city_number = parameter_dict["city_number"]
        self.distance_matrix = [[0 for col in range(self.city_number)] for raw in
                                range(self.city_number)]  # 都初始化为0，用二维列表表示吧
        self.cur_route = None  # 用来存当前环游方案
        self.best_route = None  # 用来存储最好的环游方案
        self.best_route_detail = {}  # 骑车和步行的细节
        self.cur_total_distance = 0  # 当前方案总距离
        self.best_total_distance = 0  # 最好的方案总距离
        self.cur_time_consume = sys.maxsize  # 当前方案耗时
        self.min_time_consume = sys.maxsize  # 最好的方案耗时

        """模拟退火属性"""
        self.T = 200.0  # 温度
        self.af = 0.95  # af退火率
        self.balance = 500  # 平衡次数

    def get_distance_matrix(self):
        """得到距离矩阵，距离用欧氏距离"""
        for i in range(self.city_number):  # 行
            for j in range(self.city_number):  # 列  先计算第一行中，城市1和城市1的距离，城市1和城市2的距离，城市3和城市3的距离......
                self.distance_matrix[i][j] = pow(
                    pow(self.city_x_list[i] - self.city_x_list[j], 2) + pow(self.city_y_list[i] - self.city_y_list[j],
                                                                            2), 0.5)
                if self.distance_matrix[i][j] == 0:  # 当为0时是重叠或者起点，这个时候没有意义，设置为sys.maxsize
                    self.distance_matrix[i][j] = sys.maxsize

    def calculate_distance(self, route):
        """根据传入的方案，计算当前方案的总距离"""
        temp_total_distance = 0.0  # 每次计算当前总距离都要清0
        for i in range(self.city_number - 1):
            temp_total_distance += self.distance_matrix[route[i]][route[i + 1]]  # 路径方案中城市1和城市2的距离+城市2和城市3+......
        temp_total_distance += self.distance_matrix[route[self.city_number - 1]][route[0]]  # 再+终点城市和起点城市的距离，就齐了

        return temp_total_distance

    # 得到新解
    def get_new_route(self, route):
        """获得新的方案"""
        new_route = copy.copy(route)  # 复制一个一模一样的列表

        if random.random() < 0.5:  # 一半的概率两两交换，一半的概率三变换
            """两两交换"""
            # 随机选2个城市，都是整数
            two_cities = random.sample(range(0, self.city_number), 2)
            city1 = two_cities[0]
            city2 = two_cities[1]
            # 交换
            temp_value = new_route[city1]
            new_route[city1] = new_route[city2]
            new_route[city2] = temp_value
        else:
            """三三交换 城市1——>城市3， 城市2——>城市1， 城市3——>城市2"""
            # 随机选3个城市
            three_cities = random.sample(range(0, self.city_number), 3)
            three_cities.sort()
            city1 = three_cities[0]
            city2 = three_cities[1]
            city3 = three_cities[2]

            # 交换
            city1_temp = new_route[city1]
            new_route[city1] = new_route[city2]
            new_route[city2] = new_route[city3]
            new_route[city3] = city1_temp

        return new_route

    def calculate_time_consume(self, route):
        """根据传入的方案，计算方案的总时间损耗, 路径最长的骑车，剩下走路"""
        walking_distance = 0
        cycling_distance = 0
        each_two_cities_distance = []  # 每2个城市之前的距离
        # 各个城市之前的距离
        for i in range(self.city_number - 1):
            each_two_cities_distance.append(self.distance_matrix[route[i]][route[i + 1]])
        each_two_cities_distance.append(self.distance_matrix[route[self.city_number - 1]][route[0]])
        # 计算步行和骑车总距离
        each_two_cities_distance.sort(reverse=True)  # 从大到小排序
        for i in range(len(each_two_cities_distance)):
            if i + 1 <= self.cycling_number_threshold:  # 距离长的就骑车
                cycling_distance += each_two_cities_distance[i]
            else:
                walking_distance += each_two_cities_distance[i]
        # 计算步行和骑车总时间
        walking_time = walking_distance / self.walking_speed
        cycling_time = cycling_distance / self.cycling_speed

        # 消耗的总时间
        time_consume = walking_time + cycling_time

        return time_consume

    def get_best_route_detail(self, route):
        """根据传入的方案，获得骑车和步行的细节"""
        self.best_route_detail = {}

        each_two_cities_distance = []
        each_two_cities_distance_and_indexs = {}  # 每2个城市之前的距离和索引
        # 各个城市之前的距离
        for i in range(self.city_number - 1):
            each_two_cities_distance.append(int(self.distance_matrix[route[i]][route[i + 1]]))
            each_two_cities_distance_and_indexs[f"{int(self.distance_matrix[route[i]][route[i + 1]])}"] = i
        each_two_cities_distance.append(int(self.distance_matrix[route[self.city_number - 1]][route[0]]))
        each_two_cities_distance_and_indexs[
            f"{int(self.distance_matrix[route[self.city_number - 1]][route[0]])}"] = self.city_number - 1
        # 计算步行和骑车总距离
        each_two_cities_distance.sort(reverse=True)  # 从大到小排序
        for i in range(len(each_two_cities_distance)):
            # 获取此时距离的route索引
            route_index = each_two_cities_distance_and_indexs[f"{each_two_cities_distance[i]}"]
            if i + 1 <= self.cycling_number_threshold:  # 距离长的就骑车
                self.best_route_detail[f"{route_index}"] = "骑车"
            else:
                self.best_route_detail[f"{route_index}"] = "步行"
        # print(f"self.best_route_detail:{self.best_route_detail}")

        for i in range(len(self.best_route)):
            how_to_arrice = self.best_route_detail[f"{self.best_route[i]}"]
            if i + 1 < self.city_number:
                print(f"城市{self.best_route[i]}到城市{self.best_route[i + 1]}{how_to_arrice}   ")
            else:
                print(f"城市{self.best_route[i]}到城市{self.best_route[0]}{how_to_arrice}   ")

    def run(self):
        # 根据欧式距离得到距离矩阵
        self.get_distance_matrix()
        # 初始化方案
        self.cur_route = random.sample(range(0, city_number), city_number)  # 随机选择列表序列中元素完成初始化路径，用索引来表示城市
        # 计算初始化方案的距离和时间
        self.cur_total_distance = self.calculate_distance(self.cur_route)
        self.cur_time_consume = self.calculate_time_consume(self.cur_route)
        # 初始方案和最优值初始化
        self.best_route = self.cur_route
        self.best_total_distance = self.cur_total_distance
        self.min_time_consume = self.cur_time_consume

        while True:
            """迭代次数"""
            for j in range(self.balance):
                new_route = self.get_new_route(self.cur_route)  # 获取新方案
                new_time_consume = self.calculate_time_consume(new_route)  # 计算新方案的总耗时

                if new_time_consume <= self.cur_time_consume:  # 新方案耗时更小，也就是更好
                    self.cur_route = new_route  # 接受新解
                    self.cur_time_consume = new_time_consume
                    if new_time_consume < self.min_time_consume:  # 如果新方案比最好的方案还要好，新解为最优解
                        self.best_route = new_route
                        self.min_time_consume = new_time_consume
                elif new_time_consume > self.cur_time_consume:  # 新方案耗时更大，也就是比当前方案要差了，那就以一点概率接受这个更差的解
                    p = math.exp(-(new_time_consume - self.cur_time_consume) / self.T)
                    if random.uniform(0, 1) < p:
                        self.cur_route = new_route
                        self.cur_time_consume = new_time_consume

            self.T = self.T * self.af  # 温度下降

            """跳出条件, 达到满意的解或者温度直接跳出"""
            if self.best_total_distance > self.satisfying_value or self.T < self.break_T:
                break

        print(f"最佳方案self.best_route为:{self.best_route}")
        for i in self.best_route:
            print(f"城市{i}————", end=" ")
        print(f"\n最短消耗时间为self.min_time_consume:{self.min_time_consume}")

        # 根据最新方案索引重新排序x和y列表
        self.best_route_x_list = [self.city_x_list[i] for i in self.best_route]
        self.best_route_x_list.append(self.best_route_x_list[0])  # 要把初始点再加上去，就能回到初始点了
        self.best_route_y_list = [self.city_y_list[i] for i in self.best_route]
        self.best_route_y_list.append(self.best_route_y_list[0])  # 要把初始点再加上去，就能回到初始点了
        print(f"self.best_route_x_list:{self.best_route_x_list}")
        print(f"self.best_route_y_list:{self.best_route_y_list}")

        # 获得骑车和步行细节信息
        self.get_best_route_detail(self.best_route)


SimulatedAnnealingTSP_obj = SimulatedAnnealingTSP(parameter_dict=parameter_dict)
SimulatedAnnealingTSP_obj.run()
draw_obj_tsp = DrawPoint()
draw_obj_tsp.draw_points(point_x_axis_list=parameter_dict["city_x_list"],
                         point_y_axis_list=parameter_dict["city_y_list"],
                         xlabel="x", ylabel="y",
                         title=f"变速环游方案，城市个数{city_number}")
draw_obj_tsp.connect_points(point_x_axis_list=SimulatedAnnealingTSP_obj.best_route_x_list,
                            point_y_axis_list=SimulatedAnnealingTSP_obj.best_route_y_list)
draw_obj_tsp.show_text(point_x_axis_list=SimulatedAnnealingTSP_obj.best_route_x_list,
                       point_y_axis_list=SimulatedAnnealingTSP_obj.best_route_y_list,
                       best_route=SimulatedAnnealingTSP_obj.best_route,
                       best_route_detail=SimulatedAnnealingTSP_obj.best_route_detail)
draw_obj_tsp.plt_show()