python实现蒙特卡洛算法和拟蒙特卡洛方法(Halton和Sobol序列生成)求单位圆面积
说明
一、蒙特卡洛求单位圆面积是一种模拟方法,通过随机数的落点情况,求可以求出圆的面积,基本步骤为:
(1)设圆的半径为r,x和y都在(-r,r)区间产生随机数点。
(2)计算在半径为r的圆内的点的个数。
(3)通过统计圆内的点的个数,根据以下原理,可以估计出Pi,则可得出单位圆面积。
二、实验设置:蒙特卡洛算法以及拟蒙特卡洛算法的实验误差分析设置一样。在分析采样数量与误差之间的关系时,设置半径r固定为10,采样数量分别以步长50从50-10000得到共200次结果;在分析半径与误差之前的关系,固定采样数量为1000,半径分别以步长5从1-1000获得共200次结果。
三、实验结论与分析:
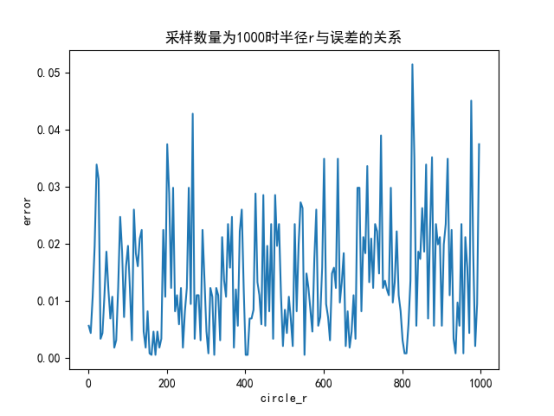
(1)蒙特卡洛算法求单位圆面积时,采样数量和圆的半径都会对误差有影响。采样数量越大,误差越小。圆的半径有影响但无规律,只是震荡。
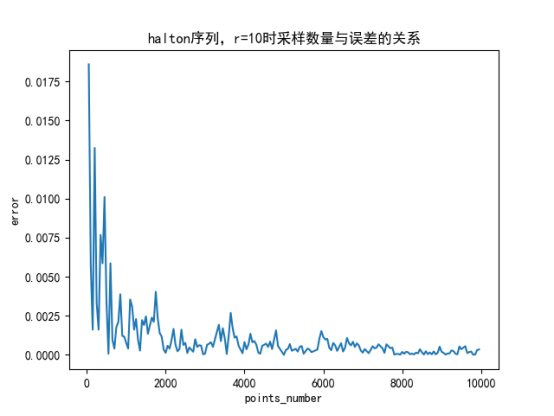
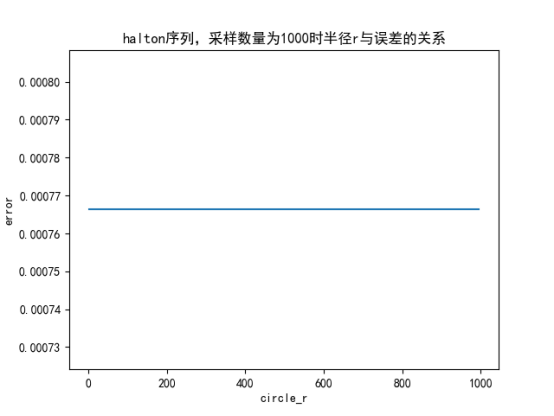
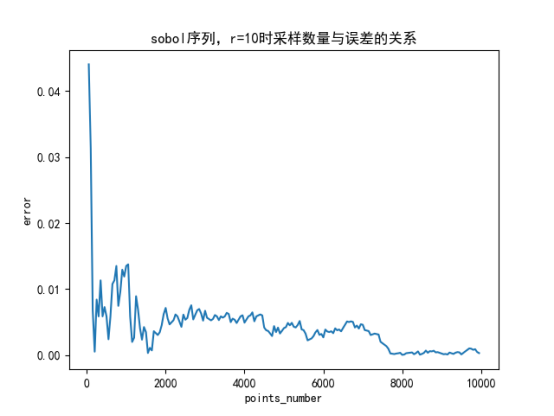
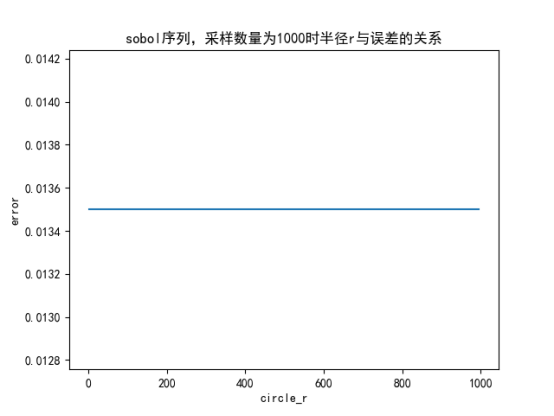
(2)拟蒙特卡洛算法求单位圆面积时,无论是Halton序列还是Sobol序列生成的拟随机数求的单位圆面积,都是:采样数量越大,误差越小;且圆的半径变化对误差无影响。
(3)拟蒙特卡洛算法和蒙特卡洛算法相比不同点在于:随着采样数量增大时,拟蒙特卡洛算法比蒙特卡洛算法更稳定,误差震荡更小,且误差不随半径的变化而变化。
造成拟蒙特卡洛算法和蒙特卡洛算法的主要原因是拟蒙特卡洛算法产生的拟随机数是均匀的,比蒙特卡洛算法更稳定,如图所示:
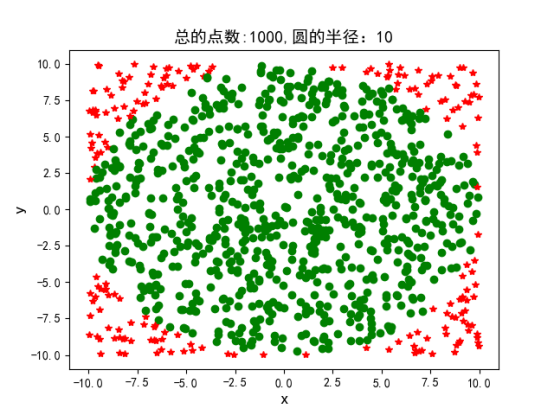
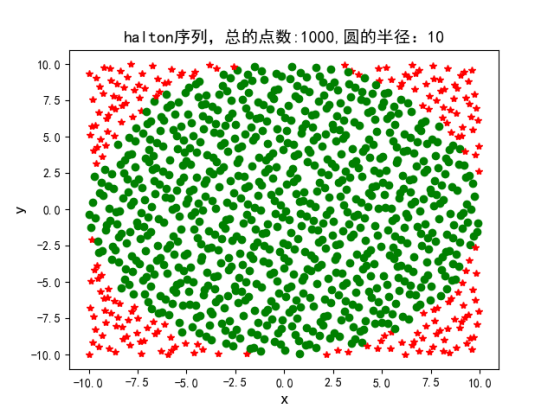
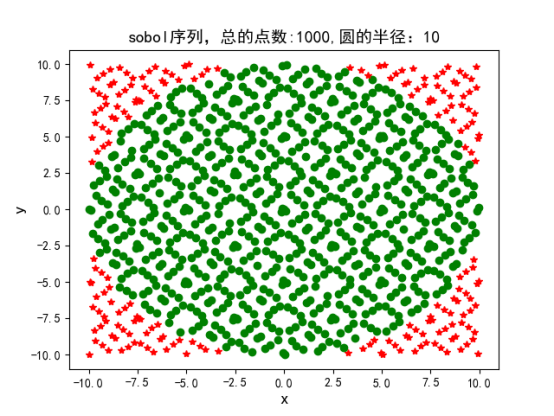
四、实验结果如下:
1、蒙特卡洛算法求单位圆面积
1.1、误差分析——采样数量与误差之间的关系 此时固定为r=10
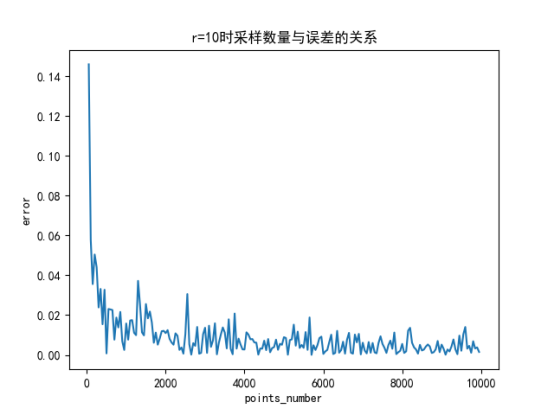
1.2、误差分析——半径与误差之前的关系 此时固定为采样数量为1000
2、拟蒙特卡洛算法求单位圆面积
2.1、Halton序列
2.2、Sobol序列
代码
"""
利用蒙特卡洛算法求单位圆面积,分析采样数量和面积误差间的关系。利用重要性采样或拟蒙特卡洛方法改进上述算法,并进行对比分析。
文档按规定的字体和行间距等进行排版(同上),文档提交PDF版本即可,通常在2页左右,文档中不排版代码。
"""
"""
注:需要打开画图请把实例化的is_plt_show=False改为True
"""
import random
import math
import matplotlib.pyplot as plt
from scipy.stats import qmc
# 使能够正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
random.seed(10)
class MonteCarlo(object):
"""蒙特卡洛算法求单位圆面积"""
def __init__(self, points_number, circle_r, is_plt_show=True):
self.circle_r = circle_r # 圆的半径
self.points_number = points_number # 总的点数
self.point_in_circle = 0 # 圆内的点
self.real_pi = math.pi # 真实的pi
self.estimated_pi = 0 # pi的估计值
self.error = 0 # 误差值
# 画图
self.plt_obj = plt
# 是否画图
self.is_plt_show = is_plt_show
# 画图格式
self.fontsize = 14
self.point_in_circle_format_string = 'go'
self.point_outside_format_string = 'r*'
if self.is_plt_show:
self.plt_obj.xlabel("x", fontsize=self.fontsize)
self.plt_obj.ylabel("y", fontsize=self.fontsize)
self.plt_obj.title(f"总的点数:{points_number},圆的半径:{self.circle_r}", fontsize=self.fontsize)
def monte_carlo(self):
for i in range(self.points_number):
x = random.uniform(-self.circle_r, self.circle_r) # 产生随机数
y = random.uniform(-self.circle_r, self.circle_r)
if math.sqrt(x ** 2 + y ** 2) <= self.circle_r: # 点在圆内
self.point_in_circle += 1
if self.is_plt_show:
self.plt_obj.plot(x, y, self.point_in_circle_format_string)
else:
if self.is_plt_show:
self.plt_obj.plot(x, y, self.point_outside_format_string)
if self.is_plt_show:
self.plt_obj.show()
self.estimated_pi = 4.0 * self.point_in_circle / self.points_number
self.error = abs(self.real_pi - self.estimated_pi) / self.real_pi
self.print_result()
def print_result(self):
print(
f"总的点数self.points_number:{self.points_number},落在圆内的点数self.point_in_circle为:{self.point_in_circle}")
print(f"估计的pi值self.estimated_pi为:{self.estimated_pi},真实的pi值self.real_pi为:{self.real_pi}")
print(f"误差为self.error:{self.error}")
class QuasiMonteCarlo(object):
"""拟蒙特卡洛算法求单位圆面积, halton和sobol序列"""
def __init__(self, points_number, circle_r, is_plt_show=True):
self.circle_r = circle_r # 圆的半径
self.points_number = points_number # 总的点数
self.point_in_circle = 0 # 圆内的点
self.real_pi = math.pi # 真实的pi
self.estimated_pi = 0 # pi的估计值
self.error = 0 # 误差值
# scipy.stats库设置
self.qmc_obj = qmc
self.l_bounds = [-self.circle_r, -self.circle_r]
self.u_bounds = [self.circle_r, self.circle_r]
# 画图
self.plt_obj = plt
# 是否画图
self.is_plt_show = is_plt_show
# 画图格式
self.fontsize = 14
self.point_in_circle_format_string = 'go'
self.point_outside_format_string = 'r*'
if self.is_plt_show:
self.plt_obj.xlabel("x", fontsize=self.fontsize)
self.plt_obj.ylabel("y", fontsize=self.fontsize)
def generate_halton(self):
"""halton序列生成"""
sampler = self.qmc_obj.Halton(d=2, scramble=False, seed=10)
sample = sampler.random(n=self.points_number)
sample = self.qmc_obj.scale(sample, self.l_bounds, self.u_bounds)
if self.is_plt_show:
self.plt_obj.title(f"halton序列,总的点数:{self.points_number},圆的半径:{self.circle_r}", fontsize=self.fontsize)
return sample
def generate_sobol(self):
"""sobol序列生成"""
sampler = self.qmc_obj.Sobol(d=2, scramble=False, seed=10)
sample = sampler.random(n=self.points_number)
sample = self.qmc_obj.scale(sample, self.l_bounds, self.u_bounds)
if self.is_plt_show:
self.plt_obj.title(f"sobol序列,总的点数:{self.points_number},圆的半径:{self.circle_r}", fontsize=self.fontsize)
return sample
def monte_carlo(self, sample_value):
for i in range(self.points_number):
x = sample_value[i][0] # 产生随机数
y = sample_value[i][1]
if math.sqrt(x ** 2 + y ** 2) <= self.circle_r: # 点在圆内
self.point_in_circle += 1
if self.is_plt_show:
self.plt_obj.plot(x, y, self.point_in_circle_format_string)
else:
if self.is_plt_show:
self.plt_obj.plot(x, y, self.point_outside_format_string)
if self.is_plt_show:
self.plt_obj.show()
self.estimated_pi = 4.0 * self.point_in_circle / self.points_number
self.error = abs(self.real_pi - self.estimated_pi) / self.real_pi
self.print_result()
def print_result(self):
print(
f"总的点数self.points_number:{self.points_number},落在圆内的点数self.point_in_circle为:{self.point_in_circle}")
print(f"估计的pi值self.estimated_pi为:{self.estimated_pi},真实的pi值self.real_pi为:{self.real_pi}")
print(f"误差为self.error:{self.error}")
"""####################################################蒙特卡洛算法求单位圆面积##########################################"""
"""误差分析——采样数量与误差之间的关系 此时固定为r=10"""
error_list = []
points_number_list = range(50, 10000, 50)
for points_number in points_number_list:
monte_carlo_obj1 = MonteCarlo(points_number=points_number, circle_r=10, is_plt_show=False)
monte_carlo_obj1.monte_carlo()
error_list.append(monte_carlo_obj1.error)
plt.plot(points_number_list, error_list)
plt.xlabel("points_number")
plt.ylabel("error")
plt.title(f"r=10时采样数量与误差的关系")
plt.show()
"""end"""
"""误差分析——半径与误差之前的关系 此时固定为采样数量为1000"""
error_list = []
circle_r_list = range(1, 1000, 5)
for circle_r in circle_r_list:
monte_carlo_obj2 = MonteCarlo(points_number=1000, circle_r=circle_r, is_plt_show=False)
monte_carlo_obj2.monte_carlo()
error_list.append(monte_carlo_obj2.error)
plt.plot(circle_r_list, error_list)
plt.xlabel("circle_r")
plt.ylabel("error")
plt.title(f"采样数量为1000时半径r与误差的关系")
plt.show()
"""end"""
"""####################################################end###########################################################"""
"""####################################################拟蒙特卡洛算法求单位圆面积##########################################"""
"""haltonx序列"""
"""误差分析——采样数量与误差之间的关系 此时固定为r=10"""
error_list = []
points_number_list = range(50, 10000, 50)
for points_number in points_number_list:
QuasiMonteCarlo_obj1 = QuasiMonteCarlo(points_number=points_number, circle_r=10, is_plt_show=False)
value = QuasiMonteCarlo_obj1.generate_halton()
QuasiMonteCarlo_obj1.monte_carlo(sample_value=value)
error_list.append(QuasiMonteCarlo_obj1.error)
plt.plot(points_number_list, error_list)
plt.xlabel("points_number")
plt.ylabel("error")
plt.title(f"halton序列,r=10时采样数量与误差的关系")
plt.show()
"""end"""
"""误差分析——半径与误差之前的关系 此时固定为采样数量为1000"""
error_list = []
circle_r_list = range(1, 1000, 5)
for circle_r in circle_r_list:
QuasiMonteCarlo_obj2 = QuasiMonteCarlo(points_number=1000, circle_r=circle_r, is_plt_show=False)
value = QuasiMonteCarlo_obj2.generate_halton()
QuasiMonteCarlo_obj2.monte_carlo(sample_value=value)
error_list.append(QuasiMonteCarlo_obj2.error)
plt.plot(circle_r_list, error_list)
plt.xlabel("circle_r")
plt.ylabel("error")
plt.title(f"halton序列,采样数量为1000时半径r与误差的关系")
plt.show()
"""end"""
"""sobol序列"""
"""误差分析——采样数量与误差之间的关系 此时固定为r=10"""
error_list = []
points_number_list = range(50, 10000, 50)
for points_number in points_number_list:
QuasiMonteCarlo_obj3 = QuasiMonteCarlo(points_number=points_number, circle_r=10, is_plt_show=False)
value = QuasiMonteCarlo_obj3.generate_sobol()
QuasiMonteCarlo_obj3.monte_carlo(sample_value=value)
error_list.append(QuasiMonteCarlo_obj3.error)
plt.plot(points_number_list, error_list)
plt.xlabel("points_number")
plt.ylabel("error")
plt.title(f"sobol序列,r=10时采样数量与误差的关系")
plt.show()
"""end"""
"""误差分析——半径与误差之前的关系 此时固定为采样数量为1000"""
error_list = []
circle_r_list = range(1, 1000, 5)
for circle_r in circle_r_list:
QuasiMonteCarlo_obj4 = QuasiMonteCarlo(points_number=1000, circle_r=circle_r, is_plt_show=False)
value = QuasiMonteCarlo_obj4.generate_sobol()
QuasiMonteCarlo_obj4.monte_carlo(sample_value=value)
error_list.append(QuasiMonteCarlo_obj4.error)
plt.plot(circle_r_list, error_list)
plt.xlabel("circle_r")
plt.ylabel("error")
plt.title(f"sobol序列,采样数量为1000时半径r与误差的关系")
plt.show()
"""end"""
"""####################################################end###########################################################"""
本文来自博客园,作者:JaxonYe,转载请注明原文链接:https://www.cnblogs.com/yechangxin/articles/17017600.html
侵权必究



 浙公网安备 33010602011771号
浙公网安备 33010602011771号