python实现汉诺塔问题——递归的使用例子

目录

• 汉诺塔问题是什么
• python代码实现
• 结论

汉诺塔问题是什么

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

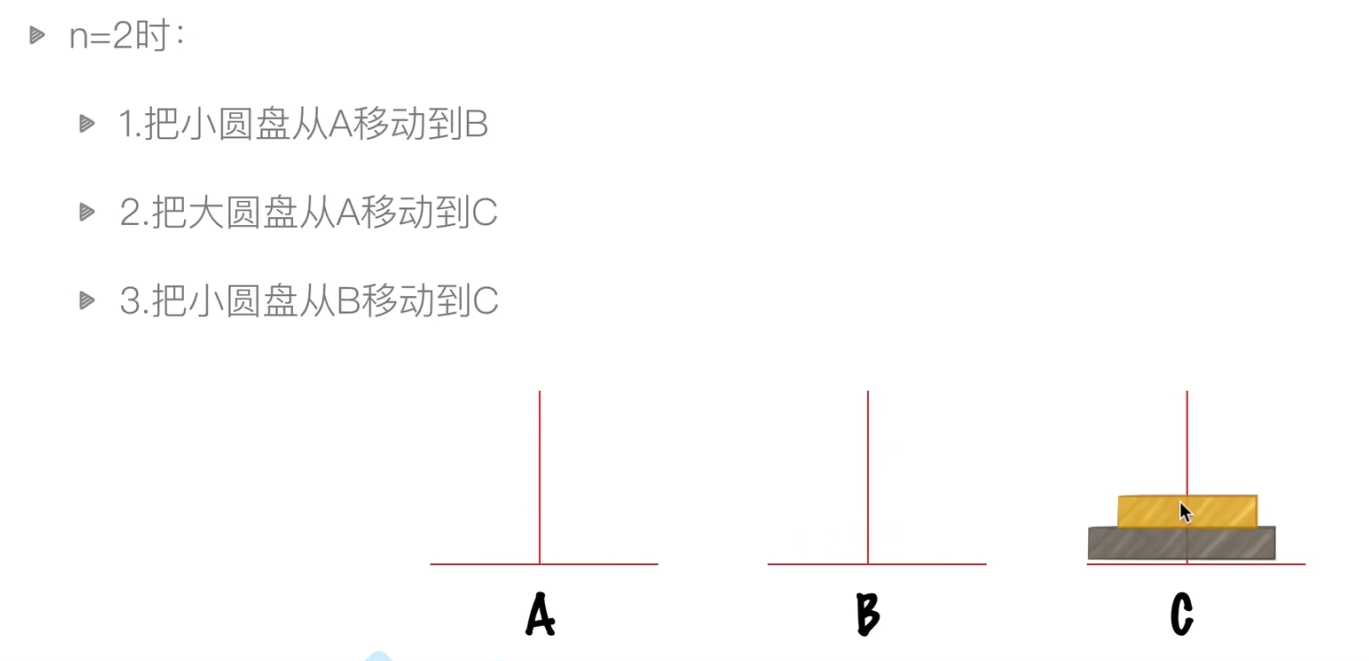
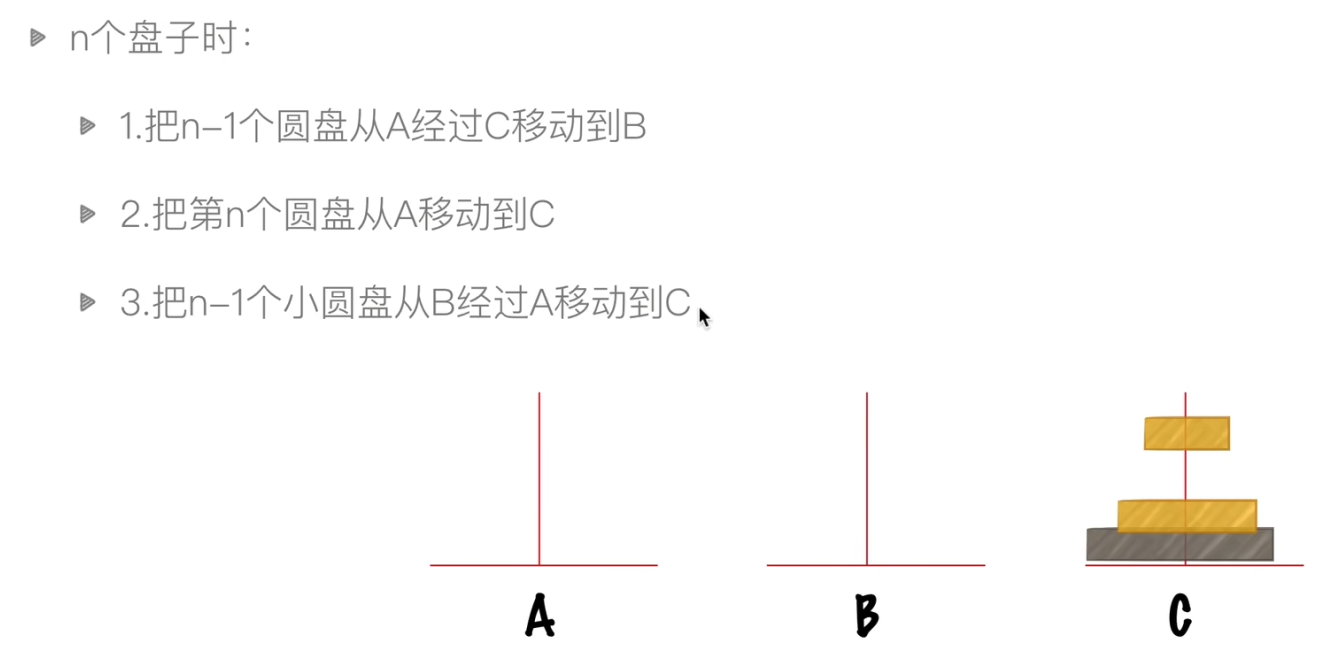
python代码实现

"""
汉诺塔问题
"""


def hanoi(n, a, b, c):
    """
    n为盘子数量，a、b、c表示从左到右的3条杆子。
    表示把n个盘子从a经过b移动到c !!!!!!
    """
    global step_time
    # 终止条件是n个盘子已经全部移动到c了，也就是只剩n=0个盘子了
    if n > 0:
        hanoi(n - 1, a, c, b)  # 表示把n-1个盘子从a经过c移动到b
        # print(f"从{a}移动到{c}")
        step_time = step_time + 1
        hanoi(n - 1, b, a, c)  # 表示把n-1个盘子从b经过a移动到c


step_time = 0
n = [1, 2, 3, 4, 5, 6, 10, 20]
# n = [64]
for i in n:
    hanoi(n=i, a='A', b='B', c='C')
    print(f"n={i}个盘子需要移动：{step_time}步")

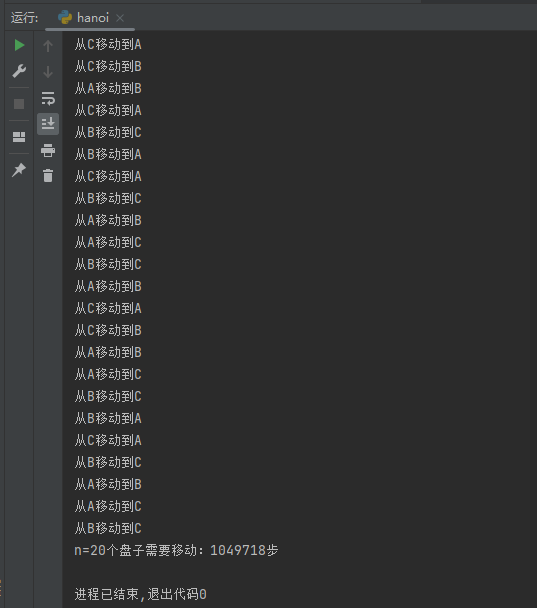
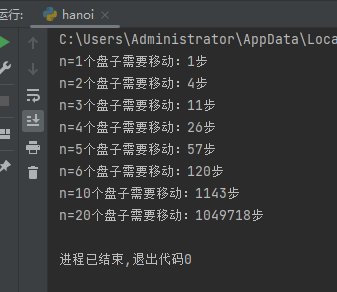
结论

可以看到，汉诺塔问题假设是一次移动一步的话，问题规模会爆炸性递增

也就是说算法的时间复杂度是2的n次方左右