《高级数据结构与算法设计》-第一章-导言算法笔记

《高级数据结构与算法设计》-第一章-导言算法

《高级数据结构与算法设计》-第一章-导言算法

@Author : ChangXin Ye

@Date : 2022年11月

@Description:《高级数据结构与算法设计》课程第一章笔记

@Version: v1.0

1、算法的概念

1.1 算法的定义

算法是一系列解决问题的明确指令，也就是说，对应符合一定规范的输出，能够在有限时间内获得要求的输出。程序=数据结构+算法。

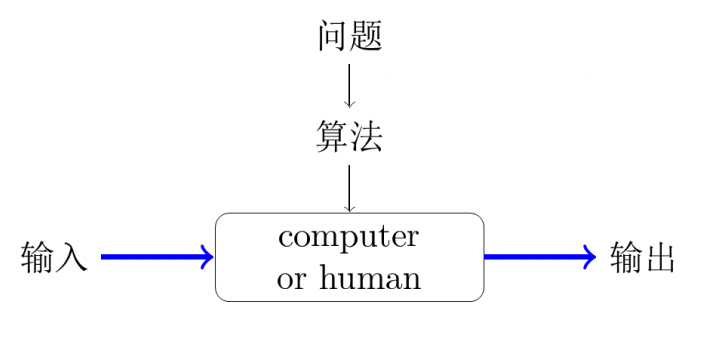
1.2 算法的特点

算法输入的值域是确定的
每一个步骤都可以清晰没有歧义
同一个算法可以有不同的形式来描述
同一个问题可以存在不同的算法
不同的算法对应于不同的解题思路，结题速度（或耗费的资源）可能存在差异

1.3 算法设计实施实例——最大公约数gcd(m,n)

1.3.1 关于最大公约数的课堂讨论

答：没有构成一个算法的描述，因为实现步骤不够清晰，例如没有说明如何找出质因数，没有说明找出公因数。

1.3.2 欧几里得的几何原本对最大公约数的描述

1.3.3 基于python的求最大公约数代码实现

class GcdAlgorithm(object):
    def __init__(self, m, n):
        self.m = max(m, n)
        self.n = min(m, n)

    def gcd_euclid(self):
        """欧几里得法"""
        m = self.m
        n = self.n
        r = m % n
        while r != 0:
            m = n
            n = r
            r = m % n
        print(f"{self.m}和{self.n}的最大公约数为:{n}")
        return n

    def other_way(self):
        pass


gcd_obj = GcdAlgorithm(m=60, n=24)
gcd_obj.gcd_euclid()

输出：60和24的最大公约数为:12

1.3.4 算法的可视化

即使用一些点、线段、各种曲线图的方式表现出算法操作中的一些“令人关注”的结果。

可视化的作用：

可作为算法效果展示
方便发现Bug

2、数据结构

2.1 数据结构的概念

数据结构是计算机中存储、组织数据的方式，程序=数据结构+算法。

2.2 数据结构的三要素

数据的逻辑结构：数据元素之间的逻辑关系，即从逻辑关系上描述数据。
数据的存储结构：数据结构在计算机中的表示（又称映像），也称物理结构。
数据的运算：施加在数据上的运算包括运算的定义何实现。

2.3 基本的数据结构

2.3.1 数组（Array）

2.3.2 堆栈（Stack）

一句话说，就是先进后出

2.3.2.1 基于python的list实现栈

"""python 列表实现栈"""
 
 
class Stack(object):
    def __init__(self):
        self.stack_list = []
 
    """入栈 压入栈底 即把新的元素加到列表尾部"""
    def push(self, item):
        self.stack_list.append(item)
 
    """出栈 后进先出 即把列表的最后一个元素移除 -1在python一般用于索引最后一位"""
    def pop(self):
        if self.is_empty_stock():
            print("栈为空，无法再进行出栈操作！")
            raise "栈为空，无法再进行出栈操作！"
        else:
            _temp_top_value = self.stack_list.pop()
            return _temp_top_value
 
    """获取栈顶的元素"""
    def get_top(self):
        if self.is_empty_stock():
            print("栈为空，无法获取栈顶元素！")
            raise "栈为空，无法获取栈顶元素！"
        else:
            return self.stack_list[-1]
 
    """判断栈是否空，即判断列表是不是空列表"""
    def is_empty_stock(self):
        return self.stack_list == []
 
    """栈的元素个数 即列表的长度"""
    def size(self):
        return len(self.stack_list)
 
 
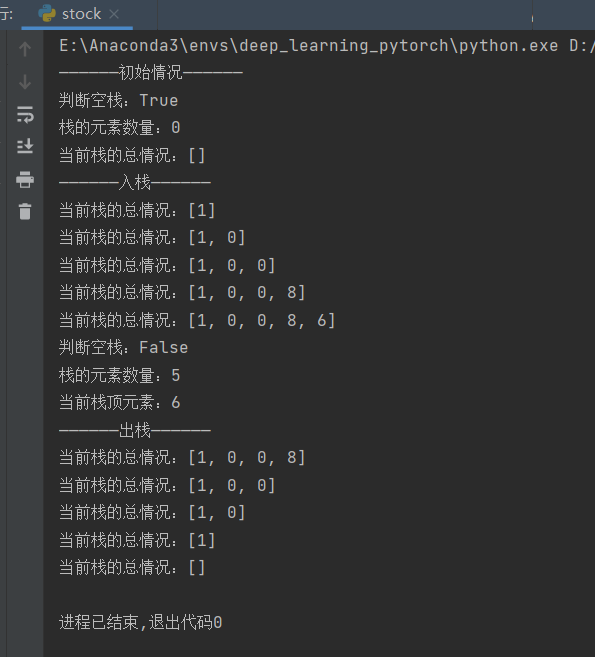
if __name__ == "__main__":
    stock1 = Stack()
    print("——————初始情况——————")
    print(f"判断空栈：{stock1.is_empty_stock()}")
    print(f"栈的元素数量：{stock1.size()}")
    # print(f"当前栈顶元素：{stock1.peek()}")
    print(f"当前栈的总情况：{stock1.stack_list}")
 
    # 入栈
    print("——————入栈——————")
    stock1.push(1)
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.push(0)
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.push(0)
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.push(8)
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.push(6)
    print(f"当前栈的总情况：{stock1.stack_list}")
    print(f"判断空栈：{stock1.is_empty_stock()}")
    print(f"栈的元素数量：{stock1.size()}")
    print(f"当前栈顶元素：{stock1.get_top()}")
 
    # 出栈
    print("——————出栈——————")
    stock1.pop()
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.pop()
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.pop()
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.pop()
    print(f"当前栈的总情况：{stock1.stack_list}")
    stock1.pop()
    print(f"当前栈的总情况：{stock1.stack_list}")
    # stock1.pop()
    # print(f"当前栈的总情况：{stock1.stack_list}")

2.3.3 队列（Queue）

一句话说，就是先进先出

2.3.3.1 基于python的list实现队列

"""python 列表实现队列"""
 
 
class Queue(object):
    def __init__(self):
        self.queue_list = []
 
    """入队  即把新的元素加到列表尾部"""
    def enqueue(self, item):
        self.queue_list.append(item)
 
    """出队 先进先出 即把列表的第一个元素移除"""
    def dequeue(self):
        if self.is_empty_queue():
            print("队列为空，无法再进行出队操作！")
            raise "队列为空，无法再进行出队操作！"
        else:
            _temp_head_value = self.queue_list.pop(0)
            return _temp_head_value
 
    """读取队头元素"""
    def get_head(self):
        if self.is_empty_queue():
            print("队列为空，无法获取队头元素！")
            raise "队列为空，无法获取队头元素！"
        else:
            return self.queue_list[0]
 
    """判断队列是否空，即判断列表是不是空列表"""
    def is_empty_queue(self):
        return self.queue_list == []
 
    """队列的元素个数 即列表的长度"""
    def size(self):
        return len(self.queue_list)
 
 
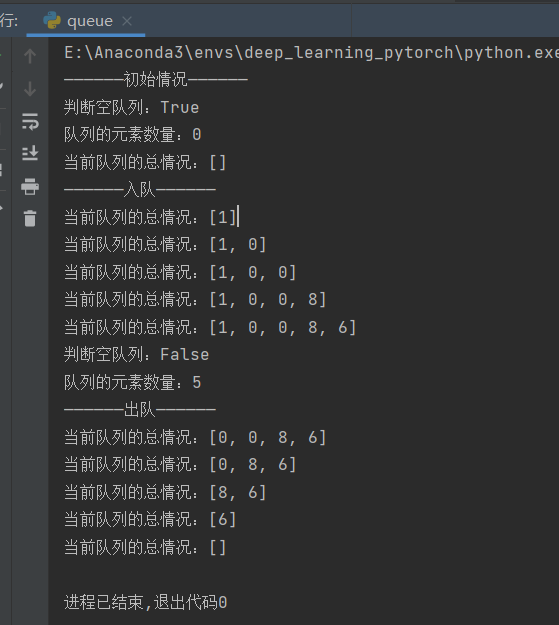
if __name__ == "__main__":
    queue = Queue()
    print("——————初始情况——————")
    print(f"判断空队列：{queue.is_empty_queue()}")
    print(f"队列的元素数量：{queue.size()}")
    print(f"当前队列的总情况：{queue.queue_list}")
 
    # 入队
    print("——————入队——————")
    queue.enqueue(1)
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.enqueue(0)
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.enqueue(0)
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.enqueue(8)
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.enqueue(6)
    print(f"当前队列的总情况：{queue.queue_list}")
    print(f"判断空队列：{queue.is_empty_queue()}")
    print(f"队列的元素数量：{queue.size()}")
 
    # 出队
    print("——————出队——————")
    queue.dequeue()
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.dequeue()
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.dequeue()
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.dequeue()
    print(f"当前队列的总情况：{queue.queue_list}")
    queue.dequeue()
    print(f"当前队列的总情况：{queue.queue_list}")

2.3.4 链表（Linked List）

2.3.5 树（Tree）

2.3.6 图（Graph）

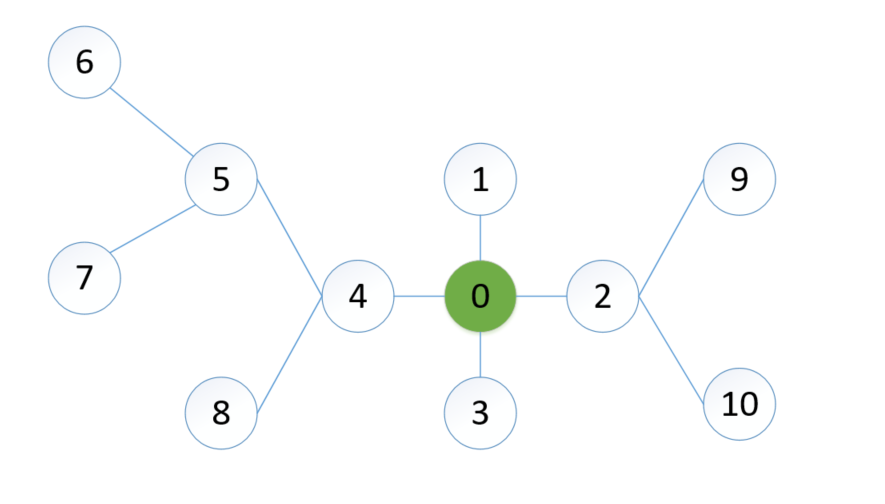
图最基本的问题是图的遍历问题，而图的遍历一般可分为深度优先遍历（DFS）和广度优先遍历（BFS）两种方法。

以该图为例，对DFS和BFS进行代码实现：

注：下面import的Stack和Queue就是2.3.2和2.3.3的代码

2.3.6.1 基于python实现图的深度优先遍历（DFS）

# encoding=utf-8
from data_structures_and_algorithms.stock import Stack
"""
深度优先遍历 基于栈
"""
def DFS(graph, starting_point):
    dfs_stock_obj = Stack()  # 主栈
    node_stock_obj = Stack()  # 主栈节点的子节点栈对象
    dfs_stock_obj.push(starting_point)
    used_points_list = []  # 记录已经遍历过的点
    used_points_list.append(starting_point)
    while not dfs_stock_obj.is_empty_stock():  # 一直到所有子、根节点遍历完一次
        _temp_top_value = dfs_stock_obj.pop()  # 取出栈顶元素并删掉，即列表最后一个元素
        node_stock_obj.stack_list = graph[_temp_top_value]
        for j in range(node_stock_obj.size()):  # 有几个子节点就遍历几次
            i = node_stock_obj.get_top()  # 取子节点栈顶，列表最后一位
            if i not in used_points_list:
                dfs_stock_obj.push(i)
                used_points_list.append(i)
            node_stock_obj.pop()
        print(_temp_top_value)
 
 
if __name__ == '__main__':
    graph = {
        "0": ["1", "2", "3", "4"],
        "1": ["0"],
        "2": ["0", "9", "10"],
        "3": ["0"],
        "4": ["0", "5", "8"],
        "5": ["4", "6", "7"],
        "6": ["5"],
        "7": ["5"],
        "8": ["4"],
        "9": ["2"],
        "10": ["2"],
    }
    print("深度优先遍历:")
    DFS(graph, '0')

2.3.6.2 基于python实现图的广度优先遍历（BFS）

from data_structures_and_algorithms.my_queue import Queue
"""
广度优先遍历
"""
 
def BFS(graph, starting_point):  # 广度优先遍历,基于队列
    bfs_queue_obj = Queue()  # 主队列
    node_queue_obj = Queue()  # 主队列元素下的子队列
    bfs_queue_obj.enqueue(starting_point)
    used_points_list = []  # 记录已经遍历过的点
    used_points_list.append(starting_point)
    while not bfs_queue_obj.is_empty_queue():  # 一直到所有子、根节点遍历完一次
        _temp_head_value = bfs_queue_obj.dequeue()  # 队列先进先出
        node_queue_obj.queue_list = graph[_temp_head_value]
        for j in range(node_queue_obj.size()):  # 有几个子节点就遍历几次
            i = node_queue_obj.get_head()  # 取子节点队头，列表第一位
            if i not in used_points_list:
                bfs_queue_obj.enqueue(i)
                used_points_list.append(i)
            node_queue_obj.dequeue()
        print(_temp_head_value)
 
 
if __name__ == '__main__':
    graph = {
        "0": ["1", "2", "3", "4"],
        "1": ["0"],
        "2": ["0", "9", "10"],
        "3": ["0"],
        "4": ["0", "5", "8"],
        "5": ["4", "6", "7"],
        "6": ["5"],
        "7": ["5"],
        "8": ["4"],
        "9": ["2"],
        "10": ["2"],
    }
    print("广度优先遍历:")
    BFS(graph, '0')

2.3.7 堆（Heap）

2.3.8 散列表（Hash）

2.4 数据结构与算法效率的例子

需求：在一个线性结构的首部插入一个新元素

数组：需要把所有元素复制，对于大规模数据很慢

链表：可以快速插入，与规模无关

3、主要问题的类型

3.1 排序

按照升序或降序重新排雷指定列表中的数据项

常见的排序算法有：

冒泡排序
插入排序
快速排序
......

基于“键”比较的排序算法最快的需要$$nlog_{2} n$$次比较可以完成长度为n的任意数组的排序

\[nlog_{2} (n!) \thickapprox nlog_{2} (\sqrt{2\pi n}(\frac{n}{e})^n) \]

当n很大时

\[nlog_{2} (n!) \thickapprox nlog_{2} (\sqrt{2\pi n}(\frac{n}{e})^n) \thickapprox nlog_{2} (n) \]

3.2 查找

在给定的集合找出一个给定的值

常见的查找方法：

顺序搜索
二分查找
Hash查找
......

3.3 字符串处理

字母表中符号构成的序列

例如：

0101010abcABC
"hello world 你好世界"
......

3.4 图问题

一些顶点构成的集合，其中某些顶点由边连接。现实例子：交通、通信、社会、经济网络。

常见关于图的问题和算法：

遍历算法
最短路径算法
有向图的拓扑排序算法
旅行商问题（TSP）：找出访问n个城市的最短路径并返回源点，每个城市只能访问一次。
图填色问题
......

3.5 组合问题

寻找一个排列、一个组合、或一个子集，这个解能够满足特定条件并具有我们想要的特性，如价值最大化或成本最小化。

最著名的组合问题：

TSP问题
SAT：逻辑变量的复合语句，求使其为真的变量值
NLP：非线性规划
......

3.6 几何问题

处理类似于点、线、面这样子的几何对象，应用于计算机图形学、机器人、断层X射线摄像

常见几何问题：

最近邻问题：寻找n个点中距离指定位置最近的点
最近对问题：寻找平面上n个点中距离最近的2个点
凸包问题：寻找一个可以把给定集合中的点包含的最小凸多边形
几何变换：平移、旋转、镜像等
.......

3.7 数值问题

数值问题实例：

解方程（求根）
计算定积分
计算函数的值
最优化问题
......

4、时间和空间复杂度——“鱼和熊掌不可兼得”

复杂度可以度量算法效率：

时间复杂度可以衡量算法运行有多快
空间复杂度可以衡量算法需要的存储空间有多少

4.1 时间复杂度

为什么衡量算法运行速度要用时间复杂度描述，而不是用代码运行时间描述？

每台机器由于性能等各方面不一样，代码运行时间是不一样的，这样子就很难比较算法的好坏了，所以引入了时间复杂度的概念。

常见的时间复杂度量级	时间复杂度	例子	时间复杂度比较	说明
常数阶	$$O(1)$$	`int i = 1;` `int j = 2;` `++i;` `j++;` `int m = i + j;`	最小	无论代码执行了多少万行，只要是没有循环等复杂结构，正确的表示方法是，这个代码的时间复杂度就都是$$O(1)$$
对数阶	$$O(log_2n)$$	`int i = 1;` `while(i<n)` `{i = i * 2;};`	$\wedge$	从1开始，每次都将 i 乘以 2第一次i=1*2=2^1，那么那么乘了x次就是循环了x次， $$这个时候i=2^x，令其=n，则x=log_2n$$了
线性阶	$$O(n)$$	`for(i=1; i<=n; ++i)` `{里面默认常数阶}`	$\wedge$	for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的
线性对数阶	$$O(nlog_2n)$$	`for(i=1; i<=n; ++i)` `{` `int i = 1;` `while(i<n)` `{i = i * 2;}` `};`	$\wedge$	其实就是线性阶和对数阶的嵌套
平方阶	$$O(n^2)$$	`for(i=1; i<=n; ++i)` `{` `for(i=1; i<=n; ++i)` `{里面默认常数阶}` `}`	$\wedge$	显然，是线性阶嵌套吧，嵌套层数是2层
立方阶	$$O(n^3)$$	按照平方阶的思维去理解	$\wedge$	按照平方阶的思维去理解，立方阶显然是线性阶嵌套了3层的意思
指数阶	$$O(2^n)$$	`int aFunc(int n) {` `if (n <= 1)` `return 1;` `else` `return aFunc(n - 1) + aFunc(n - 2);` `}`	$\wedge$	斐波那契数列解法之一，通过归纳证明法可以证明
n的阶乘阶	$$O(n!)$$	`def factorial(n):{` `for i in range(n):` `factorial(n-1)}`	$\wedge$	比n的n次方阶区别是嵌套的迭代次数慢慢减1了
n的n次方阶	$$O(n^n)$$	按照平方阶的思维去理解	$\wedge$	按照平方阶的思维去理解，n的n次方阶显然是线性阶嵌套了n层的意思

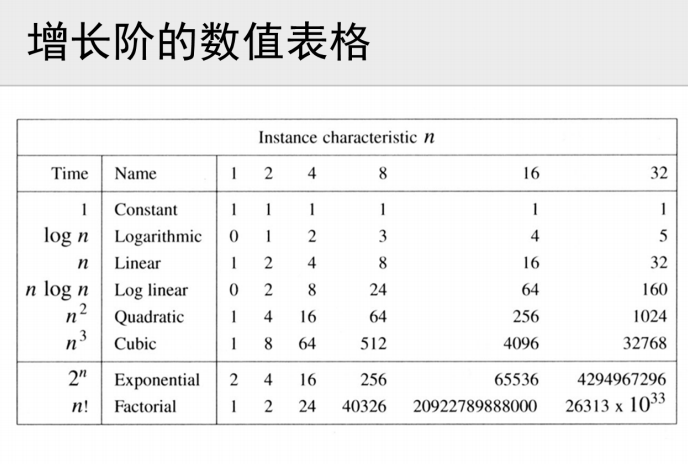
多项式的次数最好不要大于3阶！

4.2 空间复杂度

比起空间复杂度，我们更关心时间复杂度。

5 延伸讨论——P=NP ？

5.1可计算性

一个问题是否可以被计算机描述并解决。

5.2 图灵停机问题

停机问题就是判断任意一个程序是否能在有限的时间之内结束运行的问题。

等价于如下判别问题：

是否存在一个程序P，对于任意输入的程序w，能够判断w会在有限时间内结束或者无限循环。

考虑如下程序w：

若P(w)的判断结果为真，则进入无限循环
若P(w)的判断结果为假，则立即结束

因此，P无法判定w是否停机。

就像理发师悖论中，理发师该不该给他自己刮胡子一样, 将陷入两难境地

5.3 判决问题和非判决问题

5.3.1 判决问题

对于给定的输入，输出Yes或No的问题，例如

判定一个数是否是质数？
判定一个图上是否有从s到t的路径？
判定一个图上是否有回路？

5.3.2 非判决问题

例如

找到图上有从s到t的（最短）路径
找到给定整数的（最大）质因数

5.3.3 非判决问题转为一系列判决问题

例如对于非判决问题：找到图中从s到t的最短路径长度？可以引入额外的参数k进行判决：

对k=1，是否存在不超过k的从s到t的路径
对k=2，是否存在不超过k的从s到t的路径
对k=3，是否存在不超过k的从s到t的路径
......

如果对转换得到的判决性问题都没有低复杂度的算法，那通常也很难找到原始非判决问题的低复杂度算法。

5.4 判决性问题的分类

P问题是所有的可以在最多多项式时间复杂度上解决的判决问题

例如：Z是否是x和y的公约数？
NP问题是所有的可以在多项式时间复杂度上验证解的正确性的判决问题

可以快速（多项式时间）给出yes的回答

对yes的情况，能够快速“猜”到；对no的情况则随机猜测

如果yes的情况“猜”对后能快速判定

可求解隐含可验证，因此$$P \subseteq NP$$

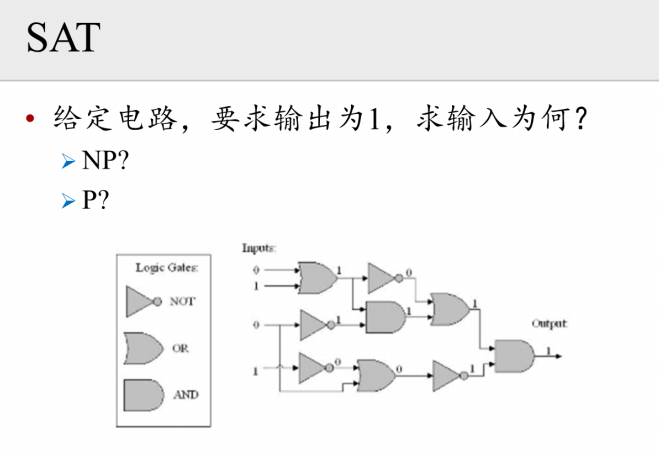
对于SAT，起码是个NP问题。

5.5 规约/约化

规约的概念：若问题A（更简单）可以用多项式的时间转换为问题B（更难），解决B即可解决A，则称A可以规约B。

直观意义：用一个更复杂度的方法才能去解决简单问题，也就是说，问题A不比问题B难。

那么，按照上述过程一直规约下去，可以直到找到NP里面最难的问题

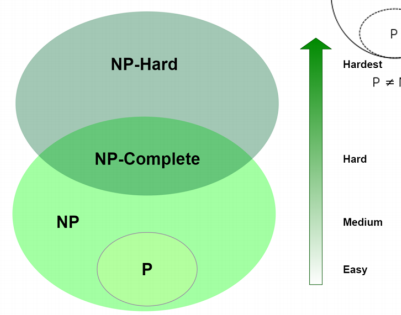
5.6 NP-Complete问题

NP-完全问题，所有NP问题中最难的问题，其他NP问题都可以规约为这些问题。

需同时满足下面两个条件：

它是一个NP问题
已知的NPC问题能约化到它

目前已经证明——所有的NP问题可以规约为SAT问题。

当我们发现我们的问题达到了NPC问题，基本上可以考虑放弃，或者采取近似的方式逼近，允许一定的误差。

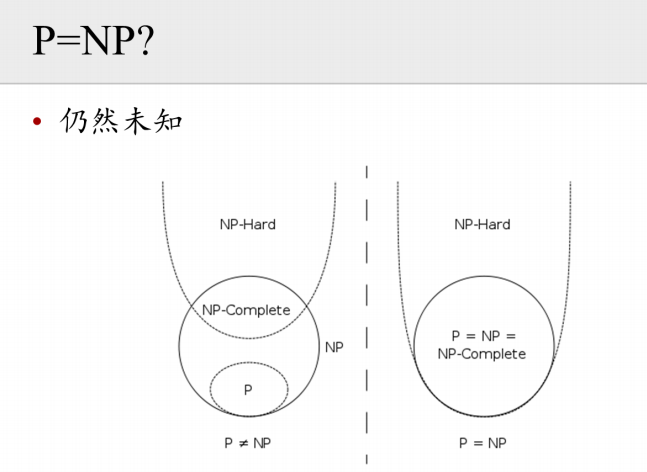
目前来看，P和NP是否等于还不确定。

5.7 NP-hard 问题

至少有NP-Complete的难度，可能还会更难一些，但是不要求是NP问题。

5.8 案例——TSP问题

TSP decision problem——对于图G，是否存在最长不超过b的环游？
- 是判决问题，达到了NPC的难度，已经没有多项式解法了。
TSP search problem——对于图G，找到一条长度不超过b的环游？
- 问题更难了一点
TSP optimization problem——对于图G，找到长度最短的环游？
- NP-hard

posted @ 2022-11-12 17:06 JaxonYe 阅读(58) 评论(0) 收藏举报

刷新页面返回顶部

Jaxon的官方博客

版权所有，转载请注明出处

《高级数据结构与算法设计》-第一章-导言 算法 笔记

《高级数据结构与算法设计》-第一章-导言 算法