KNN算法

目录

• KNN算法
  • 1、概念
  • 2、基本原理
  • 3、距离度量
    • 3.1 欧式距离（欧几里得距离）
    • 3.2 曼哈顿距离
  • 4、K值选择
  • 5、KNN特点
    • 5.1 优点
    • 5.2 缺点

KNN算法

参考：csdn-KNN算法风凌天下，主要是对其文章进行了复述理解。

1、概念

KNN算法，又叫k近邻法（k-nearest neighbor，k-NN），k个最近的邻居，即每个样本都可以用它最接近的k个邻居来代表。是一种基本的分类和回归方法，是监督学习方法里的一种常用方法。

2、基本原理

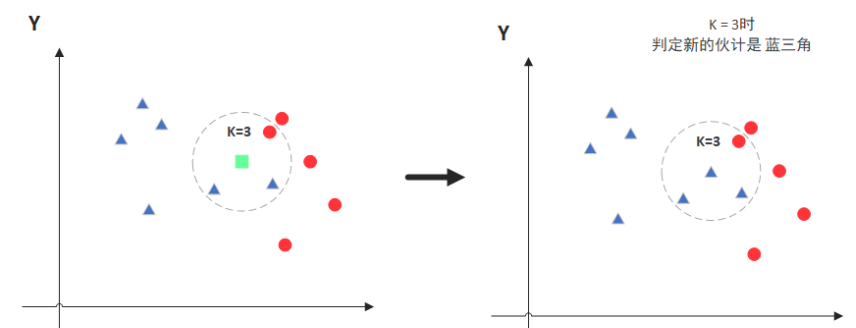
当k=3时，圈中有2个蓝色，1个红色，所以把绿色的点归类为蓝色。

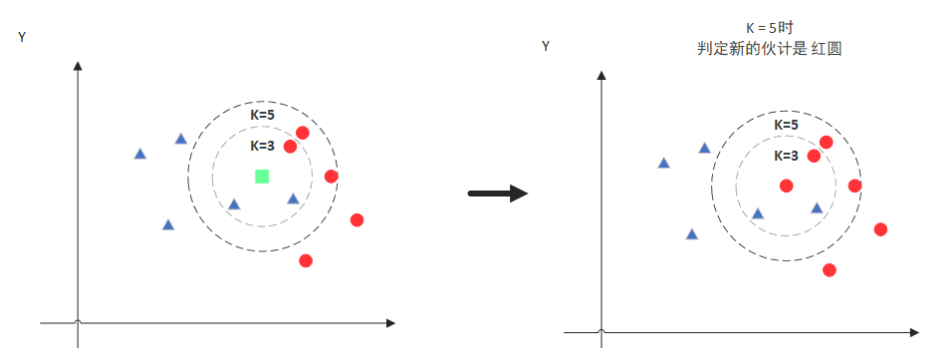
当k=5时，圈中有2个蓝色，3个红色，所以把绿色的点归类为红色。

那么，如何进行K值的选取和点距离的计算呢？

3、距离度量

主要是欧式距离和曼哈顿距离用得多一点

3.1 欧式距离（欧几里得距离）

连接两点的线段的长度，多维类推

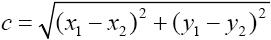
3.2 曼哈顿距离

多维类推

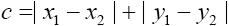
4、K值选择

通过交叉验证（将样本数据按照一定比例，拆分出训练用的数据和验证用的数据，比如6：4拆分出部分训练数据和验证数据），从选取一个较小的K值开始，不断增加K的值，然后计算验证集合的方差，最终找到一个比较合适的K值。
例如：

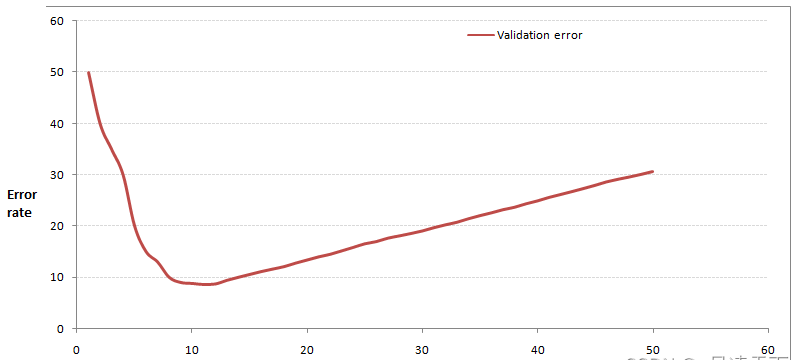
当你增大k的时候，一般错误率会先降低，因为有周围更多的样本可以借鉴了，分类效果会变好。但注意，和K-means不一样，当K值更大的时候，错误率会更高。这也很好理解，比如说你一共就35个样本，当你K增大到30的时候，KNN基本上就没意义了。

5、KNN特点

非参的：这个模型不会对数据做出任何的假设，与之相对的是线性回归（我们总会假设线性回归是一条直线）
惰性的：同样是分类算法，逻辑回归需要先对数据进行大量训练（tranning），最后才会得到一个算法模型。而KNN算法却不需要，它没有明确的训练数据的过程，或者说这个过程很快。

5.1 优点

简洁明了、模型训练时间快

5.2 缺点

对内存要求较高，因为该算法存储了所有训练数据