DS博客作业03--树

0.PTA得分截图

1.本周学习总结（0-5分）

1.1 总结树及串内容

1.1.1 串

• 串的定义：
  串(string)是n个字符的有序数列。通常记作s=‘a1a2a3····an’（n>0）（s为串名，单引号中的字符序列为串的值）
• 串的存储结构：
  1.静态存储结构：将串定义为字符型数组，数组名救赎串名，串的存储空间分配在编译时完成，程序运行时不能更改。
  2.动态存储结构：定义字符指针变量，存储串值的首地址，通过字符指针变量名访问串值，串的存储空间分配是在程序运行时动态分配的。
• 串的基本运算

StrAssign(&s,cstr)：将字符串常量cstr赋给串s，即生成其值等于cstr的串s。

StrCopy(&s,t)：串复制。将串t赋给串s。

StrEqual(s,t)：判串相等。若两个串s与t相等则返回真；否则返回假。

StrLength(s)：求串长。返回串s中字符个数。

Concat(s,t)：串连接:返回由两个串s和t连接在一起形成的新串。

SubStr(s,i,j)：求子串。返回串s中从第i（1≤i≤n）个字符开始的、由连续j个字符组成的子串。

InsStr(s1,i,s2)：插入。将串s2插入到串s1的第i（1≤i≤n+1）个字符中，即将s2的第一个字符作为s1的第i个字符，并返回产生的新串。

DelStr(s,i,j)：删除。从串s中删去从第i（1≤i≤n）个字符开始的长度为j的子串，并返回产生的新串。

RepStr(s,i,j,t)：替换。在串s中，将第i（1≤i≤n）个字符开始的j个字符构成的子串用串t替换，并返回产生的新串。

DispStr(s)：串输出。输出串s的所有元素值。

• C++中的字符串库（string）
  C++中加上头文件#include就可以用string定义字符串，并且运用到size(),length()，empty(),substr(),find(),compare(),append()等函数
• 串的模式匹配算法
  • BF算法(Brute-Force算法)：
    基本思路：将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较，直到得出最后的匹配结果。
    算法实现：

int BF(const char *str,const char *sub,int pos)
{
    assert(str!=NULL&&sub!=NULL);
    int i=pos;    //用i来记录S中字符的位置
    int j=0;    //用j来记录T中字符的位置
    int lens=strlen(str);
    int lensub=strlen(sub);    //当S不为空并且T不为空时，逐个进行字符的比较
    while(j<lensub&&i<lens)
    {
        if(str[i]==sub[i])    //当S中第i个字符与T中第j个字符相等时，i向后移一个，j向后移一个
        {
            i++;
            j++;
        }
        else    //当S中第i个字符与T中第i个字符不相等时，i回到前一个位置的下一个位置，j回到0号位置
        {
            i=i-j+1;
            j=0;
        }
    }
    if(j>=lensub)    //当j走完T的长度时，也就说明T在S中匹配成功
    {
        return i-j;    //此时返回字串在主串中的下标位置，此时i在该返回下标位置+j的长度位置，所以返回i-j，本例中返回下标3
    }
    else return -1;    //匹配失败，则返回-1，因为0下标存在，所以不能返回0下标
}

• KMP算法：
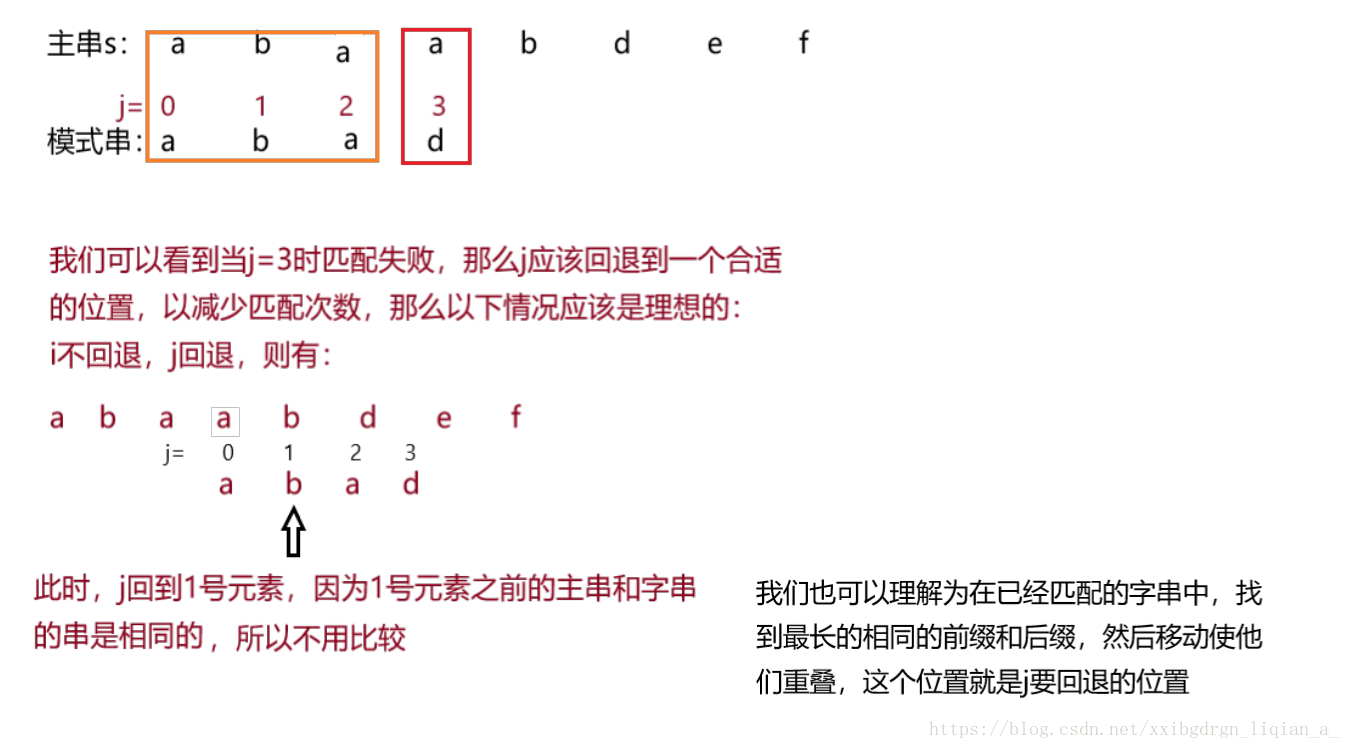
  基本思路：在KMP算法中，对于每一个模式串都会事先计算出模式串的内部匹配信息，在匹配失败时最大的移动模式串，以减少匹配次数，这样就很好的解决了BF算法的缺陷。比如，当匹配失败后，最好是能够将模式字串尽量的右移和主串进行匹配，右移的距离在KMP算法中是这样计算的：在已经匹配的字串中，找到最长的相同的前缀和后缀，然后移动使他们重叠，这个位置就是j要回退的位置，这样j就不用每一次都回到0号位置了，每一次j回退的位置存储在一个数组里，称之为next数组。如图：
  
  根据以上理论，我们求得模式串的next数组：
  
  代码实现：

void GetNext(int *next,const char *sub)
{
    next[0] = -1;
    next[1] = 0;
    int lensub = strlen(sub);
    int i = 2;//当前的i
    int k = 0;//前一项的K值
    while(i < lensub)
    {
        if(k == -1 || sub[i-1] == sub[k])
        {
            next[i] = k+1;
            i++;
            k = k+1;
        }
        else
        {
            k  = next[k];
        }
    }
}
int Kmp(const char *str,const char *sub,int pos)
{
    int i = pos;
    int j = 0;
    int lens = strlen(str);
    int lensub = strlen(sub);
    int *next = (int *)malloc(sizeof(int) * lensub);
    assert(next != NULL);
    GetNext(next,sub);
    while(j < lensub && i < lens)
    {
        if(j == -1 || str[i] == sub[j])
        {
            i++;
            j++;
        }
        else
        {
            j = next[j];
        }
    }
    if(j >= lensub)
    {
        return i-j;
    }
    else
    {
        return -1;
    }
}

1.1.2 二叉树

• 概念：
  一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
• 特点：
  1.每个结点最多有两棵子树，即二叉树不存在度大于2的结点。
  2.二叉树的子树有左右之分，其子树的次序不能颠倒。
• 满二叉树
  • 特点：
    1.所有分支结点都有双份结点
    2.叶结点都集中在二叉树的最下一层
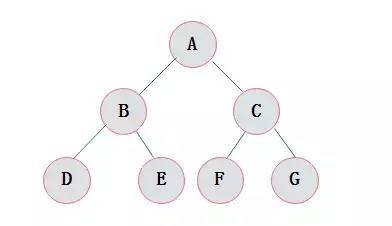
    3.高度为h的满二叉树恰好有2^h-1个结点
  • 显示图：
    
• 完全二叉树
  • 特点：
    1.最多只要下面两层的结点的度数小于2
    2.最下面一层的叶结点都依次排列在该层的最左边的位置上
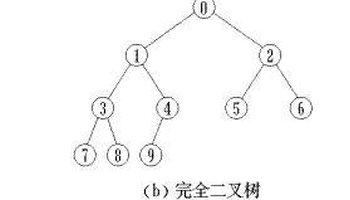
    3.完全二叉树实际上可以认为是对应的满二叉树删除叶结点层最右边若干个结点得到的
  • 显示图：
    
• 性质：
  1.在二叉树中的第i层上至多有2^(i-1)个结点（i>=1)。
  2.深度为k的二叉树至多有2^k - 1个节点（k>=1)。
  3.包含n个结点的二叉树的高度至少为log2 (n+1)
  4.对任何一棵二叉树T，如果其叶结点数目为n0，度为2的节点数目为n2，则n0=n2+1。
• 存储结构：
  • 顺序存储结构：
    顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储，二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。
    
  • 链式存储结构：
    二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址，链式结构又分为二叉链和三叉链
    
• 二叉树的建立：
  • 顺序存储结构建立二叉树：

BTree CreateBTree(string str,int i)
{
   int len;
   BTree bt;
   bt=new TNode;
   len=str.size();
   if(i>len || i<=0) return NULL;
   if(str[i]=='#') return NULL;
   bt->data =str[i];
   bt->lchild =CreateBTree(str,2*i); 
   bt->rchild =CreateBTree(str,2*i+1); 
   return bt;
}

• 先序递归建立二叉树：

BTree CreatTree(string str, int &i)
{
	BTree bt;
	if (i > len - 1) return NULL;
	if (str[i] == '#') return NULL;
	bt = new BTNode;
	bt->data = str[i];
	bt->lchild = CreatTree(str, ++i);
	bt->rchild = CreatTree(str, ++i);
	return bt;
}

• 二叉树的遍历：
  • 先序遍历：

void PreOrder(BTree bt)
{     if (bt!=NULL)  
      {     
             cout<<bt->data; 	//访问根结点
             PreOrder(bt->lchild);
             PreOrder(bt->rchild);
      }
}

• 中序遍历：

void InOrder(BTree bt)
{       if (bt!=NULL)  
        {      
         InOrder(bt->lchild);
	 cout<<bt->data; 	//访问根结点
	 InOrder(bt->rchild);
       }
}

• 后序遍历：

void PostOrder(BTree bt) 
{      if (bt!=NULL)  
        {      
         PostOrder(bt->lchild);
	 PostOrder(bt->rchild);
	 cout<<bt->data; 	//访问根结点
       }
}

1.1.3 树

• 相关名词解释：
  结点：指树中的一个元素；
  结点的度：指结点拥有的子树的个数，二叉树的度不大于2；
  数的度：指树中的最大结点度数；
  叶子：度为0的结点，也称为终端结点；
  高度：叶子节点的高度为1，根节点高度最高；
  层：根在第一层，以此类推；
• 概念：
  树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：每个结点有零个或多 个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结 点可以分为多个不相交的子树
• 二叉树与树的关系：
  二叉树是一种特殊的树，二叉树结点的度小于等于2
• 存储结构：
  • 双亲存储结构：

typedef struct 
{　 
     ElemType data;	//结点的值
　   int parent;		//指向双亲的位置
} PTree[MaxSize];
特点：从孩子结点找双亲结点易于从双亲结点找孩子结点

• 孩子链存储结构：

typedef struct node
{      
        ElemType data;		  //结点的值
        struct node *sons[MaxSons];	      //指向孩子结点
}  TSonNode;

特点：可能会出现许多空指针的情况，找孩子结点容易

• 孩子兄弟链存储结构:

typedef struct tnode 
{      
        ElemType data;	//结点的值
        struct tnode *son;  	//指向兄弟
        struct tnode *brother;  2//指向孩子结点
} TSBNode;

特点：每个结点固定只有两个指针域，类似二叉树，找双亲不易

• 树的遍历：
  • 定义：
    树的遍历运算是指按某种方式访问树中的每一个结点且每一个结点只被访问一次。
  • 先根遍历：
    若树不空，则先访问根结点，然后依次先根遍历各棵子树。
  • 后根遍历：
    若树不空，则先依次后根遍历各棵子树，然后访问根结点。
  • 层次遍历：
    若树不空，则自上而下、自左至右访问树中每个结点。

1.1.4 线索二叉树：

• 定义：
  n个结点的二叉链表中含有n+1(2n-(n-1)=n+1)个空指针域。利用二叉链表中的空指针域，存放指向结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索")。这种加上了线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树。
• 分类：
  根据线索性质的不同，线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
• 结构体定义：

typedef struct node 
  {      
         ElemType data;		//结点数据域
         int ltag，rtag;      		//增加的线索标记
         struct node *lchild;		//左孩子或线索指针
         struct node *rchild;		//右孩子或线索指针
  }  TBTNode;		　　//线索树结点类型定义 

• 结点操作：
  • 若结点有左子树，则lchild指向其左孩子；否则， lchild指向其直接前驱(即线索)；
  • 若结点有右子树，则rchild指向其右孩子；否则， rchild指向其直接后继(即线索) 。

1.1.5哈夫曼树：

• 定义
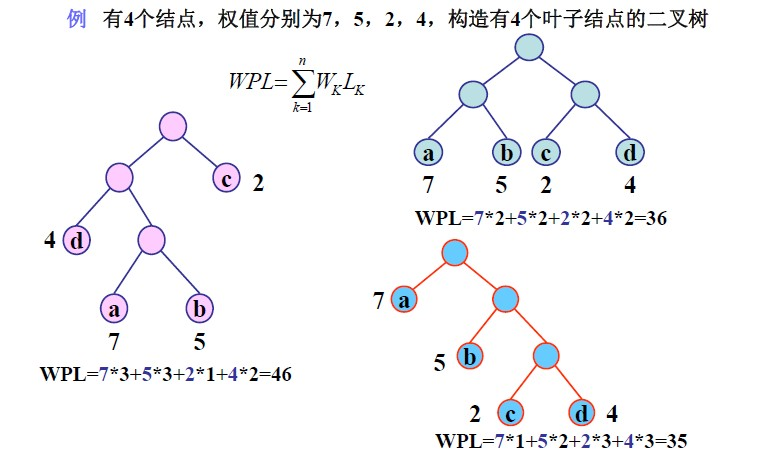
  假设有m个权值｛w1,w2,w3,...,wn｝，可以构造一棵含有n个叶子结点的二叉树，每个叶子结点的权为wi，则其中带权路径长度WPL最小的二叉树称做最优二叉树或哈夫曼树。
  例：
  
  第三种树的的带权路径长度WPL最小，所以第三种为哈夫曼树。
• 哈夫曼树的构建：
  根据哈弗曼树的定义，一棵二叉树要使其WPL值最小，必须使权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点。哈弗曼依据这一特点提出了一种构造最优二叉树的方法，其基本思想如下：
  
• 结点结构定义：

typedef struct {
    char data;//结点值
    int weight;//结点权重
    int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
}HTNode, *HuffmanTree;

1.1.6 并查集

• 定义：
  查找一个元素所属的集合及合并2个元素各自专属的集合等运算
• 并查集的操作：
  • 结构体定义：

typedef struct node
{
    int dada;    //结点对应人的编号
    int rank;    //结点秩：子树的高度，合并用
    int parent;    //结点对应双亲下标
}UFSTree;    

• 并查集树的初始化:

void MAKE_SET(UFSTree t[]，int n)  //初始化并查集树
{      
        int i;
        for (i=1;i<=n;i++)
        {	
            t[i].data=i;		//数据为该人的编号
	    t[i].rank=0;		//秩初始化为0
	    t[i].parent=i;		//双亲初始化指向自已
         }
}

• 查找一个元素所属的集合:

int FIND_SET(UFSTree t[], int x)
{    
     if(x!=t[x].parent)    //双亲不是自己
         return(FIND_SET(t, t[x].parent));    //递归在双亲中找x
     else   
         return(x);    //双亲是自己，返回x
}

• 两个元素各自所属的集合的合并:

void UNION(UFSTree t[], int x, int y)
{
    x=FIND_SET(t, x);
    y=FIND_SET(t, y);
    if(t[x].rank>t[y].rank)
        t[y].parent=x;
    else
    {
        t[x].parent=y;
        if(t[x].rank==t[y].rank)
            t[y].rank++;
    }
}

1.2 谈谈你对树的认识及学习体会。

在对树的学习之前，老师就曾提醒过，非线性结构存储类型会难于之前学过的线性结构存储类型，在这两周的学习中，渐渐明白了其中的困难，也深刻了要更加努力的想法。
在刚开始学习树时感觉内容会有点抽象，不过随着对树的不断编程应用，对树操作也熟络起来，逐渐对树的运行模式管中窥豹。
在对树的学习中，不断地运用着递归的方法，对递归的方法也不断熟络了起来。

2.阅读代码（0--5分）

2.1 题目及解题代码

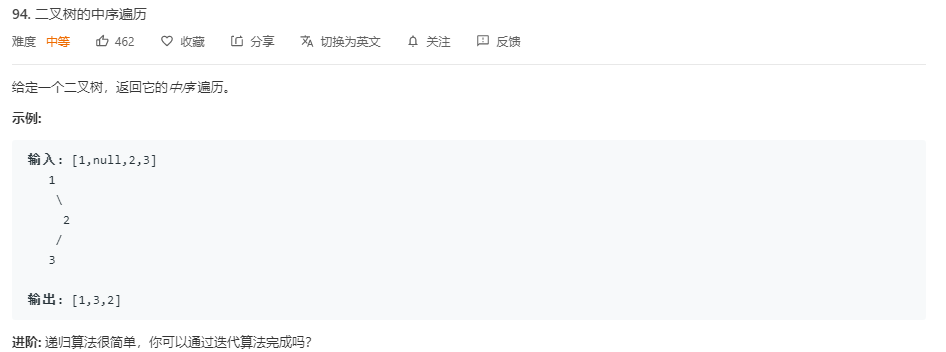
• 题目:
  
• 题解：

vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> S;
        vector<int> v;
        TreeNode* rt = root;
        while(rt || S.size()){
            while(rt){
                S.push(rt->right);
                v.push_back(rt->val);
                rt=rt->left;
            }
            rt=S.top();S.pop();
        }
        return v;        
    }

2.1.1 该题的设计思路

• 设计思路：
  每到一个节点 A，就应该立即访问它。
  因为，每棵子树都先访问其根节点。对节点的左右子树来说，也一定是先访问根。
  在 A 的两棵子树中，遍历完左子树后，再遍历右子树。
  因此，在访问完根节点后，遍历左子树前，要将右子树压入栈。
• 时间复杂度：O(n)
• 空间复杂度：O(n)

2.1.2 该题的伪代码

栈S;
rt= root;
while(rt || S不空){
    while(rt){
        访问rt节点；
        rt的右子树入S;
        rt = rt的左子树;
    }
    rt = S栈顶弹出;
}

2.1.3 运行结果:

2.1.4 分析该题目解题优势及难点:

• 迭代方法类似于递归，容易对我们近期常用递归的学生理解。
• 迭代方法又区别于递归，要理解运用还需加深学习，还需多加研究理解。

2.2 题目及解题代码

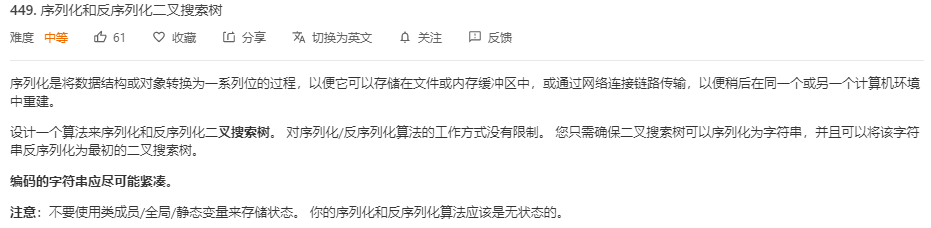
• 题目：
  

• 解题代码：

class Codec {
public:
    void num2str(int val,string& data)
    {
        string tmp;
        while(val)
        {
            tmp += val%10 + '0';
            val = val / 10;
        }
        for(int i=tmp.length()-1;i>=0;i--)
        {
            data += tmp[i];
        }
        data += "#" ; 

    }
    void BST_preorder(TreeNode*root,string& data)
    {
        if(!root)
        {
            return;
        }
        string str_val;
        num2str(root->val,str_val);
        data += str_val;
        BST_preorder(root->left,data);
        BST_preorder(root->right,data);
    }
    void BST_insert(TreeNode* root,TreeNode* insert_node)
    {
        if(root->val > insert_node->val)
        {
            if(root->left)
            {
                BST_insert(root->left,insert_node);
            }
            else
            {
                root->left=insert_node;
            }
        }else
        {
            if(root->right)
            {
                BST_insert(root->right,insert_node);
            }
            else
            {
                root->right=insert_node;
            }
        }
    }
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        std::string data;
        BST_preorder(root,data);
        return data;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        vector<TreeNode*> vec;
        int val=0;
        if(data.length() == 0)
        {
            return NULL;
        }
        for(int i=0;i<data.length();i++)
        {
            if(data[i] == '#')
            {
                vec.push_back(new TreeNode(val));
                val=0;
            }else
            {
                val=val*10 + data[i] - '0';
            }
        }
        for(int i=1;i<vec.size();i++)
        {
            BST_insert(vec[0],vec[i]);
        }
        return vec[0];
    }
};

2.2.1 该题的设计思路：

序列化：层序遍历，空节点存储为#,非空节点存储值再加一个！作为分割。比如[2,1,3]，存储为"2!1!3!####"。
反序列化：也是层序构建，根据！将节点值分割出来，#则建立空节点。

• 时间复杂度：O(n)
• 空间复杂度：O(n)

2.2.2 该题的伪代码：

void num2str(int val,string& data)
    {
        定义字符串tmp
        while val不为0
            tmp+=val对10取余后转化为数字字符
            val除以10
        end while
        for 定义i从tmp的长度减到0
            data加上tmp[i]的值
        end for
        data加上字符#
    }
void BST_preorder(TreeNode*root,string& data)
    {
     if root为空
        return
     定义字符串 str_val
     num2str(root->val,str_val);
     data加上str_val的值
     BST_preorder(root->left,data);
     BST_preorder(root->right,data);
    }
void BST_insert(TreeNode* root,TreeNode* insert_node)
    {
        if root->val 大于 insert_node->val than
            if root->left不为0 than
                运行BST_insert(root->left,insert_node);
            else
                将insert_node赋值给root->right
        else
            if root->right不为0 than
                运行BST_insert(root->right,insert_node);
            else
                将insert_node赋值给root->right
    }

2.2.3 运行结果：

2.2.4 分析该题目解题优势及难点

• 对序列化和反序列化的理解
• 对树的构建

2.3 题目及解题代码

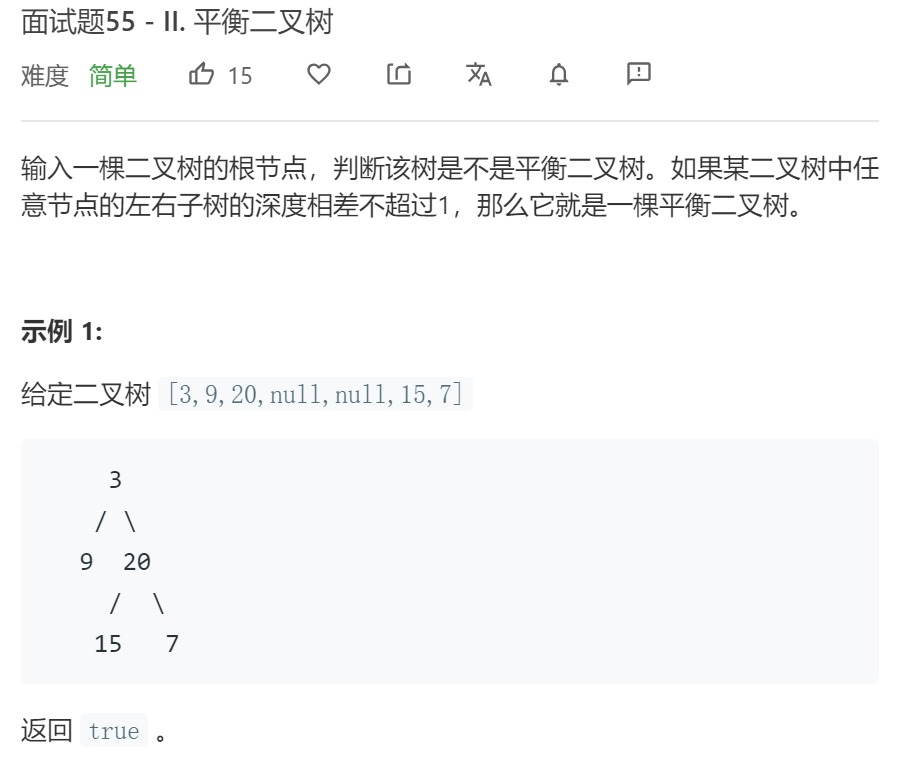
• 题目：
  
• 解题代码：

class Solution {
public:
	bool isBalanced(TreeNode* root) {
		if (root == NULL) return true;//如果该子树为空，则一定是平衡的（因为没有左右子树）
		if (abs(getHeight(root->left) - getHeight(root->right)) > 1) return false;
		return isBalanced(root->left)&& isBalanced(root->right);
	}
	int getHeight(TreeNode* root)
	{
		if (root == NULL) return 0;
		int leftHeight = getHeight(root->left);
		int rightHeight = getHeight(root->right);
		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}
};

2.3.1 该题的设计思路

先序遍历每一个节点，并比较左右子树高度，如果高度差>1则返回false

• 时间复杂度：O（n²）
• 空间复杂度：O（n）

2.3.2 该题的伪代码

bool isBalanced(TreeNode* root)
{
    if 树空 than 
        平衡
    if 左右子树高度差大于1 than 
        不平衡
    递归求取左右子树的平衡性
}
int getHeight(TreeNode* root)
{
    if 结点空 than 
        返回0
    递归求左右子树高度
    if 左子树高 than 
        返回左子树高度+1
    else （右子树高） than 
        返回右子树高度+1
}

2.3.3 运行结果

2.3.4 分析该题目解题优势及难点

• 结点平衡性的各种情况的考虑
• 解题者将题目化为左右两个子树来考虑，让读者的思维清晰了，容易理解

2.4 题目及解题代码

• 题目：
  

• 解题代码：

class Solution {
public:
    int res = 0;
    int maxlevel = 0;
    int findBottomLeftValue(TreeNode* root) {
        helper(root, 1);
        return res;
    }

    void helper(TreeNode* root, int level){
        if(root == NULL) return;

        helper(root->left, level + 1);

        if(level > maxlevel){
            maxlevel = level;
            res = root->val;
        }

        helper(root->right, level + 1);
    }
};

2.4.1 该题的设计思路:

中序遍历，使用一个全局遍量记录最大深度，当到达的深度大于目前的最大深度时，为第一次到达该最大深度，更新结果，不超过该深度时，均不会更新

• 时间复杂度：每个结点访问一次，O(n)
• 空间复杂度：不计算调栈，O(1)；计算调栈O(h)，h为最大深度

2.4.2 该题的伪代码

int findBottomLeftValue(TreeNode* root) {
    运行函数helper(root, 1);
    返回res
}
void helper(TreeNode* root, int level){
    if root为空 than
        return；
    运行函数helper(root->left, level + 1);
    if level大于maxlevel than
        将level的值赋值给maxlevel
        将root->val赋值给res
    运行函数helper(root->right, level + 1);
}

2.4.3 运行结果：

2.4.4 分析该题目解题优势及难点

• 要不断寻找，直到找到深度最大的结点
• 有利于我们对于遍历的运用
• 有利于对层次遍历的进一步掌握