The 2021 ICPC Asia Regionals Online Contest (II)

 

思路：

比赛的时候花了三个小时求了五阶导，真给我整吐了，这题其实就是个泰勒展开，但由于学了都没考过，早都忘了咋展了，以后打比赛绝对带着高数书！

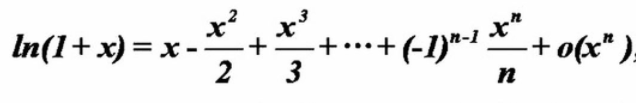
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>

using namespace std;

typedef long long LL;
typedef pair<int, int>PII;

const int N = 100010;

LL a[N], b[N];

int main()
{
    int n, t;
    cin >> n >> t;
    for (int i = 1; i <= n; i++) scanf("%lld%lld", &a[i], &b[i]);

    if (t == 0)
    {
        cout << 0;
        return 0;
    }

    for (int i = 1; i < t; i++)//看前t-1阶有没有低阶系数不是0的
    {
        LL sum = 0;
        for (int j = 1; j <= n; j++)
        {
            sum += a[j] * pow(b[j], i);
        }
        if (sum)
        {
            cout << "infinity";//如果有一次分子不是0，则为常数/0型，答案为无穷
            return 0;
        }
    }


    //到这里低阶系数必然全是0，所以只算最高阶系数
    LL suma = 0;
    for (int i = 1; i <= n; i++)
    {
        if (t % 2 == 0) a[i] *= -1;//只算最高阶，因为如果低阶有系数不是0直接就无穷了
        for (int j = 1; j <= t; j++)
        {
            a[i] *= b[i];
        }
        suma += a[i];
    }

    int k = __gcd((LL)t, abs(suma));
    t /= k;
    suma /= k;

    if (t == 1) cout << suma;
    else cout << suma << "/" << t;

    return 0;
}

 

 

 

 

思路：

 

官方题解如下：

 

 

 

 怎么说，就。。。很懵。。。我以为用随机数过题就是开玩笑的。。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int main()
{
    int k, r;
    cin >> k >> r;
    int t = (512 + r - 1) / r;//表示512/r上取整
    for(int e = 1; e <= k; e ++ )
    {
        string s(256, '0');
        for(int i = 0; i < t; i ++ ) s[rand() & 255] = '1';
        cout << s;
        if(e != k) cout << endl;
    }
    return 0;
}

 

别的大佬写的，为啥这么写也不是很懂（QWQ）

 

 

 思路：

遍历从最高的地方到最低的地方，记录每个较高的地方会流向四周的哪，即四周都有哪些格子比它低，然后比它低的格子加上的值是这个较高的格子的值除以比它低的格子的个数。给两种写法，比较推荐的是用优先队列做，因为优先队列确实要比桶好想。

1.用桶做，需要存下坐标，不知道原理，但过程看着及其丝滑

 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int>PII;

const int N = 510;

int n, m;
int h[N][N];
double g[N][N];
vector<PII>index[100010];

int main()
{
    cin >> n >> m;

    int maxh = -0x3f3f3f3f, minh = 0x3f3f3f3f;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
        {
            cin >> h[i][j];
            maxh = max(maxh, h[i][j]);//记录最高和最低的高度
            minh = min(minh, h[i][j]);
        }

    for(int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j++)
        {
            g[i][j] = m;//每个格子都有m的降水
            index[h[i][j]].push_back({ i, j });//存下标
        }

    for(int i = maxh; i > minh; i -- )
        for (auto k : index[i])
        {
            int x = k.x, y = k.y;
            int cnt = 0;//周围有多少个比他高度低的格子
            bool u = false, d = false, l = false, r = false;
            if (h[x][y] > h[x][y - 1] && y - 1 >= 1)
            {
                u = true;
                cnt++;
            }
            if (h[x][y] > h[x][y + 1] && y + 1 <= n)
            {
                d = true;
                cnt++;
            }
            if (h[x][y] > h[x - 1][y] && x - 1 >= 1)
            {
                l = true;
                cnt++;
            }
            if (h[x][y] > h[x + 1][y] && x + 1 <= n)
            {
                r = true;
                cnt++;
            }
            if (u) g[x][y - 1] += g[x][y] / cnt;
            if (d) g[x][y + 1] += g[x][y] / cnt;
            if (l) g[x - 1][y] += g[x][y] / cnt;
            if (r) g[x + 1][y] += g[x][y] / cnt;
            g[x][y] = 0;//流完了
        }

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            if (h[i][j] == 0) printf("%d ", 0);
            else printf("%.6lf ", g[i][j]);
        }

        cout << endl;
    }
    return 0;
}

 

2.优先队列bfs，因为要找最高的点和最低的点，所以可以用优先队列做，因为优先队列自动排序，我们可以开一个结构体存一个点的x，y坐标和高度h，然后定义排序的规则是按高度h从小到大排，之后我们把每个点存到优先队列里，之后最关键的问题就在于我们怎么记录一个点的四周比它低的格子的数量，并且怎样才能把它的水分配给这些格子。其实我们只需要开一个结构体类型的vector，然后枚举四个方向，如果有一个格子比当前高度低，就把它存到vector里。这个格子的四个方向枚举完之后，就遍历vector中的元素，让里面的元素的值加上（当前格子的值 除以 vector的size大小）就可以了，每个格子的值我们可以存到一个二维的res数组里。

 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int>PII;

const int N = 510;

int n, m;
int H[N][N];
double res[N][N];
int dx[] = { -1, 0, 1, 0 };
int dy[] = { 0, 1, 0, -1 };
struct Grid {
    int x, y, h;
    Grid(int a, int b, int c) {
        x = a; y = b; h = c;
    }
    bool operator<(const Grid &t)const {
        return h < t.h;
    }
};

void bfs()
{
    priority_queue<Grid>q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
        {
            cin >> H[i][j];
            res[i][j] = m;
            q.push(Grid(i, j, H[i][j]));
        }

    while (!q.empty())
    {
        auto t = q.top();
        q.pop();
        vector<Grid>g;
        for (int i = 0; i < 4; i++)
        {
            int a = t.x + dx[i], b = t.y + dy[i];
            if (a >= 1 && a <= n && b >= 1 && b <= n)
            {
                if (H[a][b] < t.h)
                    g.push_back(Grid(a, b, H[a][b]));
            }
        }

        for (int i = 0; i < g.size(); i++)
            res[g[i].x][g[i].y] += res[t.x][t.y] / (double)g.size();

    }
}

int main() 
{
    cin >> n >> m;
    
    bfs();

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
            if (H[i][j] == 0)printf("%.6lf ", res[i][j]);
            else printf("%d ", 0);

        cout << endl;
    }

    return 0;
}

 

思路：

忽略每一位的权值，我们只考虑c[i]这一位到底是0还是1，所以问题转化为从地位到高位的二进制加减。但因符号位sgn的存在，要考虑的点比较复杂，所以细节比较多。

分类讨论进位的多种情况。

 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int>PII;

const int N = 110;

int a[N], b[N], sgn[N], c[N];

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> sgn[i];
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> b[i];
    
    int fp = 0;//进位
    for (int i = 1; i <= n; i++)
    {
        fp *= sgn[i];//进位进到当前位（乘当前位的符号）
        int tmp = a[i] + b[i] + fp;
        if (tmp == 0 || tmp == 1)//没有进位
        {
            c[i] = tmp;
            fp = 0;
        }
        if (tmp == 2)//1 + 1，或1 + 进位1 -> 往前进1
        {
            c[i] = 0;
            fp = 1;
        }
        if (tmp == 3)//1 + 1 + 进位1 -> 往前进1
        {
            c[i] = 1;
            fp = 1;
        }
        if (tmp == -1)//向高位借1
        {
            c[i] = 1;
            fp = -1;
        }
        fp *= sgn[i];//当前位产生给下一位的进位（乘当前位的符号，负号就对应产生负进位）
    }

    for (int i = 1; i < n; i++) cout << c[i] << ' ';
    cout << c[n];

    return 0;
}