2021.3.7年度训练联盟热身训练赛第一场

F. Pulling Their Weight

题意：

输入n个数，分为两组，要求两组数的和相等，给定一个数t，要求t比一组的全部数大，比另一组的全部数小，找出最小的t。

tip：当t和n个数中的数有相同时，如果个数为偶数，就把他们分别分到两组，如果个数为奇数，就剔除一个，变成偶数，按偶数处理。

思路：

先排序，然后用前缀和记录对应区间的和。如果遍历到某个前缀和的2倍正好是所有数的和，那么这个前缀和对应的数+1（最小的t），就是想要的答案，

如果有两个相同元素，那就是这个前缀和对应的a值（因为偶数不会被踢）。还有当某个前缀和*2大于总和，就把这个数作为t。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

int n, a[100010], sum[100010], ans;

int main()
{
    memset(sum, 0, sizeof(sum));
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    sort(a + 1, a + n + 1);

    for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + a[i];

    for (int i = 1; i <= n; i++)
    {
        if (sum[i] * 2 > sum[n])
        {
            ans = a[i];
            break;
        }
        else if (sum[i] * 2 == sum[n])
        {
            if (a[i] == a[i + 1])
            {
                ans = a[i];
                break;
            }
            else
            {
                ans = a[i] + 1;
                break;
            }
        }
    }
    cout << ans << endl;
    return 0;
}

 

H.On Average They're Purple

 

 题意：
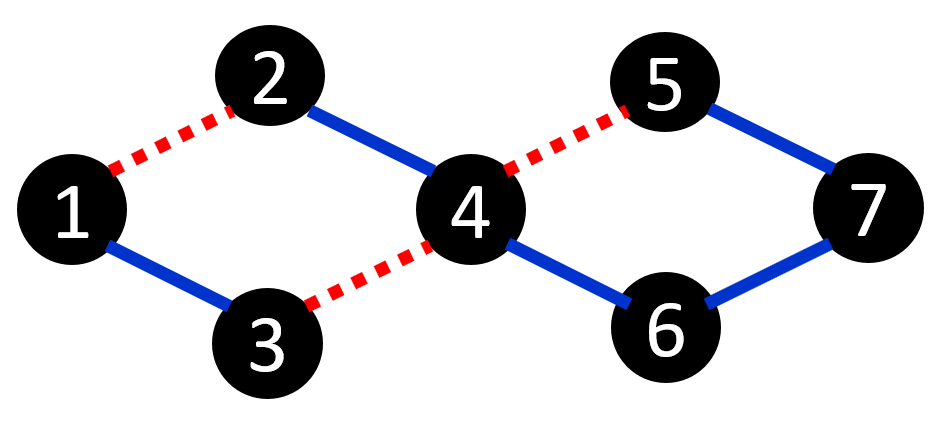
无向图，你可以给边染色，如果走过的相邻两条边颜色不同，那么权值加一。求一种染色方案，起点终点所有路径中染色得到权值的最小值最大，输出权值。

由分析得所求颜色变化数为最短路径上步数减一

 

Dijkstra + heap:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int , int>PII;

const int N = 1000010;

int n,m;
int h[N] , e[N] , ne[N] , w[N] , idx;
int dis[N];
bool st[N];

void add(int a , int b)
{
    e[idx] = b , ne[idx] = h[a] , h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dis , 0x3f , sizeof dis);
    dis[1] = 0;

    priority_queue<PII , vector<PII> , greater<PII>> heap;
    heap.push({0 , 1});//1号点距离为0 编号为1

    while(!heap.empty())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second , distance = t.first;
        if(st[ver]) continue;//ver这个点之前出现过了，是个冗余点

        st[ver] = true;

        for(int i = h[ver] ; i != -1 ; i = ne[i] )
        {
            int j = e[i];
            if(dis[j] > distance + 1)
            {
                dis[j] = distance + 1;
                heap.push({dis[j] , j});
            }
        }
    }

    return dis[n];
}

int main()
{
    cin >> n >> m;

    memset(h , -1 , sizeof h);

    while(m -- )
    {
        int a , b ;
        cin >> a >> b;
        add(a , b);//邻接表重边无所谓
        add(b , a);
    }

    cout << dijkstra() - 1 << endl;

    return 0;
}

 

Spfa:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 1000010;

int n,m;
int h[N] , e[N] , ne[N] , idx;
int dis[N];
bool st[N];

void add(int a , int b)
{
    e[idx] = b , ne[idx] = h[a] , h[a] = idx ++ ;
}

int spfa()
{
    queue<int>q;

    memset(dis , 0x3f , sizeof dis);
    dis[1] = 0;
    q.push(1);
    st[1] = true;//判断当前点是否在队列当中

    while(!q.empty())
    {
        auto t = q.front();
        q.pop();
        st[t] = false;//这个点在队列中出来了,所以置为false

        for(int i = h[t] ; i != -1 ; i = ne[i])
        {
            int j = e[i];
            if(dis[j] > dis[t] + 1)
            {
                dis[j] = dis[t] + 1;
                if(st[j] == false)//这个点不在队列当中才加到队列里
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return dis[n];
}

int main()
{
    cin >> n >> m;

    memset(h , -1 , sizeof h);

    while(m -- )
    {
        int a , b;
        cin >> a >> b;
        add(a , b);
        add(b , a);
    }

    int t = spfa();
    
    cout << t - 1 << endl;

    return 0;
}