算法的性能分析

算法耗费的时间和语句频度

时间频度：T(n)

一个算法的语句执行次数称为时间频度用T(n)表示，n表示问题的规模即执行次数

例：

for(i<n;i<n;i++){       //n+1
    for(j=0;j<n;j++){   //n+1
        c[i][j]=0		//n^2
        for(k=0;k<n;k++){	//n^2(n+1)
            c[i][j]=c[i][j]+a[j][k]*b[k][j]	//n^3
        }
    }
}
/*
该算法的频度之和为：T(n)=2n^3+3n^2+2n+1
*/

算法的时间复杂度

时间复杂度:T(n)=O(f(n)) 即 T(n)=O(n)

1. 时间复杂度的计算实际上就是算法中基本语句的执行次数的数量级。
2. 只需要计算基本语句执行次数的数量级，通俗的讲就是只要保证基本语句执行次数的函数中的最高次幂正确即可，即可以忽略所有低次幂和最高次幂的系数。这样可以简化算法分析，使其更能体现在增长率上。

时间复杂度举例：

• 时间复杂度为：O(1)

  /*
  时间复杂度为：O(1)
  */
  int count=0;
  

• 时间复杂度为：O(1)

  /*
  时间复杂度为：O(1)
  */
  int count=0;
  int count2=0;
  

• 时间复杂度为：O(n)循环语句

  /*
  时间复杂度为：O(n)循环语句
  */
  int n= 8,count=0;
  for(int i=1;i<=n;i++){
      count++;
  }
  

• 时间复杂度为：O(log2n)的循环语句

  /*
  时间复杂度为：O(log2n)的循环语句
  n在log中是真数
  */
  int n= 8,count=0;
  for(int i=1;i<=n;i*=2){
      count++;
  }
  

• 时间复杂度为：O(n^2)的二重循环

  /*
  时间复杂度为：O(n^2)的二重循环
  */
  int n= 8,count=0;
  for(int i=1;i<=n;i++){
      for(int j=1;j<=n;J++){
           count++;   
      }
  }
  

• 时间复杂度为：O(nlog2n)的二重循环

  /*
  时间复杂度为：O(nlog2n)的二重循环
  n在log中是真数
  */
  int n= 8,count=0;
  for(int i=1;i<=n;i*=2){
      for(int j=1;j<=n;J++){
           count++;   
      }
  }
  

• 时间复杂度为：O(n^2)的二重循环

  /*
  时间复杂度为：O(n^2)的二重循环
  */
  int n= 8,count=0;
  for(int i=1;i<=n;i++){
      for(int j=1;j<=i;J++){
           count++;   
      }
  }
  

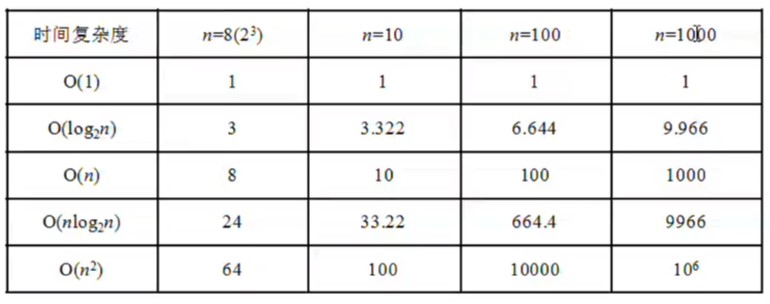
总结：时间复杂度级别

常量阶O(1)<对数阶O(log2n)<线性阶O(n)<线性对数阶O(nlog2n)<平分阶O(n^{2)<k次方阶O(n}k)<指数阶O(2^n)

即：O(1)<O(log2n)<O(n)<O(nlog2n)<O(n^2)<O(nk)<O(2^n)

注：一般情况下，随着n的增大阶T(n)增长较慢的算法为最优算法。

算法的空间复杂度

空间复杂度：S(n)=O(g(n))

1. 空间复杂度即数据所占用的空间数
2. 数据所占用的空间只取决于问题本身，和算法无关，只许分析变量所占用的额外空间

• 空间复杂度为：S(n)=O(1)

  /*
  由于算法中临时变量的个数与问题无关，所以空间复杂度为S(n)=O(1)
  */
  int i,j,k,s;
  for(i=0;i<=n;i++){
      for(j=0;j<=i;j++){
          for(k=0;k<=j;k++){
              s++;
          }
      }
  }
  

• 递归算法空间复杂度为：S(n)=O(n)，由于递归算法每次都要调用本身并要分配空间所以递归算法空间复杂度是S(n)=O(n)。